Приклад. Знайти корінь нелінійного рівнянняx3 + sin(x – 3) +1 = 0 з точністю e =0.0001

Знайти корінь нелінійного рівняння x³ + sin(x – 3) +1 = 0 з точністю e =0.0001

1 етап. Графічне відділення коренів рівняння.

1). Побудуємо графік функції f(x) = x³ + sin(x – 3) +1.

- Опишемо функцію в виді функції користувача:

- Вставимо в документ графічну область командою Insert®Graph®XY-Plot:

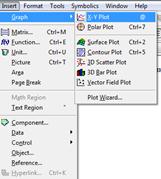
Маркери (n)отриманого шаблону заповнимо відповідно іменем аргументу х і іменем функції f(x):

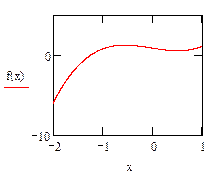
- Відформатуємо графік командою Format®Graph®XY-Plot:

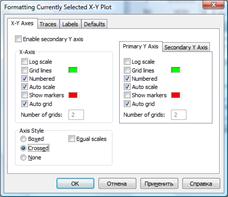
Виберемо опцію Grossed (показувати осі координат):

Як видно із графіка функція f(x) перетинає вісь абсцис на інтервалі [ -2; -1]. Для подальших розрахунків приймемо наближене значення кореня x = -1

2 етап - уточнення кореня до точністі e =0.0001.

Уточнення кореня, тобто доведення його до заданого ступеню точності e проведемо за допомогою стандартної функції root (f(x), x).

Функція реалізує обчислення ітераційним методом, причому спочатку необхідно задати:

ü точність обчислень за допомогою системної змінної TOL;

ü початкове значення змінної х (будь-яке значення з відрізку визначеного на графіку).

Порядок дій:   TOL:=0.0001	Пояснення: TOL - системна змінна, за допомогою якої задається точність обчислень в системі MathCAD.
x:= -1	Початкова умова, знайдена із графіка.   Описуємо функцію f(x), як функцію користувача.
x:= root(f(x), x) x= - 1.2361	Застосування функції rootдля уточнення кореня. Вивід значенння уточненого кореня х. В установленому режимі MathCAD як правило виводить 3 десяткові знаки після коми. Оскільки задана точність e потребує 4 знаки, необхідно командою Format®Result… в вікні Result Format задати необхідне число знаків: 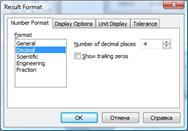    Отже корінь рівняння х= -1,236.

Вирішення систем нелінійних рівнянь.

Дана система двох рівнянь з двома невідомими

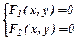, де F1 і F2 нелінійні функції.

Потрібно знайти дійсні корені ( значення х0 і у0, які перетворюють обидва рівняння системи на тотожність ) з заданим ступенем точності e.

Для вирішення системи в MathCad необхідно знати початкові (наближені значення х0 і у0).

Для знаходження початкових значень х0 і у0 виконують настурні дії:

ü Приводять систему до вигляду

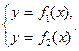- еквівалентна система.

ü Будують графіки функцій f₁(х) і f₂(х), на яких можна визначити початкові (наближені) значення розв’язку як точки перетину цих графіків.

При уточненні кореня до заданої точності e у системі MathCad використовується спеціальний обчислювальний блок, що має наступну структуру:

· Директива Given – відкриває блок;

· За нею слідують рівняння;

· Закриває блок функція Find, яка проводить уточнення розв’язку.

Функція Find (х1,х2... хn) повертає одній або ряду змінних їх уточненені значення.

Дата добавления: 2014-01-04