Приклад. Розв’язати систему нелінійних рівнянь:

Постановка задачі.

Розв’язати систему нелінійних рівнянь:

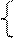sin(x) + sin(y)-1.3 = 0,

y² –x² +x = 0.

с точністю e=0.00001.

Відомо, що розв’язком системи є такі значення х і у, які перетворюють одночасно обидва рівняння в тотожності.

Для знаходження розв’язку системи необхідно спочатку графічно знайти грубе наближення цих значень для х і у.

Очевидно, що потрібно побудувати криві, які описуються рівняннями системи. Координати точки перетину цих кривих (як спільна їх точка) і являтимуться розв’язком системи.

Щоб побудувати ці криві необхідно рівняння системи привести до виду (у виразити черех х):

y = f1(x)

y = f2(x),

тобто в нашому випадку:

.

Після цього побудувати графіки функцій:

.

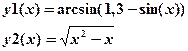Порядок дій:	Пояснення:
1.Описуємо дві функції користувача	Функції asin, sin і Ö вибрати з панелі Calculator.
2.Будуємо графіки функцій: y1(x) і y2(x)
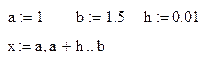
	Довільно вибираємо відрізок [a,b], на якому будуємо графік функцій. Задаємо розбиття відрізку точками, описавши х як ранжовану змінну, яка змінюватиметься від а до в з кроком h. Якщо на вибраному відрізку [a,b]криві не перетнуться змінюємо до тих пір а і в поки не віднайдемо точку перетину.
	Із графіка приблизно знайти значення: х=1,2 і у = 0,4 координати точки перетинання графіків
3.Задаємо початкові значення розвязку: x:=1.2 y: = 0.4	Задаємо початкові значення для х і у.
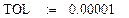
	Задаємо точність обчислень
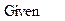
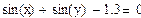
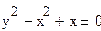
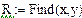
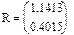
4.Уточнюємо розвязок до задоного ступеня точності.	Для уточнення розвязку використовуємо блок рішення, який відкривається директивою Given, а закривається функцією Find. В самому блоці записуються рівняння системи, в яких знак = вставляється з панелі . Вектору R присвоюється рішення системи. Отже х = 1,1413 і у = 0,4015.
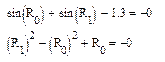
5.Проводимо перевірку розвязку:	Перевірка розвязку: Замість х і у підставляємо в рівняння R0 і R1, які являються елементами вектора R(нумерація елементів починається з нуля). Оскільки справа отримали нулі – розвязок задовільняє обидва рівняння.

Лекція №6

Тема: Розв’язання задаx оптимізації.

План:

1. Задача одновимірної оптимізації і її рішення.
2. Задача багатовимірної оптимізації і її рішення.

Завдання оптимізації.

Основною метою вирішення завдань управління системою є досягнення деякого оптимального режиму роботи. Багато досліджуваних процесів вимагають оптимізації. Під оптимізацією мають на увазі знаходження max або min функції. Завдання оптимізації діляться на:

G - завдання одновимірної оптимізації

G - завдання багатовимірної оптимізації.

Одновимірна оптимізація розглядає функції, залежні від однієї змінної.

Багатовимірна оптимізація розглядає функції, залежні від багатьох змінних.

Задача одновимірної оптимізації.

Постановка завдання:

Дана функція y=f(x)

Потрібно визначити мінімальне значення функції min f(x)

Методи мінімізації дозволяють визначити точку мінімуму функції, тобто таке значення x*, при якому функція досягає min значення. f_min=((x*). При цьому задається точність, яка визначає наближене значення точки мінімуму функції.

Ця задача розвязується в два етапи:

1. Графічним методом проводиться пошук початкового значення точки мінімума.

Для цього необхідно побудувати графік функції f(x).

Проаналізувати чи має вона мінімум і, якщо так,

то з графіку наближено визначити при якому значенні аргументу х

цей мінімум досягається.

2. Потім початкове значення точки мінімума уточнюється до заданого ступена точності e.

У MathCad цю задачу можна вирішити за допомогою вирішального блоку. У тілі блоку записуємо необхідну умову екстремуму функції, що диференціюється.

Дата добавления: 2014-01-04