Лекция №3

; ; ;

; ; ; ; ;

;

; ; ; ; ; ;

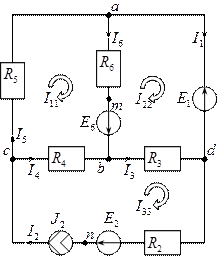
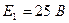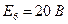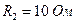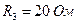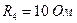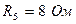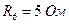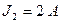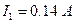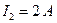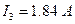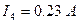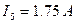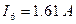Метод контурных токов:

;

;

;

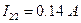Теперь через контурные токи выражаем токи в ветвях:

;

;

;

;

.

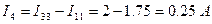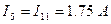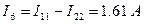Если в схеме есть 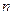независимых контуров, то система уравнений будет выглядеть следующим образом: . Если какой-либо контурный ток известен, то уравнение для него не пишут, но в остальных уравнениях его учитывают.

Преобразование схемы типа «звезда» в схему типа «треугольник».

В узлах 1, 2, 3 и схема типа «звезда» и схема типа «треугольник» соединяются с остальной частью цепи. Часто есть необходимость преобразовать схему типа «звезда» в схему типа «треугольник» или наоборот схему типа «треугольник» в схему типа «звезда». Если преобразование выполнить так, что при одинаковых значениях потенциалов узлов, подтекающие к ним токи одинаковы, то на внешней цепи эта замена не отразится.

Переход от схемы типа «Звезда» к схеме типа «Треугольник» осуществляется по следующим формулам: ; ; .

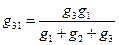Пример:

Обратный переход от схемы типа «Треугольник» к схеме типа «Звезда» осуществляется следующим образом:

;

;

;

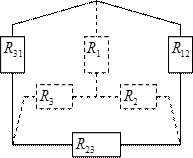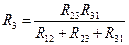Метод эквивалентного генератора.

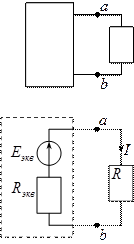В любой электрической цепи можно выделить какую-то одну ветвь, а всю основную схему условно изобразить в виде прямоугольника. По отношению к выделенной ветви вся схема будет представлять собой двухполюсник.

Если в двухполюснике есть источник ЭДС или источник тока, то он называется активным, в противном случае он называется пассивным.

Доказано, что активный двухполюсник можно представить, как эквивалентный генератор с параметрами и , причём равно напряжению холостого хода на зажимах ветви 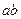, то есть 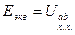, а равно входному сопротивлению двухполюсника по отношению к точкам 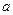и 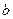с учётом сопротивлений источников, то есть .

Ток выделенной ветви можно найти по закону Ома: .

Этот метод применяется для расчёта тока в какой-то одной ветви электрической цепи.

Алгоритм расчёта:

1. Разрываем ветвь, в которой ищем ток, то есть создаём режим холостого хода, и определяем напряжение на зажимах оборванной ветви, то есть определяем .

2. Определяем , при этом закорачиваем источники ЭДС и разрываем ветви с источниками тока, что бы учесть внутреннее сопротивление источников тока.

3. Определяем ток выделенной ветви по закону Ома: .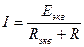

Пример:

Дано:

.

; ; ; ; ; .

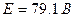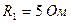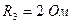Задание определить ток 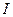методом эквивалентного генератора.

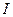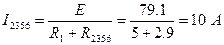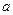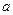1. Обрываем ветку, в которой ищем ток . Тогда . Находим ток: . Воспользуемся методом разброса токов: ; . Потенциал точки : , тогда разность потенциалов между точками и 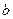: . Следовательно, напряжение холостого хода на зажимах ветви 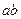: . Поэтому .

2. Определяем , учитывая сопротивление источников. Для этого требуется преобразовать верхнюю схему типа «треугольник» в схему типа «звез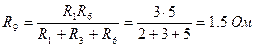да»: ; ; . Тогда , следовательно .

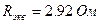3. Определяем ток по закону Ома: .

Передача энергии от активного двухполюсника к нагрузке.

Пользуясь методом эквивалентного генератора, найдём текущий через нагрузку ток: 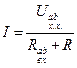. Полезную мощность можно найти по формуле: . Для того, чтобы выяснить при каких условиях в нагрузке будет выделяться максимальная мощность, берётся производная 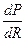, приравнивается к нулю и получается, что - условие выделения максимальной мощности на нагрузке. Тогда .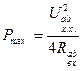

Определим коэффициент полезного действия: . Полную мощность можно найти по формуле: 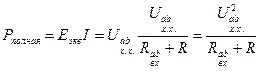, тогда коэффициент полезного действия: . Видно, что коэффициент полезного действия зависит от соотношения сопротивлений нагрузки и входного сопротивления двухполюсника. Если они равны то . Выбор сопротивление нагрузки равным входному сопротивлению двухполюсника называется согласованием нагрузки.

Пример:

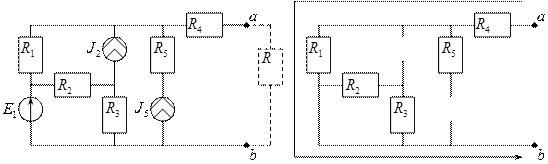
Задание: определить, каким должно быть сопротивление нагрузки, что бы в ней выделялась максимальная мощность.

Для того, чтобы в нагрузке выделялась максимальная мощность, необходимо, чтобы . Проследим путь тока от точки 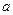до точки 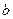: 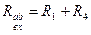. Следовательно, сопротивление нагрузки: .

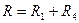Дата добавления: 2014-01-04