Лекция №7

Передача энергии от активного двухполюсника к нагрузке.

Найдёт ток по методу эквивалентного генератора:

.

Выясним, при каких условиях в нагрузке будет выделяться максимальная мощность. Внутренние активные и реактивные сопротивления и 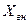изменить нельзя, так как это параметры самой цепи. Если реактивное сопротивление нагрузки 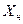подобрать равным реактивному внутреннему сопротивлению 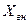, то двухполюсник будет работать в резонансном режиме и ток 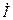, текущий через нагрузку будет совпадать по фазе с напряжением 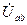, то есть .

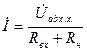Так как же в цепи постоянного тока максимальная мощность 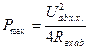выделятся в случае, когда активное сопротивление нагрузки равно активному внутреннему сопротивлению двухполюсника .

Таким образом, существует два условия выделения максимальной мощности на нагрузке: и .

Трёхфазные цепи.

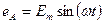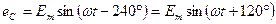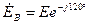Трёхфазная симметричная система ЭДС – совокупность трёх синусоидальных ЭДС одинаковой частоты и амплитуды, но сдвинутых на 120 градусов друг от друга, то есть ; ; , или ; ; , где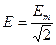

Трёхфазная цепь – совокупность трёхфазной системы ЭДС, трёхфазной нагрузки и соединительных проводов.

В подавляющем большинстве случаев для передачи энергии используются трёхфазные цепи.

Так как векторная сумма ЭДС равна нулю, то в случае, если нагрузка не присоединена к зажимам 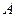, , 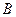, 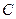то по обмоткам генератора ток протекать не будет.

Трёхфазного источника в цепях обозначается следующим образом:

Существует пять простейших способов соединения трёхфазного генератора с трёхфазной нагрузкой:

1. «Звезда-звезда» с нулевым проводом.

2. «Звезда-звезда» без нулевого провода.

3. «Звезда-треугольник»

4. «Треугольник-треугольник».

5. 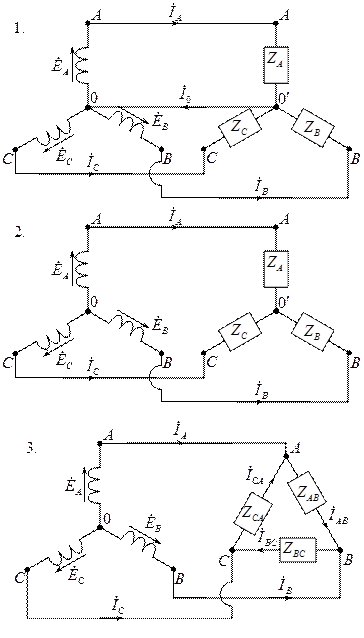«Треугольник-звезда»

Нулевой провод – провод, соединяющий нулевые точки генератора и нагрузки.

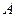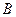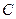Линейные провода – провода, соединяющие точки , и генератора и нагрузки.

Линейные токи – токи, текущие через линейные провода.

Линейные напряжения – напряжения между линейными проводами.

Фаза генератора – каждая и трёх обмоток генератора.

Фаза нагрузки – каждая из трёх нагрузок.

Фазовые токи – токи, протекающие через фазы генератора и нагрузки.

Фазовые напряжения – напряжения на фазах генератора и нагрузки.

При присоединении трёхфазного генератора «звездой» линейное напряжение по модулю в 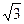больше фазного.

;

;

;

;

;

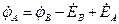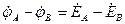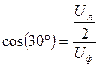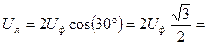
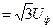Линейные напряжения:

;

;

.

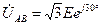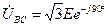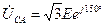При присоединении генератора «треугольником» линейное напряжение равно фазовому, то есть .

При присоединении нагрузки «треугольником» положительное направление токов выбирают по часовой стрелке, при этом линейные токи не равны фазовым. Но линейные токи можно найти с помощью фазовых, используя первый закон Кирхгофа.

Расчёт трёхфазных цепей.

Так как трёхфазовые цепи являются разновидностью цепей синусоидального тока, то расчёт и исследование их проводят с помощью тех же методов. Возможно применение так же символического метода. Кроме того, аналитический расчёт следует сопровождать построением векторных диаграмм.

Рассмотрим схему типа «звезда-звезда» с нулевым проводом.

Если нулевой провод обладает малым сопротивлением, то потенциал точки 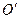можно считать равным потенциалу точки 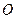, то есть нулевой провод можно закоротить и схема преобразуется в три независимых контура.

Токи в этих контурах можно найти по следующим формулам: 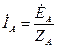; ; 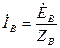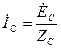. Ток, текущий через нулевой провод можно найти по первому закону Кирхгофа: 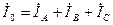. В случае равномерной (симметричной) нагрузки, при которой выполняется условие 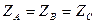, нулевой ток равен нулю.

Допустим, что сопротивление нагрузок равны, то есть 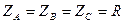. В этом случае токи, текущие через линейный провода можно найти по следующим формулам: , , .

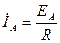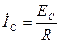Нулевой провод может быть изъят из цепи без изменения её работы.

Построим векторную диаграмму.

При неравномерной нагрузке фаз нулевой ток уже не будет равен нулю.

При наличии в нулевом проводе сопротивления расчёт производится методом двух узлов.

Рассмотрим случай неравномерной нагрузки.

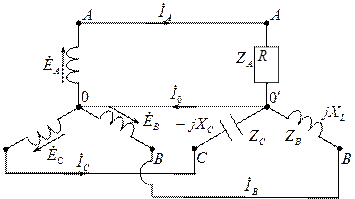
Дано:

;

; ; .

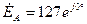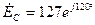Аналитический способ решения:

; ; .

;

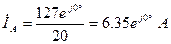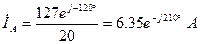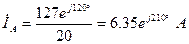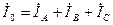Геометрический метод решения с помощью векторных диаграмм:

;

.

Дата добавления: 2014-01-04