Оператор примитивной рекурсии

Оператор суперпозиции.

Рекурсивные функции

Договоримся, что в этом параграфе

1. множество N натуральных чисел содержит 0 (нуль), т.е. N={0,1,2,3,...};

2. рассматриваемые функции f=f(x₁,x₂,...,x_n) определены только тогда, когда переменные принимают значения из N,

т.е. x_iÎN;

3. область значений функций DÍN;

4. рассматриваемые функции f=f(x₁,x₂,...,x_n) могут быть частично определенные, т.е. определенные не для всех наборов натуральных чисел.

Введём в рассмотрение простейшие функции

o(x)=0, s(x)=x+l, Im n(х1,...,хn) = xm

Эти функции могут быть вычислены с помощью соответствующего механического устройства (например, на машине Тьюринга). Определим операторы, которые по одной или нескольким заданным функциям строят новые функции.

Пусть даны функция f(x₁,x₂,...,x_k) от k переменных и k функций f1(x₁,x₂,...,x_n),...,f_k (x₁,x₂,...,x_n) от n переменных. Суперпозицией функций f,f₁...,f_k называется функция

y (х1,x2,...,xn)= f(f1(x1,x2,...,xn),...,fk(x1,x2,...,xn))

Мы говорим, что функция y получается применением оператора суперпозиции S^K+I к функциям f,f₁...,f_k, и пишем y=S^K+1(f,f₁,...,f_k)

Например, S²(s,o)=s(o(x)), т.е. функция, тождественно равная 1, а S²(s,s)=s(s(x)) - это функция у(х)=х+2.

Пусть даны функции g(x₁,x₂,...,x_n) и h(x₁,x₂,...,x_n+2). Построим функцию f(x₁,x₂,...,x_n+1) Пусть зафиксированы значения x₁,x₂,...,x_n. Тогда полагаем:

f(x₁,x₂,...,x_n,0)= g(x₁,x₂,...,x_n)

f1(x₁,x₂,...,x_n,у+1)= h(x₁,x₂,...,x_n,у, f(x₁,x₂,...,x_n,y))

Эти равенства определяют функцию f(x₁,x₂,...,x_n+1) однозначно. Функция f называется функцией, полученной с помощью оператора R примитивной рекурсии. Используется запись f=R(g,h).

Индуктивное определение функции (продемонстрированное в операторе примитивной рекурсии) в математике не редкость. Например, индуктивно определяются 1) степень с натуральным показателем: а⁰= 1,

а^п+1=аⁿа;

2) факториал: 0! = 1, (n+l)! = n!(n+1) и т.д.

Определение. Функции, которые могут быть получены из простейших о(х)=0, s(x)=x + 1, I^m _n(х₁,...,х_n) = x_m применением конечного числа раз операторов суперпозиции и примитивной рекурсии, называются примитивно рекурсивными.

Проверим, что функция u(х,у)=х+у является примитивно рекурсивной. Действительно, мы имеем: u(x,0)=0, u(x,y+l)=х+у+1=u(х,у)+1. Это есть схема примитивной рекурсии, так как x=I¹ ₁ (x), a u(x,y)+l=s(u(x,y))=S²(s,u). Здесь g(x)= I¹ ₁ (x), а

h(x,y,u)=s(u)=S²(s, I ³ ₃).

Аналогично доказывается, что функции m(x,y)=xy, d(x,y)=x^y (считаем по определению 0°=1), fact(x)=x! и многие другие являются примитивно рекурсивными.

Отметим; что примитивно рекурсивные функции всюду определены (т.е. определены для всех значений их аргументов).

Действительно, простейшие функции о, s, I^m_n являются всюду определёнными, а применение операторов суперпозиции и примитивной рекурсии ко всюду определённым функциям даёт также всюду определённые функции. Значит, такая функция, как

f(x,y)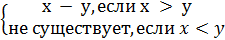

примитивно рекурсивной быть не может. Рассматривать функцию f(x,y)=x-y здесь мы не имеем права, так как значения функций должны быть натуральными числами (поэтому не отрицательными).

Однако, можно рассмотреть функцию

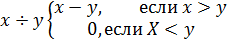
Проверим, что она примитивно рекурсивна. Докажем вначале, что функция y(х)=х-1 примитивно рекурсивна. Действительно, y(0)=0. y(у+1)=(у+1)-1=у, что служит схемой примитивной рекурсии для функции х-1 Наконец, x-0=x, х (у+1)=(х-у)- 1=y(х-у) - схема примитивной рекурсии для х-у.

Существенно более широким классом функций, чем примитивно рекурсивные функции, является класс рекурсивных функций. В литературе эти функции называют также частично рекурсивными. Для их определения введём ещё один оператор.

Задания для самостоятельной работы по теме 4.

1) Построить машину Тьюринга, которая:

1. у каждого слова длины ³ 3 в алфавите А стирает три последних символа, а слова меньшей длины перерабатывает в пустое слово.

2. приписывает к каждому слову в алфавите А слово а2а1а2 справа(слева)

3. удваивает каждое слово, т.е вычисляет функцию f(x)=xx

2. распознает, является ли слово симметричным.

3. распознает четность длины слова.

4. распознает, является ли слово х началом слова у.

2) Построить машину Тьюринга, которая распознает:

1. 1. дает ли длина слова при делении на 3 остаток 2.

2. 2. содержит ли слово заданную букву.

3. 3. имеет ли слово вид хх.

4. 4. выполняется неравенство

5. 5. совпадают ли х и у

3) Выяснить, являются ли тупиковыми или минимальными следующие ДНФ:

1. ;

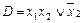2. ;

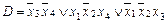3. .

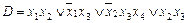4) Построить машину Тьюринга, вычисляющую:

1. наибольшее общее начало слов х и у

2. сумму двух натуральных чисел. Замечание: число задается количеством палочек в ячейках.

3. произведение двух чисел.

4. разность m-n

5. остаток от деления m на n

5) Выяснить, какие из ниже перечисленных выражений являются формулами над множеством связок {ù,&,Ú,®}:

1. x®y; 4) (x®y)®ùx; 7) (ùx®z);

2. (x&)ùz; 5) (x&yy)ùy; 8) (x®(y&(ùx)));

3. (x®y)ùx; 6) y&(z®(xÚùy)).

6) Построить таблицу функций, реализуемых следующими формулами:

1.

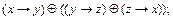
2.

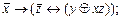
3.

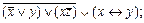
4.

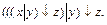
7) Получить булевы формулы для функций:

1. ,

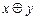2. ,

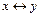3. .

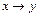Дата добавления: 2014-01-04