Указания к решению задачи. А. Вычисление расчетного расхода при достаточной продолжительности наблюдений

А. Вычисление расчетного расхода при достаточной продолжительности наблюдений

1. Определить статистические характеристики гидрологического ряда наблюдений за стоком воды в реке А.

2. Построить эмпирическую и теоретические (аналитические) кривые обеспеченности максимальных расходов воды.

3. Вычислить максимальный расход воды 1% вероятности превышения (обеспеченности) методами моментов и наибольшего правдоподобия.

Поведение случайных величин, которые составляют заданный гидрологический ряд наблюдений, можно охарактеризовать тремя параметрами:

- средним арифметическим значением;

- коэффициентом вариации;

- коэффициентом асимметрии.

Среднее арифметическое значение ряда:

(1)

где: Q_i – максимальный расход весеннего половодья, м³/с;

n – количество членов ряда.

Коэффициенты вариации и асимметрии определяются в соответствии с СП 33-101-2003 методами моментов и наибольшего правдоподобия.

1. Метод моментов. Коэффициент вариации С_v характеризует меру изменчивости членов ряда относительно среднего арифметического значения и определяется по формуле (при С_v < 0.6):

, (2)

где K_i – частное от деления i -го члена ряда на среднее арифметическое этого ряда, т.е. .

Коэффициент асимметрии С_s характеризует отличие по величине и количеству положительных (больше средних) и отрицательных (меньше средних) отклонений от среднего арифметического значения ряда. Для симметричных рядов (нормальное распределение ежегодных вероятностей превышения значений ряда) эти отклонения повторяются одинаково часто, поэтому C_s = 0. Для несимметричных рядов C_s ≠ 0, а коэффициент асимметрии определяется по формуле (при С_s < 1,0):

(3)

Расчеты по определению статистических характеристик сводятся в табл. 1. В верхней строке этой таблицы указана точность, с которой необходимо определить соответствующие величины.

Для проверки правильности определения среднего значения сравниваем суммы положительных и отрицательных значений ∑(K_i - 1). Они должны отличаться один от другого не более чем на 5%.

2. Метод наибольшего правдоподобия. Для оценки коэффициентов вариации и асимметрии этим методом необходимо предварительно определить величины статистик:

(4)

Результаты расчета, необходимые для определения этих статистик, сводятся в табл. 1. По рассчитанным значениям статистик по одной из номограмм (прил. 2) определяют характеристики ряда: C_v, C_s/C_v и C_s.

3. После определения параметров статистического ряда этими методами, по таблицам прил. 3 находятся ординаты (модульные коэффициенты) теоретической (аналитической) кривой трехпараметрического гамма-распределения ежегодных вероятностей превышения значений гидрологической характеристики или кривой обеспеченности. По ним вычисляем максимальные расходы воды заданной обеспеченности Q_р% = К_р% * Q _ср (табл. 2).

4. В задаче требуется построить эмпирическую и теоретические кривые обеспеченности.

Эмпирическую обеспеченность или ежегодную вероятность превышения гидрологических характеристик определяют по формуле:

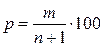, % (5)

где m – порядковый номер члена ряда, выстроенного в убывающем порядке (табл. 1).

Результаты расчета эмпирической обеспеченности приведены в табл. 1.

5. На клетчатке вероятности (рис. 1) по данным табл.1 и 2 строим:

- эмпирическую кривую обеспеченности;

- теоретическую кривую обеспеченности (метод моментов);

- теоретическую кривую обеспеченности (метод наибольшего правдоподобия).

Дата добавления: 2014-01-04