Понятия о картографической проекции и сетке

Под картографической проекцией понимается математически определен­ное отображение поверхности эллипсоида или шара (глобуса) на плоскость карты.

При этом выполняются следующие требования:

- точке, взятой на поверхности, соответствует одна и только одна точка на плоскости и наоборот;

- бесконечно малому перемещению точки на поверхности соответствует также бесконечно малое перемещение точки на плоскости и наоборот;

- сохраняется направление обхода контуров на поверхности и на плоскости.

Соответствие между точками поверхности эллипсоида (сферы) и плоскости может быть задано уравнениями вида:

(1)

где f₁ и f₂ – функции, выраженные математическими зависимостями и имеют Якобиан – определитель системы (1) –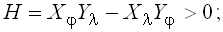

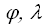– координаты точки на поверхности эллипсоида;

X, Y – координаты точки на плоскости.

Такой системой двух уравнений может быть представлена любая картографическая проекция. Но вид функции (1) может быть разнообразным в зависимости от принятых систем координат на поверхности эллипсоида вращения (сферы).

Чаще всего для описания проекций пользуются следующими характеристиками: m, n, p, ω, θ, a, b, γ:

m – масштаб длин по меридиану;

n – масштаб длин по параллели;

p – масштаб площади;

ω – наибольшее угловое искажение;

θ – угол между меридианом и параллелью;

a, b – экстремальные масштабы;

γ – сближение меридианов.

Поверхность земного шара нельзя развернуть на плоскость карты без искажений.

· искажения длин

· искажения площадей- уклонение масштаба площади от единицы, т.е. p-1

· искажения углов- удвоенное наибольшее искажение направлений, т.е. 2w

· искажения форм

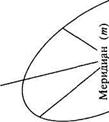
Любая бесконечно малая окружность на шаре (эллипсоиде) предстает на карте бесконечно малым эллипсом — его называют э ллипсом искажений (индикатриса). Для наглядности вместо бесконечно малого эллипса обычно рассматривают эллипс конечных размеров (рис. 3.4). Его размеры и форма отражают искажения длин, площадей и углов, а ориентировка большой оси относительно меридиана и параллели — направление наибольшего растяжения. Большая ось эллипса искажений характеризует наибольшее растяжение в данной точке, а малая ось — наибольшее сжатие, отрезки вдоль меридиана и параллели соответственно характеризуют частные масштабы по меридиану m и параллели n.

Рис. Эллипс искажений, характеризующий искажения масштабов в данной точке (в центре эллипса).

а— направление наибольшего растяжения масштаба; Ь— направление наи­большего сжатия масштаба; т — масштаб по меридиану; п — масштаб по параллели.

Значения т, п, a, b и р измеряют в процентах или в долях от главного масштаба

В ряде проекций существуют линии и точки, где искажения отсутствуют и сохраняется главный масштаб карты — это линии и точки нулевых искажений. Для наиболее употребительных проек­ций существуют специальные вспомогательные карты, на которых показаны эти линии и точки, а кроме того проведены изоколы - линии равных искажений длин, площадей, углов или форм.

Картографическая сетка — это изображение на карте линий меридианов и параллелей (географической сетки), отражающих значения долгот, счет которых ведется от начального Гринвичско­го меридиана, и широт, которые отсчитываются от экватора.

- Сетка прямоугольных координат (прямоугольная сетка) — стандартная система взаимно перпендикулярных линий, проведенных через равные расстояния, например через определенное число километров (отсюда название километровая сетка).

- Сетка-указательница — любая сетка на карте, предназначена[ для указания местоположения и поиска объектов. Ячейки такой сетки обозначаются буквами и цифрами (допустим, В-3), это удобно для отыскания объектов по их названиям.

Дата добавления: 2014-01-04