
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Закон Кулона. Экспериментальные проверки закона Кулона. Теорема Остроградского-Гаусса. Дифференциальная формулировка закона Кулона
|
|
|
|
Аудиторський висновок при виконанні завдань з аудиту спеціального призначення.
Модифікація висновку незалежного аудитора.
Модифіковані висновки - це такі висновки, що мають не безумовно-позитивне висловлення думки аудитора, тобто висновки, відмінні від безумовно-позитивних.
МСА 701 "Модифікація висновку незалежного аудитора" встановлює стандарти та надає рекомендації щодо модифікацій висновку (пояснювального параграфу, умовно-позитивного висновку, відмови від висловлення думки, негативного висновку).
Текст аудиторського висновку модифікується для таких випадків, як:
1. Питання, що не впливають на думку аудитора:(пояснюючий параграф
2. Питання, що впливають на думку аудитора: умовно-позитивна думка; відмова від висловлення думки;негативна думка.
Виконання завдань з аудиту спеціального призначення регулюється МСА 800 "Аудиторський висновок при виконанні завдань з аудиту спеціального призначення".
До завдань з аудиту спеціального призначення відносяться завдання з аудиту:
· повного пакету фінансових звітів, складених відповідно до іншої всеохопної основи бухгалтерського обліку;
· компоненту повного пакету фінансових звітів загального або спеціального призначення, наприклад, окремого фінансового звіту, конкретних рахунків, елементів рахунків або статей у фінансовому звіті
· виконання контрактних угод;
· узагальнених фінансових звітів.
Перед тим, як почати виконувати аудиторське завдання спеціального призначення, аудитор повинен переконатись, що угода із замовником визначає точний характер завдання, а також форму і зміст висновку, який буде наданий.
Плануючи аудиторську роботу, аудитор повинен чітко розуміти мету використання інформації, що міститься у висновку, а також те, хто, ймовірно користуватиметься цією інформацією. Щоб уникнути використання аудиторського висновку в непередбачених цілях, аудитор може зазначити у висновку, з якою метою він надається, і викласти будь-які обмеження щодо його розповсюдження та використання.
Аудиторський висновок при виконанні завдань з аудиту спеціального призначення має стандартну структуру (за винятком висновку про узагальнені фінансові звіти).
В аудиторському висновку доцільно зазначити мету, з якою він надається та обмеження щодо його розповсюдження та використання (для уникнення використання його в непередбачених цілях).
Закон Кулона. Кулон – 1785 – сила взаимодействия – закон:
Точечные заряды q1 и q2, помещенные в однородную изотропную среду, взаимодействуют друг с другом с силой

(2)
где k - постоянная вид, которой зависит от выбора системы отсчета, в системе СИ  (k = 1 Гауссова система); ε0 — электрическая постоянная; ε — относительная диэлектрическая проницаемость вещества (e ³ 1, eводы = 81).
(k = 1 Гауссова система); ε0 — электрическая постоянная; ε — относительная диэлектрическая проницаемость вещества (e ³ 1, eводы = 81).
Справедливость закона Кулона предполагает следующие допущения:
- только точечные заряды (Точечный заряд – физическая модель заряженного тела, размеры которого весьма малы по сравнению с расстоянием до других зарядов)
- изотропность среды (свойства среды в окрестностях любой точки одинаковы по всем направлениям)
- однородность среды
- безграничность среды
Кулон исследовал угол закручивания нити от силы (работал в области механики). Используя свой прибор, изображенный на рисунке
Прибор – крутильные весы, состоит из: стеклянного коромысла, серебряной нити  ,
, 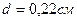 , шарика
, шарика 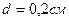 (шарик заряжают стеклянной палочкой), неподвижного шарика (его тоже заряжают).
(шарик заряжают стеклянной палочкой), неподвижного шарика (его тоже заряжают).
 |
Шарики отталкиваются, нить закручивается на угол j. Кулон установил, что сила притяжения (отталкивания) шаров пропорциональна произведению зарядов шаров и обратно пропорциональна квадрату расстояния между ними:
 ;
;
Теорема Гаусса.
Вычисление электрического поля в некоторых случая, обладающих специальной симметрией, упрощается применением теоремы Остроградского – Гаусса.
Электростатическая теор. Гаусса устан. матем. связь между потоком вектора напряженности E сквозь замкнутую поверхность S и зарядом, находящимся в объеме, ограниченной этой поверхностью.
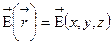 (стационарн.)
(стационарн.)
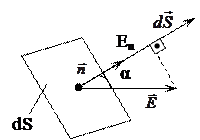 Рис. 7
Рис. 7
|
а) элементарный поток 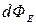 вектора
вектора  через ориентиров. плоскую элементарную площадку dS (
через ориентиров. плоскую элементарную площадку dS (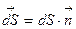 ) есть скалярная физ. величина, равная скалярному произведению
) есть скалярная физ. величина, равная скалярному произведению  на
на 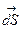 (Рис. 7):
(Рис. 7):
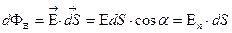 (9)
(9)
где Еп— проекция вектора  на нормаль
на нормаль 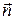 к площадке
к площадке  . Выбор направления вектора
. Выбор направления вектора 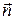 (а следовательно, и
(а следовательно, и  ) условен, его можно было направить и в противоположную сторону.
) условен, его можно было направить и в противоположную сторону.
Замечание:
Площадка элементарная, т.е. в пределах нее вектор  постоянен.
постоянен.
б) Рассмотрим поверхность S. Разобьем ее на элементарные площадки dS в пределах которых вектор  . Поток вект. поля напр. через поверхн. S есть сумма элементарных потоков
. Поток вект. поля напр. через поверхн. S есть сумма элементарных потоков 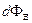 по всем элементарным площадкам dS из которых состоит поверхность S
по всем элементарным площадкам dS из которых состоит поверхность S
 (10)
(10)
Эта величина алгебраическая. Она зависит не только от конфигурации поля E, но и от выбора нормали поверхн.
Замечание: Если поверхн. S – замкн, то этот факт изображ ® 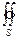 , а нормаль и к поверх. берется внешняя (наружу области, охватываемой поверхностью)
, а нормаль и к поверх. берется внешняя (наружу области, охватываемой поверхностью)
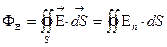
. Теорема Гаусса в дифференциальной форме.
Она устанавливает связь между объемной плотностью заряда r и изменениями напряженности поля 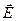 в окрестности данной точки пространства.
в окрестности данной точки пространства.
Введем дифференц. скалярную характеристику для данной точки векторного поля 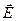 – дивергенция поля
– дивергенция поля  (div
(div ).
).
 .
.
Из математики – теорема Остроградского
 Þ т. Гаусса
Þ т. Гаусса

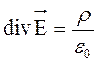
 - Т.Г в дифференц. форме или дифференц. формулировка закона Кулона.
- Т.Г в дифференц. форме или дифференц. формулировка закона Кулона.
Замечание 1:
Выражение для дивергенции зависит от выбора системы координат
- декарт: 

- цилиндр: 
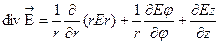 .
.
Замечание 2:
Написание формулы упрощается, если ввести векторный
 дифф. оператор
дифф. оператор (набла), приобретающий смысл в сочетании со скалярной или векторной функцией
(набла), приобретающий смысл в сочетании со скалярной или векторной функцией
 =
= 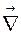 ×
× 
декарт Þ 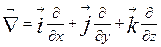 .
.
Замечание 3:
В тех точках поля, где div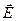 >0 имеются источники поля (полож. заряды), а где div
>0 имеются источники поля (полож. заряды), а где div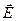 <0 имеются стоки поля (отр. Зар.). Линии
<0 имеются стоки поля (отр. Зар.). Линии  выходят из источников и заканчиваются в стоках.
выходят из источников и заканчиваются в стоках.
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 942; Нарушение авторских прав?; Мы поможем в написании вашей работы!