
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Расчетная формула
|
|
|
|
Потенциальность электростатического поля. Скалярный потенциал. Неоднозначность скалярного потенциала и его нормировка. Потенциал точечного заряда, системы точечных зарядов и непрерывного распределения зарядов.
Потенциал электростатического поля.Способы описания электростатического поля:
1) Векторный (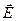 ) – силовая характеристика,
) – силовая характеристика,
2) Скалярный (φ) – энергетическая характеристика.
φ (x,y,z) -- потенциал электростатического поля, скалярная характеристика электростатического поля полностью (!) описывающая электростатическое поле
φ (x,y,z) <=> 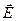 (x,y,z) (т.е зная φ можно восстановить
(x,y,z) (т.е зная φ можно восстановить 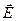 и наоборот). В СИ единица измерения φ = [В]
и наоборот). В СИ единица измерения φ = [В]
Определение Разностью потенциалов в двух точках (1) и (2) φ-φ2 -- называется отношение A12 (работы по перемещению пробного единичного положительного заряда из (1) в (2), которую совершает поле) к заряду qпр.
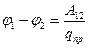
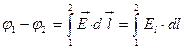
интеграл может быть взят по любому пути соединяющему (1) и (2)
если (1) и (2) лежат на силовой линии, то в качестве линии, соединяющей (1) и (2) нужно взять силовую.
Понятие потенциала можно ввести для любого потенциального векторного поля. (потенциал гравит. силы, потенциал скорости и т.д.)
Потенциал Часто в качестве точки (2) выбирают точку, потенциал которой по определению = 0.
φ2 = 0
В теории – такая точка бесконечно удаленная: 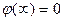 .
.
Замечание Это можно сделать лишь тогда, если заряды располагаются в ограниченной области пространства и их нет на бесконечности.
На практике 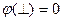 -- потенциал земли = 0.
-- потенциал земли = 0.
Потенциал электростатического поля в т. B(x,y,z) назыв.
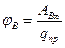 потенциал какой-то точки, когда в ¥ = 0.
потенциал какой-то точки, когда в ¥ = 0.
Расчетная формула: 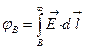
Потенциал поля точечного заряда
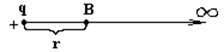 Рис. 18
Рис. 18
|
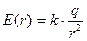
Путь из точки B в ∞ может быть любым, т.к. поле потенциально. Наиболее удобно выбрать L вдоль радиуса вектора, проведенного из точечного заряда
=> dl = dr;
El = Er = E(r); => 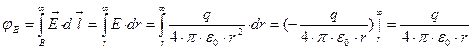 =>
=>
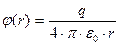 формула имеет смысл для r ≠ 0, т.к. r →∞.
формула имеет смысл для r ≠ 0, т.к. r →∞.
Т.к. поле точечного заряда фундаментально => для нахождения потенциала поля системы зарядов нужно применить принцип суперпозиций:
потенциал поля системы точечных зарядов равен сумме потенциалов, издаваемых в рассматриваемой точке каждым из зарядов.
а) потенциал поля системы точечных зарядов:

б) потенциал поля непрерывного распределения зарядов:

где dq = ρ∙dV -- при объемном распределении заряда,
dq = σ∙dS -- при поверхностном
dq = λ∙dl -- при линейном.
Применение формулы поля точечного заряда и принципа суперпозиций составляет основу метода непосредственного интегрирования и позволяет рассчитать потенциал поля новой системы зарядов. Графически потенциал изображается в виде эквипотенциальных поверхностей и линий на которой он принимает постоянное значение = const.
Примеры расчета потенциала
(I) Равномерно заряженная бесконечная нить. (Рис. 19)
Дано: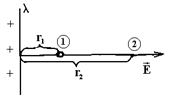 l;
l;
_____________
j (r1)-j(r2) -?

Т.к. поле нити имеет осевую симметрию и 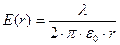 => в качестве линии L, соединяющей 1 и 2 берем отрезок силовой линии, соединяющей точки 1 и 2. =>
=> в качестве линии L, соединяющей 1 и 2 берем отрезок силовой линии, соединяющей точки 1 и 2. => 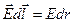 =>
=>
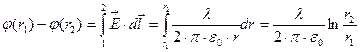
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 418; Нарушение авторских прав?; Мы поможем в написании вашей работы!