Получение ФРС системы методом решения системы логических уравнений

Структурно-сложные системы могут содержать большое количество элементов, обменивающихся различными видами ресурсов: энергией, веществрв и информацией и т.д. Если описать взаимосвязи между элементами с помощью системы логических уравнений (СЛУ), то решив данную систему можно получить ФРС. Большое распространение получил следующий метод записи СЛУ.

Пусть техническая система содержит N элементов. Элементы обмениваются различными ресурсами. Каждый элемент для своей работы может требовать ресурсы от смежных элементов. Уточним следующие два понятия:

• под собственной исправностью элемента будем считать отсутствие поломок внутри рассматриваемого элемента; собсвтенную исправность i-ого элемента будем обозначать как в других ЛВ методах с помощью логической переменной ;
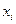• под работоспособностью элемента будет понимать собственную исправность элемента одновременно с работоспособностью смежных элементов-поставщиков необходимых ресурсов для работы рассматриваемого элемента; работоспособность i-ого элемента будем обозначать логической переменной 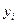; если элемент работоспособен, то он сможет на своем выходе иметь нужный ресурс: электроэнергрию, давление, пар, исполнение заданной функции и т.п.

Исходя из определения, 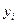является зависимой переменной:

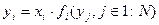
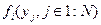- логическая функция, которая отображает зависимость элемента от элементов-поставщиков необходимых ресурсов.

Система логический уравнений, описывающаю функционирование системы с точки зрения исправности элементов будет иметь вид:

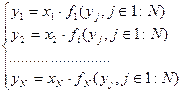
Если решить эту систему относительно 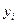, то мы получим фунцию работоспособности для каждого элемента в виде 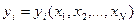. Однако, зачастую этого не требуется. Требуется найти ФР системы на основе некотрого критерия, который можно описать в виде логической функции .

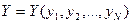В качестве примера рассмотрим систему, заданную следующей структурно-функциональной схемой:

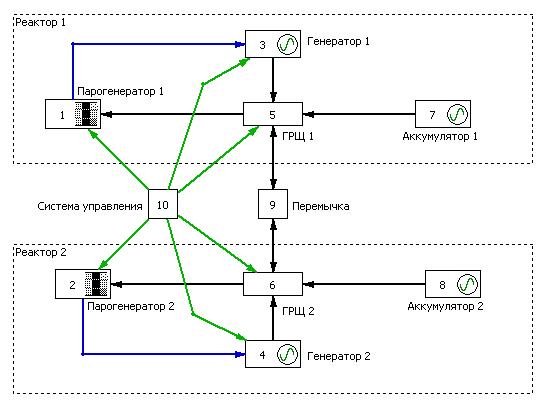
Синим цветом обозначен пар, черным – электроэнергия, а зеленым – управляющие сигналы. СЛ уравнений будет иметь следующий вид:

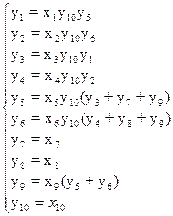
Для пятого элемента (ГРЩ 1) уравнение работоспособности имеет следующий вид:

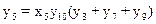
т.е. ГРЩ 1 будет работоспособен, если одновременно:

• не будет отказа оборудования самого ГРЩ 1;
• будет подаваться управление от системы управления;
• будет подаваться энергия от одног из трех альтернативных источников: генератора 1, резервного аккумулятора 1 или от перемычки, связывающей два реактора.

В качестве критерия работоспособности системы можно взять следующие:

• в наличии пар от обоих парогенераторов: ;
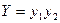• в наличии пар хотя бы от одного из парогенераторов:

В обоих случаях для получения ФРС необходимо решить СЛУ относительно переменных 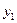и 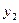, а потом подставить их выражения в формулу для критерия. Тогда мы получим искомую ФРС в виде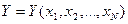

Дата добавления: 2014-01-03