Интегрирование рациональных функций

Рассмотрим интеграл вида , где P(x) и Q(x) – многочлены (такие функции называют рациональными функциями).

Если эта дробь неправильная, то можно выполнить деление с остатком и представить подынтегральную функцию в виде суммы многочлена и правильной дроби.

Например, рассмотрим неправильную дробь

.

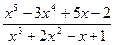Разделим числитель на знаменатель

и выделим целую часть дроби

.

Поэтому в дальнейшем будем рассматривать правильные рациональные дроби.

Из класса всех дробей выделяют основные простые дроби:

где a, p, q, M, N ÎR, k Î N.

Интегралы от первых двух типов простых дробей находятся с помощью подстановки t = x-a:

,

=.

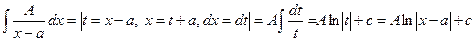Рассмотрим интеграл от третьего типа простых дробей.

· Интеграл вида 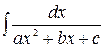находят путем выделения полного квадрата в знаменателе и сведения к табличному интегралу (8) или (10).

(Интеграл вида 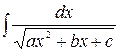находят путем выделения полного квадрата в знаменателе и сведения к табличному интегралу (9) или (11)).

· Интегралы вида (и ) находят путем выделения в числителе производной знаменателя и сведения к интегралам рассмотренных выше видов.

Пример 1.

Пример 2.

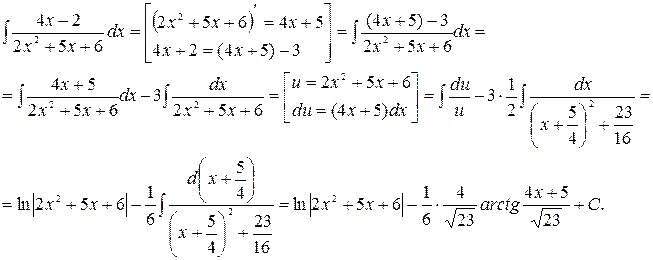
Если подынтегральная функция не соответствует ни одному из перечисленных выше видов, то для взятия интеграла используют тот факт, что любую правильную дробь можно представить в виде суммы простых дробей с помощью следующих теорем.

Теорема 1. Каждый многочлен Q(x) с действительными коэффициентами может быть представлен единственным образом в виде

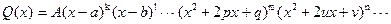, (1) где a, b, …,- корни многочлена кратности k, l, …;

квадратичные множители кратности m, n, … не имеют действительных корней.

Теорема 2. Пусть 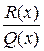- правильная рациональная дробь, у которой знаменатель представлен в виде (1). Тогда эту дробь можно единственным образом представить в виде суммы простых дробей:

, (2)

где - некоторые действительные числа.

Выражение (2) называется разложением рациональной дроби на простые дроби, числа 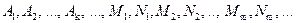- коэффициентами разложения.

Следствие. Пусть 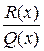- правильная рациональная дробь, у которой знаменатель - многочлен степени n, имеющий n различных действительных корней 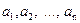. Тогда эту дробь можно единственным образом представить в виде суммы простых дробей:

, (3)

где 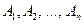- некоторые действительные числа.

Для определения коэффициентов разложения используют метод неопределенных коэффициентов, который состоит в следующем: приводят левую часть равенства (2) или (3) к общему знаменателю и приравнивают коэффициенты при одинаковых степенях многочлена, полученного в числителе и многочлена R(x).

Пример 1. Разложим дробь на простые дроби. Знаменатель имеет два корня - 1 и 2. Воспользуемся формулой (3).

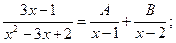
Дата добавления: 2014-01-04