Энтропия. Один из важнейших вопросов для химика, на который термодинамика дает ответ, – возможность и условия протекания химических реакций

Один из важнейших вопросов для химика, на который термодинамика дает ответ, – возможность и условия протекания химических реакций.

Самопроизвольными называют процессы, протекающие самопроизвольно, то есть без привлечения работы извне. А вот в результате осуществления таких процессов как раз и может быть выполнена работа против внешних сил. Примеры самопроизвольных процессов: переход теплоты от горячего тела к холодному, реакция нейтрализации, взрыв смеси водорода с кислородом.

Несамопроизвольными называют процессы, для протекания которых необходима затрата работы извне. Примеры несамопроизвольных процессов: переход теплоты от холодного тела к горячему, распад воды на водород и кислород при комнатной температуре.

Термодинамика оперирует так называемыми равновесными процессами, проходящими через одни и те же состояния, бесконечно близкие к равновесию. Такие процессы являются идеальными, гипотетическими. Реальные, то есть самопроизвольные процессы, в той или иной степени неравновесны.

Под химически обратимыми понимают реакции, которые могут идти в прямом и обратном направлениях. Термодинамически обратимыми называют равновесные процессы, протекающие в прямом, а затем – обратном направлениях так, что не только система, но и окружающая среда возвращаются в исходное состояние. Это без сомнения идеальные (абстрактные) процессы.

Познакомимся еще с одной термодинамической функцией – энтропией S. Ее изменение для обратимого изотермического перехода теплоты от системы к системе составляет:

DS=S₂–S₁=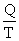 или DS=. (1.13)

Это соотношение фактически выражает второй закон термодинамики.

Для неравновесных (реальных, самопроизвольных) переходов изменение энтропии равно:

DS=(S₂–S₁)>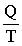. (1.14)

Объединяя эти соотношения, получим:

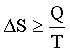. (1.15)

В этом выражении знак равенства относится к обратимым (гипотетическим, нереальным) процессам, а знак неравенства – к реальным (самопроизвольным) процессам.

Энтропия, аналогично энтальпии и внутренней энергии, является однозначной, конечной и непрерывной функцией состояния. Она зависит от природы вещества, агрегатного состояния, температуры, давления. Эта термодинамическая функция чрезвычайно чувствительна к внутреннему устройству системы, степени ее упорядоченности. Наблюдаемое (макроскопическое) состояние системы может существовать при различных распределениях молекул (частиц) по скоростям и координатам, то есть реализуется различными микросостояниями. Число таких микросостояний, которыми реализуется данное макросостояние, называется термодинамической вероятностью W. В отличие от математической вероятности, принимающей значения от нуля до единицы, термодинамическая вероятность – огромное число. Энтропия 1 моль вещества связана с термодинамической вероятностью следующим соотношением:

S=RlnW. (1.16)

По мере понижения температуры число распределений частиц системы по координатам и скоростям уменьшается, то есть уменьшается W. В пределе при 0 К частицы (молекулы) "застынут" и данное макросостояние будет реализовано одним единственным распределением частиц по координатам и скоростям, иными словами термодинамическая вероятность будет равна единице, следовательно согласно соотношению (1.16) энтропия будет равна нулю:

T ® 0 K; W ® 1; S ® 0. (1.17)

Соотношение (1.17) выражает суть третьего закона термодинамики, согласно которому при 0 К энтропия правильно образованного кристалла любого простого вещества или соединения в чистом состоянии равна нулю. Этот закон открывает путь для определения абсолютных величин энтропии. Если вещество находится в стандартном состоянии, то оно характеризуется стандартной энтропией. Величины стандартных энтропии некоторых веществ и ионов при 298,15 К приведены в табл. 1 приложения.

Отметим, что энтропия газа гораздо больше энтропии жидкости, которая в свою очередь больше энтропии кристалла (рис. 2). Это позволяет проводить оценку знака величины DS процесса, которая рассчитывается согласно соотношению:

DS_{реакции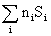} = (продуктов) - 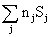(исходных веществ).

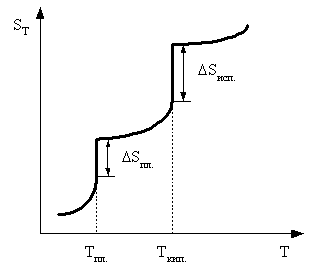
Рис. 2. Температурная зависимость энтропии

Какую же общую полезную информацию дает энтропия для химика?

1. Энтропия характеризует степень упорядоченности в системе, в данном конкретном веществе. Чем ниже S, тем меньше W, тем более компактно вещество, имеет большую твердость, плотность; кристаллические вещества характеризуются меньшей энтропией, чем аморфные вещества, энтропия возрастает с увеличением атомной и молярной масс.

2. Соотношение (1.15) для изолированной системы (Q=0) принимает вид:

DS 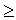0. (1.18)

Соотношение (1.18) означает, что для изолированной системы, в которой протекают обратимые процессы, энтропия постоянна (DS=0) и возрастает (DS>0) в необратимом (реальном, самопроизвольном) процессе. Таким образом, получаем критерий самопроизвольного протекания процессов
в изолированной системе – самопроизвольно идут процессы, приводящие к росту энтропии. Очевидно, самопроизвольное течение процесса будет возможно до тех пор, пока энтропия не достигнет максимального значения. Указанный критерий весьма ограниченный, так как изолированные системы крайне редки. Познакомимся с более общим критерием, и предварительно введем еще одну термодинамическую функцию.

Дата добавления: 2014-01-04