Включение цепи с резистором и конденсатором на синусоидальное напряжение

Включение цепи с резистором и конденсатором на постоянное напряжение (заряд конденсатора)

Из схемы, приведенной на рис. 1.10, следует, что установившаяся составляющая напряжения на конденсаторе u_Cу = U, а свободная составляющая, очевидно, равна

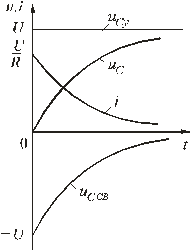
Рис. 1.10

u_Cсв = A e^-t/τ, τ = RC.

Полагаем, что до замыкания ключа конденсатор не был заряжен (Uс(0_-) = 0). На основании законов коммутации u_C(0_-) = u_C(0₊) = 0, при t = 0; следовательно:

u_C(0) = u_Cу(0) + u_Cсв(0) или 0 = U + A, откуда А = -U.

Тогда переходное напряжение на конденсаторе

u_C = U (1 - e^-t/τ),

а переходный ток в цепи

.

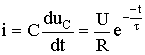Зависимости напряжений и токов от времени показаны на рис. 1.10. Из них видно, что напряжение на конденсаторе возрастает по экспоненциальному закону от нуля до напряжения источника, а ток уменьшается от начального значения до нуля также по экспоненте. Длительность их изменения определяется постоянной времени τ = RC. Здесь как и в п.1.5.1 время переходного процесса принимается равным t ≈ (3 ÷ 5)τ.

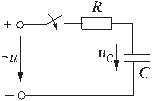
Рис. 1.11

Пусть напряжение источника изменяется по закону

u = U_m sin(ωt + ψ).

Установившаяся составляющая напряжения на конденсаторе (см. рис. 1.11) равна:

u_Cу = -U_m X_C / Z sin(ωt + ψ – φ – π / 2).

где: 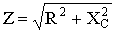- полное сопротивление цепи;
X_C = 1 / (ωC) – емкостное сопротивление;
φ = -arctg(X_C / R) – угол сдвига фаз между установившимся током в цепи и приложенным синусоидальным напряжением.

Свободная составляющая напряжения на конденсаторе

u_Cсв = A e^-t/τ, τ = RC.

Переходное напряжение на конденсаторе

.

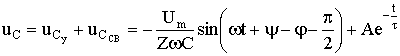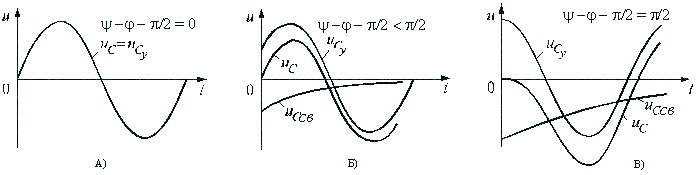
Рис. 1.12

Полагая, что u_C(0_-) = 0, для постоянной интегрирования получим

.

Окончательно напряжение на конденсаторе можно записать в виде

.

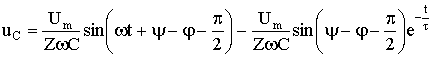Ток в цепи

.

Зависимости переходного напряжения на конденсаторе от времени при различных значениях разностей ψ - φ показаны на рис. 1.12. Их анализ позволяет сделать следующие выводы.

Если в момент включения мгновенное значение установившегося напряжение на конденсаторе равно нулю (ψ – φ – π / 2 = 0), то и свободная составляющая напряжения равна нулю. В цепи сразу устанавливается режим (рис. 1.12 а).

Если в момент включения мгновенное значение установившегося напряжение на конденсаторе имеет наибольшее значение (ψ – φ – π / 2 = π / 2), то переходное напряжение достигает максимального значения приблизительно через половину периода и может приблизиться к удвоенной амплитуде установившегося напряжения, но не превысит его (рис. 1.12 в).

Дата добавления: 2014-01-04