ЛЕКЦИЯ 6. Теорема об изменении кинетической энергии

Теорема об изменении кинетической энергии

Вопросы лекции:

1. Теорема об изменении кинетической энергии системы, твёрдого тела и материальной точки.

2. Понятие о потенциальных силовых полях и консервативных механических системах.

Тарг, 2009; с. 307 – 314, 317 – 322.

1. Теорема об изменении кинетической энергии системы, твёрдого тела и материальной точки.

Рассмотрим механическую систему, движущуюся относительно инерциальной системы координат под действием внешних и внутренних сил.

Запишем дифференциальные уравнения движения системы:

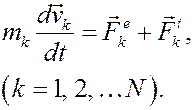
Каждое из уравнений (1) скалярно умножим на вектор скорости соответствующей точки , а затем полученные выражения почленно сложим:

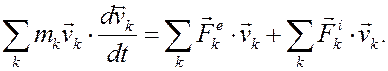
Рассмотрим подробно полученное равенство. Первая сумма в правой части – это сумма мощностей всех внешних сил:

Аналогично, вторая сумма в правой части – это мощность всех внутренних сил системы

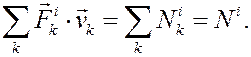
Учитывая, что , каждое слагаемое в сумме левой части может быть преобразовано так

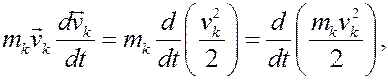
следовательно, считая, что точек в системе конечное число, и вспоминая определение кинетической энергии системы, левую часть равенства запишем в виде

Используя (2), (3) и (4), получим

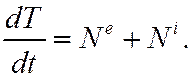
Равенство (5) выражает теорему об изменении кинетической энергии системы в дифференциальной форме:

производная по времени от кинетической энергии системы равна мощности всех внешних и внутренних сил, действующих на систему.

При решении практических задач чаще приходится применять эту теорему в интегральной форме. Получим эту форму теоремы.

Для этого умножим обе части равенства (5) на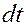

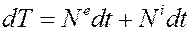
и вычислим интегралы от обеих частей полученного выражения на перемещении из начального положения системы в конечное – :

В левой части полученного равенства получим (интеграл от дифференциала!)

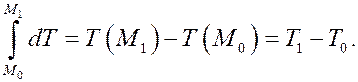
Для первого выражения в правой части получим

аналогично – для второго выражения

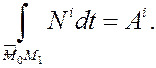
В результате получим равенство

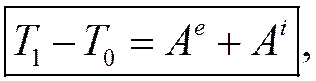
которое и выражает теорему об изменении кинетической энергии системы в интегральной форме:

изменение кинетической энергии системы на произвольном её перемещении равно сумме работ всех внешних и внутренних сил на этом перемещении.

Важное отличие теоремы об изменении кинетической энергии системы в формах (5), или (6), от остальных общих теорем динамики состоит в следующем:

1) теорема носит скалярный характер: все величины, входящие в теорему – скалярные;

2) в теорему входят не только внешние силы, но и внутренние: изменение кинетической энергии системы зависит и от работ, совершенных внутренними силами!!

Теперь получим теоремы об изменении кинетической энергии для твердого тела и для материальной точки.

Как было доказано ранее, в случае твердого тела внутренние силы работы не совершают (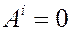; расстояния между любой парой точек тела не изменяются!), поэтому

теорема об изменении кинетической энергии для твердого тела записывается в виде:

в дифференциальной форме, и в виде

в интегральной форме.

Для материальной точки кинетическая энергия всегда вычисляется по одной и той же формуле (формула (1) прошлой лекции)

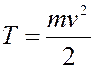
и, кроме того, для точки все силы – внешние. Поэтому можно записать:

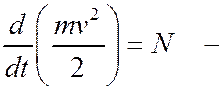
в дифференциальной форме, и

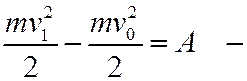
в интегральной форме.

Рассмотрим несколько примеров применения теоремы об изменении кинетической энергии.

Пример 1. Тонкий однородный стержень массы m и длины прикреплен к шарниру с горизонтальной осью вращения и висит неподвижно. В некоторый момент свободный конец стержня толкают горизонтально со скоростью .

Пренебрегая силами трения в шарнире и сопротивления воздуха, найти максимальный угол отклонения стержня от вертикали.

РЕШЕНИЕ. Применим интегральную форму (8) теоремы об изменении кинетической энергии для твёрдого тела

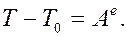
Начальное состояние стержня: стержень висит вертикально и его концу сообщают горизонтальную скорость .

Конечное состояние стержня: он отклонился на максимальный угол и, следовательно, остановился.

В силу этого, учитывая, что стержень совершает вращательное движение:

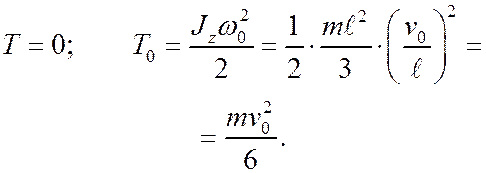
Находим работу внешних сил. На стержень действуют

реакция шарнира О – R и сила тяжести Р. Очевидно, что

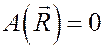
(точка приложения неподвижна). Работу силы тяжести находим по универсальной формуле (21) прошлой лекции

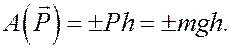
В данном случае центр тяжести стержня при движении поднимается вверх, поэтому в формуле берём знак «–». Находим высоту, на которую поднимется центр тяжести стержня.

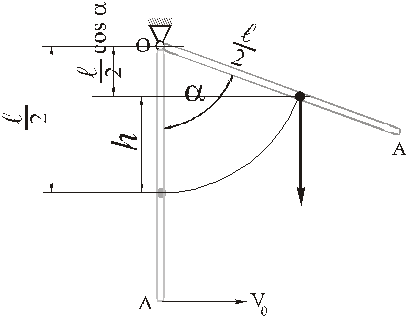
Из рисунка следует

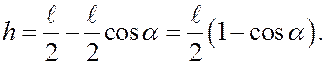
Следовательно,

Подставив выражения для кинетической энергии и работы в теорему, находим

Искомый угол α существует, если

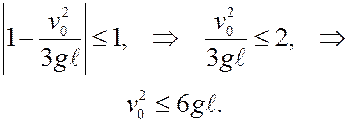
При выполнении этого условия

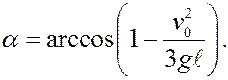
При нарушении условия, т.е. при

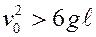
максимального угла не существует, а стержень переходит в режим непрерывного вращения вокруг оси О.

В частности, легко подсчитать:

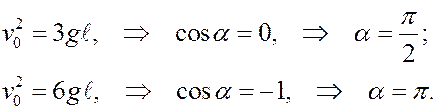
Пример 2. Тело 1 с массой m₁ = 2m установлено на наклонную гладкую плоскость с углом наклона α = 30°. Тело привязано к невесомой нерастяжимой верёвке, переброшенной через блок 3, массой которого можно пренебречь. Второй конец верёвки намотан на однородный цилиндр 2 массы m₂ = m и радиуса R. Цилиндр может катиться по горизонтальной плоскости. Его центр прикреплён к пружине жесткости . В некоторый момент

груз отпускают, и он начинает без начальной скорости скользить вниз по наклонной плоскости.

Пренебрегая массой пружины, считая, что вначале пружина не деформирована, а цилиндр начинает катиться без скольжения, определить скорость тела 1 к тому моменту, когда оно пройдёт путь s. Жесткость пружины принять равной

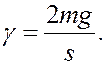
РЕШЕНИЕ. Рассматривается механическая система: тело+цилиндр. Поэтому применяем теорему (6)

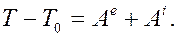
В начальный момент – система находилась в покое. Следовательно,

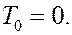
Находим кинетическую энергию системы в конечный момент. Согласно определению

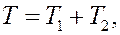
где 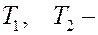кинетические энергии первого и второго тел, соответственно.

Когда тело 1 пройдёт расстояние s его скорость станет равной v. У колеса 2 при этом скорость центра будет равна v₂, а угловая скорость .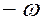

Тело 1 движется поступательно

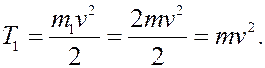
Колесо 2 совершает плоское движение, является сплошным однородным цилиндром и катится без скольжения по неподвижной плоскости. Согласно предыдущей лекции можем сразу записать

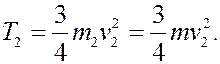
Выразим скорость v₂ через искомую скорость v.

Т.к. верёвка нерастяжима, то скорость верхней точки колеса равна v. Т.к. колесо катится без скольжения, то в точке контакта с дорогой – мгновенный центр скоростей, поэтому

Следовательно,

а кинетическая энергия всей системы будет

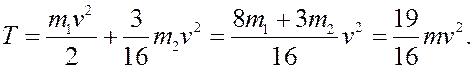
Находим работы сил, действующих на систему. Внутренними силами в системе будут натяжения верёвки.

Т.к. верёвка не растяжима, то (расстояния между любыми двумя точками верёвки постоянны)

Внешними силами будут: силы тяжести, реакции

плоскостей, сила упругости и сила трения между колесом и плоскостью (колесо катится без скольжения).

Очевидно, что

Т.к. в точке контакта с дорогой – мгновенный центр скоростей, то 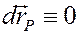и

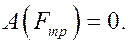
Остаётся найти работы силы тяжести тела 1 и силы упругости пружины. По формуле (21) прошлой лекции (тело опускается вниз)

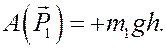
А по формуле (22) той же лекции ()

Находим h и .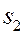

Из рисунка следует

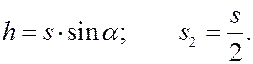
Следовательно,

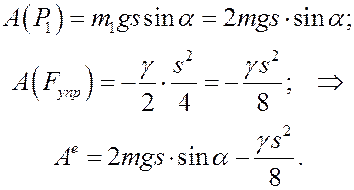
При исходных данных задачи работа будет

Подставив найденные значения в теорему

найдём

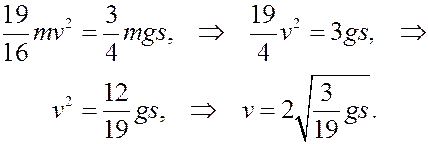
2. Понятие о потенциальных силовых полях и консервативных механических системах.

Силовое поле – это область пространства, в каждой точке которой на помещённую туда частицу действует сила, зависящая от положения частицы.

Примеры: поле силы тяжести, поле силы упругости, гравитационное поле, электрическое поле и т.п.

Если в указанной области пространства ввести какую-либо систему координат Oxyz, то согласно определению

Примеры.

1) Поле силы тяжести (ось z направлена вверх):

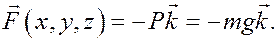
2) Поле силы упругости (ось x – вдоль оси пружины, начало отсчета О – в положении недеформированной пружины):

3) Гравитационное поле (начало отсчета О – в центре притяжения):

Силовые поля могут быть:

а) одномерными; одна компонента силы и зависит от одной координаты; например,

примеры: поле силы тяжести и поле силы упругости;

б) двумерными; две компоненты силы и зависят от двух координат, например

пример: гравитационное поле на плоскости;

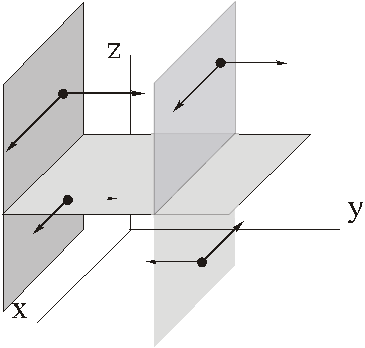
г) трёхмерными; три компоненты силы, зависящие от трёх координат

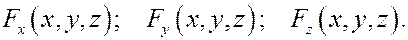
Рассмотрим движение точки в силовом поле. Вычислим элементарную работу этого силового поля:

Все силовые поля делятся на два класса.

Первый: существует такая функция координат

что выражение для элементарной работы

является полным дифференциалом от этой функции, взятым со знаком «–»:

Второй класс полей: такой функции не существует, т.е. выражение

не является полным дифференциалом ни для какой функции.

В первом случае, когда выполнено равенство (11), силовое поле называется потенциальным силовым полем, а функция координат

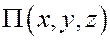
называется потенциальной энергией силового поля.

Второй класс полей, когда функции 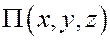не существует, называют непотенциальными силовыми полями.

Потенциальные силовые поля обладают важным преимуществом перед непотенциальными. Действительно, вычислим работу потенциального силового поля на перемещении частицы из положения в положение на каком-либо пути 1.

Имеем, по определению,

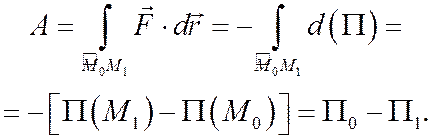
Окончательно получаем

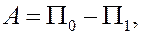
т.е., во-первых, работа потенциального силового поля равна разности значений потенциальной энергии в начальном и конечном положениях частицы и, во-вторых, эта работа не зависит от пути, по которому частица движется из начального положения в конечное:

В случае не потенциальных силовых полей это не так: работа непотенциального силового поля зависит от пути, по которому частица движется из начального положения в конечное

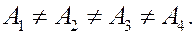
В силу сказанного возникает важный вопрос: как определить, является ли силовое поле потенциальным, или нет?

Из равенства (11) следует, что если оно справедливо для функции 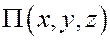, то это равенство будет справедливо и для любой функции, равной

Поэтому потенциальная энергия определена не однозначно, выбором постоянной можно изменять её значения в данной точке пространства. Например, можно считать, что

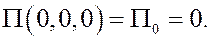
Пусть существует потенциальная энергия 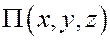. Тогда

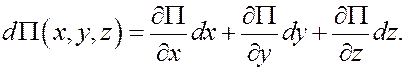
Сравнивая левую и правую части (11)

найдём

Из равенства (14) следует

Из полученных соотношений можем заключить.

Одномерные силовые поля, 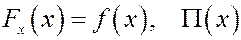, всегда потенциальны:

Дата добавления: 2014-01-04