Примеры. 1) Поле силы тяжести (ось z направлена вверх):

1) Поле силы тяжести (ось z направлена вверх):

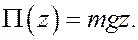
2) поле силы упругости пружины (ось x направлена в сторону растяжения пружины, начало отсчета – в положении недеформированной пружины)

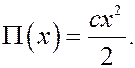
Двумерные и трёхмерные силовые поля могут быть как потенциальными, так и не потенциальными. Условия потенциальности этих полей получаются из условия непрерывности функции 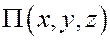вместе со своими производными до второго порядка включительно.

Для двумерных силовых полей условие потенциальности имеет вид

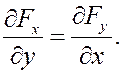
Для трёхмерных:

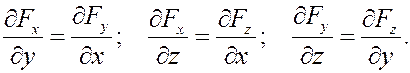
Пример непотенциального двумерного силового поля (соленоидальное поле)

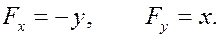
Пусть механическая система движется в потенциальных силовых полях, и пусть 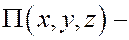суммарная потенциальная энергия. Тогда в теореме (6)

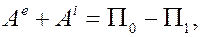
и теорема запишется в виде

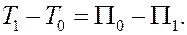
Это равенство можно переписать так

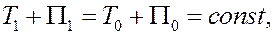
т.е. при движении в потенциальных силовых полях сумма кинетической и потенциальной энергии системы сохраняется.

Сумма кинетической и потенциальной энергии системы называется полной механической энергией системы.

Если полная механическая энергия системы сохраняется, то такая система называется консервативной системой.

Полученное равенство

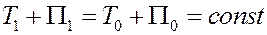
означает, что

Дата добавления: 2014-01-04