Геометрическое определение вероятности

Классическое определение вероятности

Событие называется благоприятствующим событию А, если появление этого события повлечёт появление события А.

Пусть пространство элементарных событий Ω:

1. Состоит из конечного числа элементов

2. Элементарные исходы ω₁, ω₂, … и т.д. равновозможны (т.е. нет оснований считать, что одно происходит чаще другого)

Вероятностью события А называется отношение числа благоприятствующих этому событию исходов к общему числу всех равновозможных исходов:

,

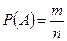где m – число благоприятных исходов, n – общее число исходов.

Свойства, которыми обладает статистическая вероятность, справедливы и для классического определения вероятности.

Минусы: пространство событий должно быть конечномерным, а также очень сложно определить равновозможность исходов.

Если число равновозможных исходов бесконечно и несчетно, то используется геометрическое определение вероятности.

Пусть каждый результат испытаний определяется случайным положением точки в некоторой области Ω (отрезок, фигура на плоскости или тело в пространстве, мера которой будет μ (Ω)). Мера области – длина отрезка, площадь области или объем тела. Наступлению события А благоприятствует попадание точки в область А 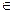Ω.

Тогда геометрическая вероятность будет вычисляться следующим образом:

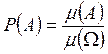
Таким образом, по геометрическому определению, вероятность находится как отношение мер.

Свойства, которыми обладает статистическая вероятность, справедливы и для геометрического определения вероятности.

Пример 2: Два друга договорились встретиться в парке. Встреча должна произойти в течении часа (промежуток времени от 0 до 1). Пришедший первым ждёт второго максимум 15 минут, потом уходит. Какова вероятность встречи двух друзей?

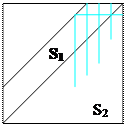
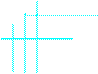
Элементарный исход в том, что один появляется в момент Х, другой – У. Область возможных положений точек х, у будут точки квадрата: 0≤ х ≤ 1; 0 ≤у ≤ 1.

у

y ≤ x + 0,25

y › x -0,25

0 х

Итак, встреча будет, если выполнятся следующие условия:

1.

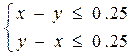
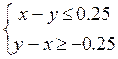
Следовательно,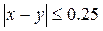

2. x = y – это условие благоприятствует их встрече.

Благоприятное событию А – заштрихованная область

Таким образом, можно подсчитать вероятность наступления события А (встречи друзей) так:

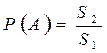
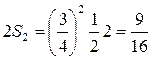
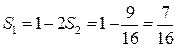
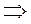
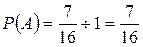
Дата добавления: 2014-01-04