Лекция 2. Аксиоматическое определение вероятности

Аксиоматическое определение вероятности

Существует огромный класс событий, не обладающих симметрией исходных событий, следовательно, по классической схеме их вероятность вычислить нельзя.

Поэтому и используется аксиоматический теоретико-множественный подход.

Рассматривается пространство исходов Ω, в котором исходу из множества (А 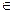Ω), соответствующему некоторому событию А, ставится в соответствие вероятность события Р (А). Это число должно удовлетворять нескольким аксиомам.

Замечание:

Если Ω – пространство элементарных событий, а S – некоторый класс подмножеств множества Ω, то совокупность S называется алгеброй случайных событий, если для неё выполнены условия:

1. ;

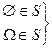2. если события 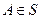и 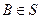, следовательно ;

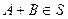3. если события 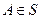и 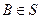, следовательно ;

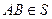4. если события 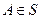следовательно .

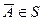Алгебра событий S замкнута относительно операций сложения, умножения.

Если же алгебра замкнута относительно бесконечных пересечений и объединений, то она называется σ-алгеброй событий S (сигма).

Вероятность – вещественная функция Р(А), определённая для каждого события алгебры S и удовлетворяющая следующим аксиомам:

1. Неотрицательность: Р(А)≥0.

2. Нормировка: Р(Ω) = 1.

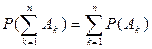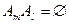3. Аддитивность: вероятность от суммы попарно несовместных событий равна сумме их вероятностей: , где при 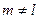(т.е. попарно несовместные).

Замечание: Последнее свойство распространяется на случаи бесконечного числа событий.

В случае если множество Ω содержит n элементов, то число всех подмножеств равно 2ⁿ является алгеброй случайных событий S. Каждый элемент алгебры, т.е. все подмножества из этих 2ⁿ подмножеств есть случайное событие.

Пример 1: Пусть Ω содержит 3 элементарных исхода.

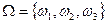_, т.е. n = 3, значит 2ⁿ = 2³=8 – число всех подмножеств множества Ω.

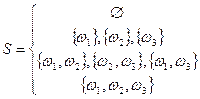
Можно установить взаимнооднозначные соответствия между элементами алгебры S и последовательностями из 0 и 1 по правилу: элемент с номером k из множества Ω включается в подмножество, соответствующее данной последовательности из 0 и 1, если на некотором месте последовательности стоит 1.

Число последовательности из 0 и 1 длины N равно λ^N, т.е.:

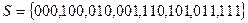
Тройку 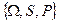, которая вводится при формализации вероятностной задачи, называется вероятностным пространством.

Следствия:

1. Вероятность от невозможного события равняется нулю:

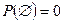
Доказательство: 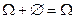и т.к. 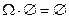(несовместны), то по 3 аксиоме

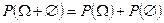
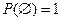Приравняем правые части: 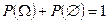, ч.т.д.

2. Вероятность от противоположного события равна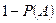

Доказательство: 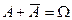– достоверное событие

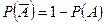
По 3 аксиоме: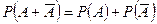

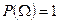(по аксиоме 2)

Приравняем правые части:

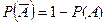, ч.т.д.

3. 0 ≤ Р(А) ≤ 1

Доказательство: 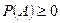– по аксиоме I

Из свойства 2: 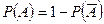, а т.к. вероятность события ≥ 0, то: 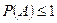, ч.т.д.

4. Если А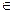В, то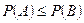

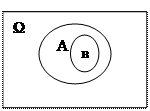
Доказательство:

Запишем событие В, как объединение двух несовместных событий:

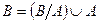, тогда по 3 аксиоме 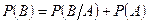, т.к. 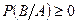, следовательно 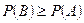, ч.т.д.

5. Обобщённая теорема сложения.

Пусть А и В совместны, т.е. А∩В ≠ Ø

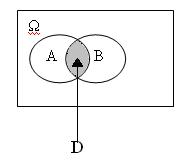
Тогда вероятность от суммы: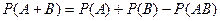

Доказательство:

Сумму (А+В) представим, как объединение несовместных событий: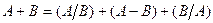

И событие А тоже: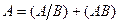

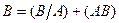
По 3 аксиоме: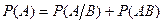

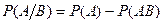
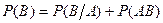
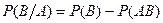
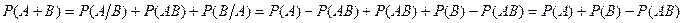
Если 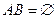(несовместные), то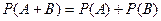

Формула из 5 пункта распространяется на любое конечное число событий.

Докажем, что 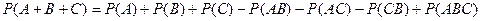, где А, В, С – совместные события.

Доказательство: По обобщённой теории сложения вероятностей и по аксиоме III:

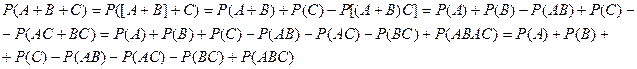ч.т.д.

Пример 2:

1. В колоде 36 карт. Козырь объявлен. Какова вероятность того, что вынутая карта будет козырем или тузом?

Событие А - вынут козырь, событие В – вынут туз. События А и В совместны.

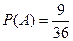
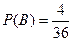
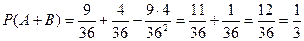
2. В урне 3 шара – 2 белых и один черный. Подряд вынимают 2 шара.

Достают 2 белых шара – событие А, 1 белый и 1 черный – событие B.

Занумеруем все шары:

Белые – 1, 2; черный – 3

При вынимании 2 шаров: 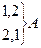по классическому определению: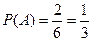

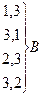по классическому определению: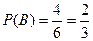

§ Основные соединения в комбинаторике

1. 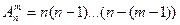число размещений из n по m;

2. 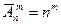число размещений с повторениями из n элементов по m;

3. 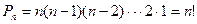число перестановок ;

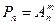4. 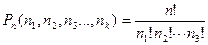число перестановок с повторениями;

5. 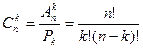число сочетаний элементов из n по k;

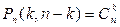, если n₁=k, n₂=n-k

§ Условная вероятность

Вероятность события А, найденная при условии осуществления события В, называется условная вероятность: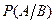

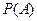, найденная без каких-либо событий – безусловная.

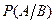характеризует зависимость события А от В.

По классическому определению:

Пусть проведено n испытаний, событию А благоприятствует m испытаний, событию В – k-случаев, следовательно это безусловная вероятность.

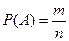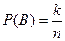, . А благоприятствуют одновременному появлению событий А и В – r случаев: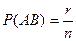

Если событие В произошло, то для события А общее число возможных случаев сокращается до k раз. Из них благоприятствует событию А r-случаев:

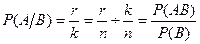
Замечание: при аксиоматическом определении вероятности формула принимается за определение условной вероятности.

§ Теорема умножения вероятности

Вероятность произведения двух любых событий равна произведению одного из них на условную вероятность второго при условии, что первое произошло:

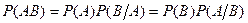
Пример 3: В урне 5 шаров: 3 белых и 2 черных.2 шара вынимают последовательно. Найти вероятность того, что оба шара белых.

Событие А: в первый раз вытащили белый шар.

Событие В: во второй раз вытащили белый шар.

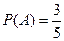
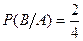
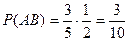
Дата добавления: 2014-01-04