Лекция 6. Частный случай Функции Лапласа

Частный случай Функции Лапласа

Пусть α = - t, a β = t или |α| = |β|

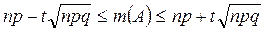Разделим на n:

Вычтем p:

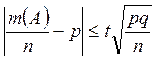И получаем:

(по свойству 1)

§ Случайные величины. Основные понятия и определения

Рассмотрим пространство элементарных событий Ω. В этом пространстве задаётся некоторая область и в ней числовая функция, определённая на этом пространстве, которая в результате испытания примет единственное возможное значение Х(ω_i) – случайная величина. 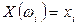, где x_i – число.

А тот факт, что случайная величина примет какое-то конкретное значение будет случайным событием.

Пример 1: Ига в кости: при бросании игрального кубика возможно 6 элементарных исходов: ω₁, ω₂, …,ω₆ . Тогда Х(ω_i) – число очков, выпавших на верхних гранях при бросании кубиков.

Х(ω_i) = i 1 ≤ i ≤ 6

Случайные величины обозначаются х, y, z...а их значения – x_i, y_i, z_i …

Рассматривается пространство элементарных событий Ω: случайной величиной Х называется функция, заданная на пространстве Ω и принимающая определенные вещественные значения:

, ;

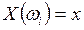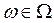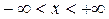
При этом предполагается, что все события вида:

1. , где S – алгебра событий.

Т.е. для всех этих событий определены их вероятности.

Аналогично для событий видов:

2.

3.

Случайная величина характеризуется значениями, которые она принимает и вероятностями, с которыми эти значения появляются. Нельзя заранее предсказать какое из своих возможных значений примет случайная величина, известны лишь вероятности, с которыми эти значения появляются.

В отличие от детерминированного подхода, устанавливающего жёсткую функциональную связь между аргументом и функцией, для случайной величины можно указать, априорно - до опыта - лишь вероятности попадания случайной величины в некоторые случайные числовые множества. Можем посчитать вероятности: 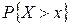, , , где x, a, b – числа.

Различают случайные величины дискретного вида (ДСB) и непрерывного вида (НСB).

ДСB – случайная величина, принимающая отдельные изолированные значения с определённой вероятностью.

НСB – случайная величина, возможное значение которой заполняют некоторый промежуток.

Пример 2: ДСB: количество звонков, поступивших на АТС в течение дня (т.е. 0, 1, 2,…х, где х – конечное или счетное число)

НСВ: время безотказной работы двигателя .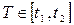

§ Интегральная функция распределения случайной величины

Эта функция является универсальной характеристикой как для ДCB, так и для НСВ.

Функцией распределения случайной величины X (обозначается F(x)) называется вероятность того события, что случайная величина X в результате испытания примет значение меньше, чем х: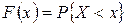

Дата добавления: 2014-01-04