Какой из методов описания термодинамических функций поверхностного слоя показался Вам более оригинальным?

Давайте представим, как с помощью этих двух методов выразить любой термодинамический параметр системы.

По методу Гиббса (участок I на рисунке):

G = G₁ + G₂ + σs,

где G₁ и G₂ – значения энергии Гиббса отдельных фаз в идеализированной системе, соответствующие их объемным значениям, σs – избыток, связанный с разделяющей поверхностью.

По методу слоя конечной толщины (участок II на рисунке):

G = G₁′ + G₂′ + G_сл = G₁′ + G₂′ + G^v_сл + σs,

где G₁′ и G₂′ – энергия Гиббса соответственно фазы 1 и 2 до границы поверхностного слоя (поверхности разрыва).
Применительно к дисперсной системе можно записать объединенное уравнение первого и второго начал термодинамики относительно энергии Гиббса:

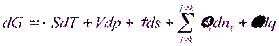
где S – энтропия; dT, dp – изменение температуры и давления; ds – изменение площади поверхности раздела фаз; σ – поверхностное натяжение; μ_i, n_i – химический потенциал и число моль компонента i; φ, q – электрический потенциал и заряд поверхности.

В условиях изобарно-изотермического процесса (dT = 0, dp = 0) в отсутствии физико-химических и электростатических взаимодействий граничных фаз (dn_i = 0, dq = 0) из уравнения получим:

,

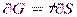Индексы T, p, n_i и q означают, что температура, давление, число моль компонента i и электрический заряд поверхности остаются неизменными.

Таким образом, поверхностное натяжение есть частная производная от энергии Гиббса по площади раздела фаз при постоянной температуре, давлении, в отсутствие химического, электрического и других видов взаимодействия.

Напомним, что кроме энергии Гиббса можно использовать энергию Гельмгольца для описания изменения поверхностной энергии на границе раздела фаз:

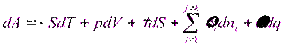
и что существует связь между характеристическими функциями:

dG = dH – TdS

dA = dU – TdS

(Выразите поверхностное натяжение через изменение таких термодинамических функций, как A, H и U.)

Известно, что при повышении температуры поверхностное натяжение чистых жидкостей уменьшается приблизительно по прямолинейному закону, т. е. 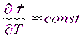и только вблизи критической температуры эта зависимость отклоняется от прямолинейной. (Как Вы объясните, почему с ростом температуры σ уменьшается?)

Отметим, что для индивидуальных веществ, например, для воды без примесей, когда межмолекулярное взаимодействие и формирование поверхностного слоя осуществляется одними и теми же молекулами, значения поверхностного натяжения в энергетическом и силовом выражении (их обозначают единым символом σ) совпадают.

Для растворов, в которых межмолекулярное взаимодействие их компонентов (растворенных веществ и растворителя) различно, значения поверхностного натяжения в виде энергии и силы не совпадают.

, ,

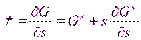для индивидуальных веществ 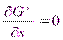, а для растворов .

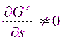Для твердых веществ применение понятий «поверхностное натяжение» и «удельная поверхностная энергия» следует рассматривать с учетом того, что в этом случае работа, затрачиваемая на образование новой поверхности, будет неодинакова в различных местах. Неоднородность поверхности и ограниченная подвижность молекул этих тел будут сказываться на поверхностном натяжении и следует его рассматривать или в определенной точке поверхности или как усредненное значение.

Дата добавления: 2014-01-04