Формула включений и исключений

Основные определения и обозначения

Общие правила комбинаторики

ЭЛЕМЕНТЫ КОМБИНАТОРИКИ

К общим правилам комбинаторики относятся: правило умножения, правило сложения, формула включений и исключений.

Правило умножения. Если объект A можно выбрать m спосабами и если после каждого такого выбора объект B можно выбрать n способами, то выбор пары (A, B) можно осуществить m x n способами.

Правило сложения. Если некоторый объект А можно выбрать m способами, а другой объект В можно выбрать n способами, то выбор “либо А, либо В ” можно осуществить m + n способами.

При использовании правила сложения необходимо следить, чтобы ни один из способов выбора объекта А не совпадал с каким-нибудь способом выбора объекта В. Правила умножения и сложения справедливы для любого конечного числа объектов.

Пусть имеется N предметов, некоторые из которых обладают свойствами . При этом каждый предмет может либо не обладать ни одним из этих свойств, либо обладать одним или несколькими свойствами. Обозначим через 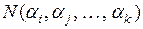число предметов, обладающих свойствами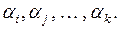

Если предмет не обладает каким-либо свойством, то это свойство пишем с чертой. Например, 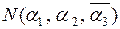- число предметов, обладающих свойствами 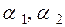и не обладающих свойствами . Число предметов, не обладающих ни одним из указанных свойств, обозначается по этому правилу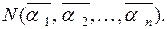

Формула включений и исключений состоит в том, что

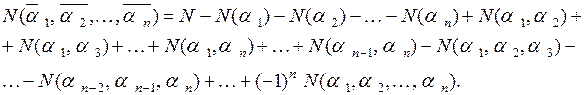Здесь алгебраическая сумма распространена на все комбинации свойств 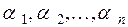(без учета их порядка), причем знак + ставится, если число учитываемых свойств четно, и знак - если это число нечетно.

Дата добавления: 2014-01-04