Общие указания к решению задач

Правила умножения и сложения можно использовать при решении задач самых различных типов. Формулу включений и исключений используют при подсчете числа объектов, обладающих или не обладающих определенными свойствами.

Пример 2. Из пункта А в пункт В можно добраться пароходом, поездом, автобусом, самолетом; из пункта В в пункт С – пароходом и автобусом. Сколькими способами можно добраться из пункта А в пункт С (рис. 6)?

Рис. 6. Варианты добраться до пункта С.

В задаче рассматриваются объекты: 1 – вид транспорта из пункта А в пункт В;

2 – вид транспорта из пункта В в пункт С.

Нужно найти число способов выбора 1 и 2 объектов. Объект 1 можно выбрать четырьмя способами, объект 2 – двумя способами.

По правилу умножения объекты 1 и 2 можно выбрать способами.

Пример 3. Сколько существует четырехзначных двоичных чисел?

Если допустить, что числа могут начинаться с нуля, то когда каждую цифру числа можно выбрать двумя способами (в двоичной системе используются две цифры 0, 1). По правилу умножения получаем, что четырехзначных двоичных чисел будет .

Пример 4. Сколько четырехзначных чисел можно составить из цифр 0, 1, 2, 3, 4, 5, если:

а) ни одна из цифр не повторяется более одного раза;

б) цифры могут повторяться?

Решение:

а) первую цифру можно выбрать пятью способами, это может быть любая цифра из цифр 1, 2, 3, 4, 5 (нуль не может быть первой цифрой потому, что в таком случае число не четырехзначное), вторую цифру можно выбрать пятью способами. Так как цифры не должны повторяться, то третью цифру можно выбрать четырьмя способами, четвертую цифру - тремя способами.

Согласно правилу умножения общее число способов равно

б) первую цифру можно выбрать пятью способами, а каждую следующую цифру шестью способами, так как цифры могут повторяться. Таким образом, число искомых чисел равно

Пример 5. В научно-исследовательском институте работает 67 человек. Из них 47 знают английский язык, 35 – немецкий и 23 – оба языка. Сколько человек в институте не знают ни английского, ни немецкого языков?

Решение. Коллектив сотрудников можно разбить на части:

первую из них составляют те, кто знает только английский язык;

вторую – те, кто знает только немецкий язык;

третью – те, кто знает оба языка;

четвертую – те, кто не знает ни одного, ни другого языка.

Применим формулу включений и исключений, для этого введем обозначения:

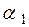– знание английского языка;

– знание немецкого языка;

N – число сотрудников института;

– число сотрудников, знающих английский язык;

– число сотрудников, знающих немецкий язык;

– число сотрудников, знающих оба языка;

– число сотрудников, не знающих ни одного языка.

По формуле включений и исключений получаем:

Пример 6. Пассажир оставил вещи в автоматической камере хранения, а когда пришел получать вещи, выяснилось, что он забыл номер. Он только помнит, что номер содержал числа 23 и 37. Чтобы открыть камеру, нужно правильно набрать пятизначный номер. Какое наибольшее количество номеров нужно перебрать, чтобы открыть камеру?

В данном случае возможны следующие взаимоисключающие комбинации из цифр:

? 2 3 3 7? 3 7 2 3

2 3? 3 7 3 7? 2 3

2 3 3 7? 3 7 2 3?

Знак? стоит на месте забытой цифры.

Этой цифрой может быть любая из десяти цифр 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Таким образом, каждой из 6 комбинаций соответствует 10 различных чисел. По правилу суммы получаем, что общее количество различных чисел равно .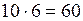

Дата добавления: 2014-01-04