Динаміка обертального руху

Момент сили відносно точки. Моментом сили 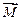відносно точки (центра обертання) є векторний добуток радіуса-вектора 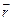, проведеного з центра обертання в точку прикладання сили і самої сили (рис.1. 11):

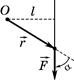
Рис.1. 11

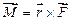. (1.51)

Модуль моменту сили

,

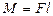де 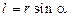– плече сили.

Момент сили відносно осі. Момент сили M_z відносно осі z – це скалярна величина, яка дорівнює проекції на дану вісь вектора моменту сили відносно будь-якої точки цієї ж осі:

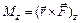, (1.52)

де 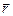– радіус-вектор з точки на осі z у точку прикладання сили .

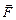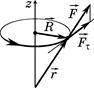
Рис.1. 12

Можна переписати формулу (1.53) у вигляді

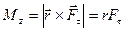, (1.53)

де 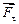– тангенціальна складова сили , тобто складова вздовж дотичної, 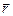– радіус-вектор у площині обертання (рис.1. 12).

Момент інерції тіла. Моментом інерції матеріальної точки називається добуток її маси m на квадрат відстані r від осі обертання:

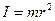. (1.54)

Щоб визначити момент інерції твердого тіла, його потрібно уявно розбити на елементарні маси Dm_i, кожна з яких настільки мала, що її можна уявляти матеріальною точкою, за формулою (1.55) визначити момент інерції кожної елементарної маси, а потім підсумувати по всіх елементарних масах. У результаті отримаємо

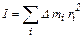. (1.55)

Знак рівності можна поставити тільки під знаком границі при 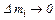, тобто

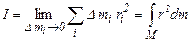. (1.56)

Інтегрування в формулі (1.56) проводиться по повній масі тіла М. Увівши локальну густину

,

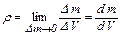отримаємо 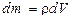, де 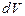– елементарний об’єм.

Тоді формула (1.46) перепишеться у вигляді

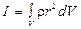, (1.57)

де інтегрування проводиться по об’єму тіла. Якщо тіло однорідне, тобто 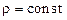, тоді

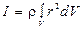. (1.59)

Момент інерції тіла є мірою інертності тіла при обертальному русі, тоді як маса тіла – міра його інертності при поступальному русі.

Для однорідного циліндра маси m і радіуса R при обертанні навколо осі циліндра

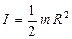. (1.60)

Для однорідної кулі маси m і радіуса R при обертанні навколо осі, що проходить через його центр:

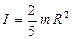. (1.61)

Для однорідного стержня масою m й довжиною l при обертанні навколо осі, що проходить через його центр, і площина обертання перпендикулярна до осі обертання

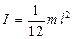. (1.62)

Теорема Штейнера. Момент інерції тіла маси m відносно будь-якої осі дорівнює:

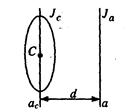
Рис.1.13

I_a = I_c+md² (1.63)

де I_a - момент інерції тіла відносно довільної осі а, I_c – момент інерції тіла відносно осі, яка проходить через центр інерції тіла і паралельна даній, d – відстань між осями.

Момент імпульсу матеріальної точки визначається аналогічно до мо-менту сили. Відносно центра обертання О момент імпульсу (рис.1. 14)

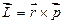, (1.64)

де 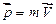– імпульс матеріальної точки, 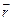– радіус-вектор, проведений з центру обертання О у матеріальну точку.

Модуль моменту імпульсу відносно точки О

L = pl, (1.65)

де 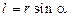– плече імпульсу. Відносно осі обертання z момент імпульсу

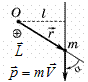
Рис.1. 14

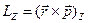, (1.66)

де 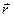– радіус- вектор, проведений з будь-якої точки на осі в матеріальну точку, індекс z у векторного добутку вказує на те, що потрібно взяти проекцію на вісь z.

Момент імпульсу відносно осі можна представити так:

L_z = p_t R, (1.67)

де p_t – тангенціальна складова імпульсу (вздовж дотичної до кола обертання матеріальної точки), R – радіус кола в площині обертання.

Момент імпульсу системи матеріальних точок

. (1.68)

Закон збереження моменту імпульсу. Для окремої матеріальної точки

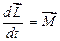, (1.69)

де 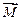– результуючий момент сил, які діють на матеріальну точку.

Для системи матеріальних точок

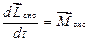, (1.70)

де 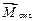– результуючий момент зовнішніх сил, які діють на систему матеріальних точок.

Якщо система замкнена (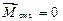), то

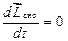і 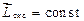. (1.71)

У замкненій системі тіл повний момент імпульсу системи є незмінною величиною.

Момент імпульсу твердого тіла. При обертанні твердого тіла навколо осі симетрії його момент імпульсу прямо пропорційний кутовій швидкості:

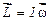, (1.72)

де I – момент інерції тіла, відносно тієї ж осі, 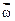– кутова швидкість. Продиференціюємо формулу (1.72) за часом і врахуємо (1.60). У результаті отримаємо:

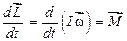. (1.73)

Якщ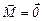о , то . Таким чином, якщо результуючий момент зовнішніх сил, що діють на тіло, M = 0, то добуток 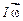залишається незмінним і зміна моменту інерції викликає за собою відповідну зміну кутової швидкості.

Дата добавления: 2014-01-04