Електричне поле в діелектриках

.

У проекціях формула (3.10) запишеться у вигляді

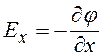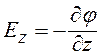; ; . (3.11)

Можна розв’язати і обернену задачу – за відомою напруженістю 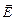визначити різницю потенціалів

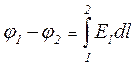, (3.12)

де E_l – проекція вектора 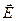на напрям ділянки інтегрування 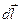, тобто на напрям дотичної в кожній точці контуру інтегрування від точки 1 до точки 2. Інтеграл (3.12) можна брати по будь-якій кривій, що з’єднує точки 1 і 2.

Інтеграл у правій частині (3.12) по замкненому контуру L називається циркуляцією вектора напруженості. З формули (3.12) випливає:

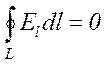. (3.13)

Тобто циркуляція вектора напруженості електростатичного поля дорівнює нулю. Формула (3.13) є однією з чотирьох формул, які вичерпно описують всі властивості електромагнітного поля.

Якщо в будь-якій точці поля вектор 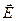незмінний за величиною й напрямком (тобто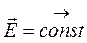), то таке поле називається однорідним. Для однорідного електричного поля

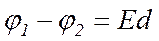, (3.14)

де d – відстань між токами 1 і 2, яку вимірюють уздовж лінії напруженості.

Еквіпотенціальні поверхні – це поверхні, які проведені в електричному полі через точки з однаковим потенціалом. В кожній точці еквіпотенціальної поверхні вектор 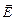направлений вздовж нормалі до неї у бік зменшення потенціалу.

Потік вектора напруженості. Величина

, (3.15)

де – проекція вектора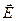на напрям нормалі в кожній точці поверхні інтегрування S називається потоком вектора напруженості через поверхню S (див. рис. 28). Фізичний зміст потоку вектора напруженості полягає в тому, що він визначає кількість ліній напруженості, що перетинають поверхню інтегрування S. Для замкнених поверхонь інтегрування у якості позитивної нормалі береться зовнішня нормаль.

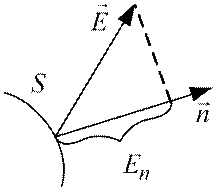
Рис. 28

Теорема Гаусса. Потік вектора напруженості через замкнену поверхню дорівнює сумі зарядів, які знаходяться всередині цієї поверхні, поділеної на електричну сталу e₀ :

. (3.16)

Використовуючи теорему Гауса, легко визначити:

1. Поле нескінченної однорідно зарядженої площини (див. рис. 29, а, б)

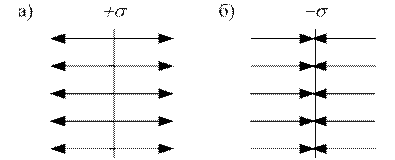
Рис. 29

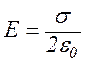, (3.17)

де s – поверхнева густина заряду, тобто заряд, що припадає на одинцю площі поверхні: s=q/S (Кл/м).

2. Поле двох різнойменно заряджених поверхонь (див. рис. 30)

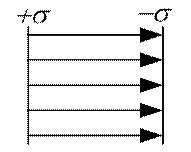
Рис. 30

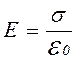. (3.18)

Електричне поле повністю зосереджене між різнойменно зарядженими поверхнями з однаковими густинами заряду і є однорідним.

3. Поле нескінченної, зарядженої циліндричної поверхні:

E (r) =0 (r < R),

(r ³ R),(3.19)

де R – радіус циліндра l – лінійна густина заряду, тобто заряд, який припадає на одиницю довжини, r – відстань від осі до точки спостереження (див. рис. 31). Таким чином, заряджена циліндрична поверхня утворює електричне поле тільки зовні циліндра, всередині циліндра електричне поле відсутнє.

4. Поле двох коаксіальних циліндричних різнойменно заряджених поверхонь.

E (r) =0 (r<R₁),

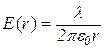(R₁ £ r £ R₂), (3.20)

E (r) =0 (r>R₂),

Рис. 31

Рис. 32

де R₁ – радіус внутрішнього циліндра, R₂ – радіус зовнішнього циліндра (див. рис. 32). Коаксіальними циліндрами називають циліндри зі спільною віссю. Таким чином електричне поле двох коаксіальних різнойменно заряджених циліндрів з однаковою за модулем лінійною густиною заряду повністю сконцентроване між циліндричними поверхнями.

5. Поле зарядженої сферичної поверхні (див. рис. 33)

E (r) =0 (r<R),

(r>R),

Рис. 33

де R – радіус сфери, r – відстань від центра сфери до точки спостереження, q – заряд сфери. Таким чином, електричне поле зарядженої сфери утворюється тільки зовні сфери, всередині зарядженої сфери електричне поле відсутнє.

6. Поле двох концентричних різнойменно заряджених сферичних поверхонь (див. рис. 34):

E (r) =0 (r<R₁),

(R₁ £ r £ R₂), (3.21)

E (r) =0 (r>R₂),

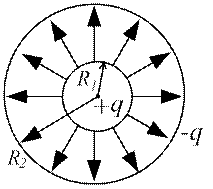
Рис. 34

де R₁ i R₂ – радіуси внутрішньої і зовнішньої сфер. Концентричними називаються сфери зі спільним центром. Таким чином, електричне поле двох різнойменно заряджених концентричних сферичних поверхонь повністю зосереджене між сферами.

Діелектриками називаються речовини, які нездатні проводити електричний струм через відсутність в них вільних електричних зарядів.

Полярні й неполярні діелектрики. Можна ввести радіуси-вектори центрів ваги позитивних і негативних зарядів молекули (див. рис. 35).

Рис. 35

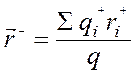; , (3.22)

де – радіус-вектори усередненого за часом положення і -го заряду молекули. Тоді можна вважати, що весь позитивний заряд молекули зосереджений у центрі ваги позитивних зарядів, а негативний – у центрі ваги негативних. У результаті отримаємо так звану дипольну модель молекули. Якщо за відсутності зовнішнього електричного поля:

1) , тобто центри ваги позитивних і негативних зарядів молекули збігаються, то такі молекули називаються неполярними, а діелектрики, утворені з цих молекул, – неполярними діелектриками;

2) 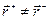, тобто центри ваги позитивних і негативних зарядів молекули не збігаються, то такі молекули називаються полярними, а діелектрики, утворені з цих молекул, – полярними діелектриками.

Для полярних молекул вводиться дипольний електричний момент молекули

, (3.23)

де q – заряд молекули, 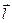– радіус – вектор, проведений із центра ваги негативних зарядів у центр ваги позитивних зарядів молекули.

Молекула в зовнішньому електричному полі. При внесенні в зовнішнє електричне поле з напруженістю :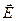

а) неполярна молекула розтягується під дією сил поля і набуває дипольного електричного моменту, який направлений уздовж зовнішнього поля і пропорційний напруженості поля:

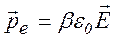, (3.24)

де b – поляризованість молекули (тобто неполярна молекула поводить себе як пружний диполь);

б) полярні молекули розвертаються і встановлюються своїм дипольним моментом 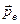за напрямком вектора напруженості зовнішнього електричного поля 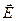(тобто полярна молекула поводить себе як жорсткий диполь).

Поляризація діелектрика. За відсутності зовнішнього електричного поля сумарний дипольний момент діелектрика дорівнює нулю (для неполярного діелектрика дипольнімоменти молекул дорівнюють нулю, для полярного – через повний хаос напрямків дипольних електричних моментів молекул).

Під дією зовнішнього електричного поля діелектрик поляризується – результуючий дипольний момент діелектрика стає відмінним від нуля: неполярні молекули розтягуються і орієнтуються дипольними моментами вздовж зовнішнього електричного поля з напруженістю (див. рис. 36). Ступінь поляризації діелектрика характеризується поляризованістю – дипольним електричним моментом у одиничному об’ємі діелектрика:

; (3.25)

де 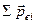– сума дипольних електричних моментів в об’ємі V.

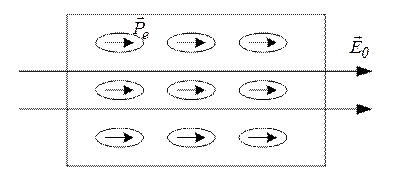
Рис. 36

Для ізотропних діелектриків

, (3.26)

де d – діелектрична сприйнятливість, 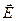– напруженість поля в діелектрику.

Зв’язані заряди. На поверхню діелектрика внаслідок поляризації виступають зв’язані заряди. Там, де лінії напруженості виходять з діелектрика, виступають позитивні заряди, а там, де входять, – негативні (див. рис. 37). Поверхнева густина зв’язаних зарядів визначається за формулою

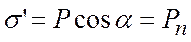, (3.28)

де P_n – проекція вектора поляризованості на зовнішню нормаль до поверхні діелектрика. З урахуванням (3.26) формула (3.27) набуває вигляду

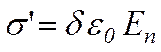, (3.28)

де – проекція напруженості поля всередині діелектрика у безпосередній близькості до поверхні на зовнішню нормаль до поверхні. Формула (3.28) визначає не тільки величину σ, а також її знак.

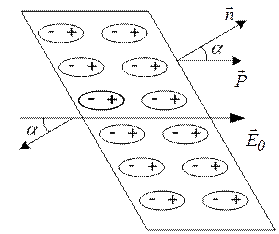
Рис. 37

Опис поля в діелектрику. Внаслідок принцип суперпозиції напруженість електричного поля всередині діелектрика складається з двох компонентів:

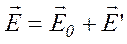, (3.29)

де – напруженість зовнішнього поля, 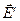– напруженість поля, утвореного зв’язаними зарядами, що виступили на поверхню діелектрика при його поляризації. Вектор 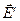завжди направлений протилежно вектору , тому в скалярному вигляді:

, (3.30)

тобто діелектрики завжди послаблюють електричне поле. Поляризація діелектрика обумовлена дією сумарного поля (3.29).

Для опису електричного поля в діелектрику крім вектора напруженості 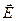вводиться ще вектор електричного зміщення

. (3.31)

У вакуум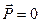і: і .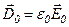

У діелектрику і

,

де e=1+d – відносна діелектрична проникність. Через напруженості полів зовнішнього 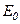і внутрішнього 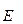відносна діелектрична проникність ε визначається за формулою

. (3.32)

Оскільки за модулем напруженість електричного поля в середині діелектрика завжди менша, ніж напруженість зовнішнього поля у вакуумі, то ε > 1. Відносна діелектрична проникність показує, у скільки разів напруженість електричного поля всередині діелектрика відрізняється від напруженості зовнішнього поля.

Дата добавления: 2014-01-04