Провідники в зовнішньому електричному полі

Умови рівноваги зарядів на провіднику. Рівновага зарядів на провіднику спостерігається при виконанні двох умов:

E=0 – всередині провідника. (3.33)

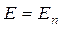– на поверхні провідника. (3.34)

Тобто, всередині провідника поле повинно бути відсутнє, а на поверхні направлене вздовж нормалі до поверхні.

Розподіл зарядів по провіднику. Якщо провіднику надати заряд, то він розподілиться на ньому так, щоб виконувалися дві вище наведені умови рівноваги заряду на провіднику.

Рис. 38

При рівновазі зарядів ні в якому місці всередині провідника не може бути надлишкових зарядів. Всі вони розташуються по зовнішній поверхні провідника (див. рис. 38).

Густина заряду на поверхні провідника визначається кривизною поверхні r=1/R, де R – радіус кривизни. Густина заряду зростає зі збільшенням позитивної кривизни поверхні (опуклості) і зменшується при збільшенні негативної кривизни (вгнутості).

Провідник у зовнішньому електричному полі. При внесенні незарядженого провідника в електричне поле носії заряду у провіднику приходять в рух. На кінцях провідника накопичуються заряди протилежних знаків, які називаються індукційними зарядами (див. рис. 39). Перерозподіл зарядів закінчується тоді, коли будуть виконані обидві умови рівноваги заряду на провіднику.

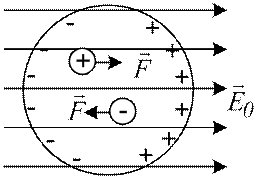
Рис. 39

Індукційні заряди розподіляються по зовнішній поверхні провідника, а поле всередині провідника дорівнює нулю, тому що поле індукційних зарядів компенсує всередині провідника зовнішнє поле. На цьому базується електростатичний захист, тобто захист певних місць простору від електричних полів.

Електроємність провідника. Величина, що характеризується здатністю провідника накопичувати електричні заряди, називається електроємністю:

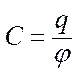, (3.35)

де q – заряд на провіднику, φ – потенціал провідника, тобто потенціал електричного поля в точці на поверхні провідника. З умови рівноваги зарядів на провіднику випливає, що потенціали всіх точок на поверхні провідника однакові, тому говорять про потенціалі всього провідника.

При одному й тому ж потенціалі провідника чим більше його електроємність, тим більший заряд накопичений на провіднику. Електроємність провідника залежить від форми, розмірів провідника і електричних властивостей середовища, що оточує провідник (відносної діелектричної проникності). Для сферичного провідника

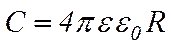, (3.36)

де R – радіус сфери, ε – відносна діелектрична проникність середовища.

Конденсатори. Усамітнені провідники мають малу електроємність. Навіть куля розмірів землі має електроємність близько 700 мкФ. Для накопичення зарядів служать конденсатори – пристрої, які при невеликому потенціалі накопичують значні за величиною заряди. Будова конденсатора базується на тому, що електроємність провідника зростає при наближенні до нього інших тіл. Провідники, що утворюють конденсатор (обкладки), повинні мати таку форму, щоб електричне поле було зосереджене між ними. Тоді наближення зовнішніх тіл не впливає на електроємність конденсатора. Можливі тільки три таких форми обкладинок і три типи конденсаторів: плоско паралельні, циліндричні й сферичні.

Електроємність конденсатора визначається за формулою:

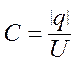, (3.37)

де q – заряд однієї з обкладок, U – різниця потенціалів між обкладками. Для плоского конденсатора

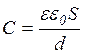, (3.38)

де S – площа обкладки, d – відстань між обкладками, ε – відносна діелектрична проникність середовища між обкладками.

Дата добавления: 2014-01-04