Гіпотеза де-Бройля

КВАНТОВА МЕХАНІКА

Хвильові властивості речовини. В 1924 р. де-Бройль висунув гіпотезу, що двоякість (дуалізм) не є особливістю тільки світла, але має універсальне значення. Він припустив, що частинки речовини поряд з корпускулярними властивостями мають також і хвильові і переніс на випадок частинок речовини ті ж правила переходу від корпускулярної картини до хвильової, які справедливі для світла. Ці твердження отримали назву гіпотези де-Бройля. Фотон має енергію і імпульс

e=հn, p=հ/l.

Енергія і імпульс відбивають його корпускулярні властивості, а частотаn і довжина l – хвильові властивості.

За ідеєю де-Бройля рух будь-якої частинки пов’язаний з поширенням хвилі, довжина якої

l=հ/р (8.1)

а частота – n=e/հ.

Ці хвилі спочатку називали хвилями де-Бройля, а потім вони отримали назву хвилі матерії. Гіпотезу де-Бройля невдовзі було блискуче підтверджено експериментально у досліді з проходження електронного пучка через металеву фольгу (див. рис. 88, а).

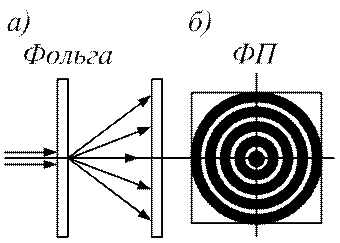
Рис. 88

Прискорений пучок електронів проходить через тонку металеву фольгу і потрапляє на фотопластину (ФП). Електрон при співударі з фотопластиною чинить на неї таку ж дію, як фотон, тобто засвітлює місце попадання. Пучок електронів розсіюється металевою фольгою і дає дифракційну картину, аналогічну до тієї, що має місце при падінні на фольгу рентгенівського

випромінювання (див. рис. 88, б). При цьому дифракційна картина відповідає довжині хвилі

l=հ / mv,

де v – швидкість електронів, тобто збігається з довжиною хвилі де-Бройля з формули (8.1).

Таким чином, матерія двояка, тобто частинки речовини одночасно мають і корпускулярні і хвильові властивості. Це положення називається принципом двоякості.

§2. Квантово-механічний опис руху мікрочастинок

Виникла потреба побудувати механіку, яка б враховувала хвильові властивості частинок. Ця механіка спочатку отримала назву хвильової, а потім квантової механіки.

Рівняння Шредінгера. Основним рівнянням квантової механіки є рівняння Шредінгера. Для стаціонарних станів тобто станів, що не змінюються у часі, рівняння Шредінгера має вигляд

,

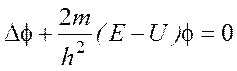де Δ=д²/дx²+д²/дy²+д²/дz² – оператор Лапласа (лапласіан);

m – маса частинки;

U –потенціальна енергія частинки у силовому полі, в якому вона рухається;

E – повна енергія частинки;

f (x,y,z) – хвильова функція.

Хвильова функція. У квантовій механіці стан частинки описується хвильовою функцією f (x,y,z). Фізичний зміст хвильової функції полягає в тому, що квадрат її модуля визначає густину ймовірності знаходження частинки у відповідному місці простору. Тоді імовірність dP того, що частинка буде знайдена у межах об’єму dV визначається формулою

dP=|f|²dV.

Співвідношення невизначеностей. Квантова механіка має статистичний характер. Вона не дозволяє визначити місцезнаходження частинки у просторі або траєкторією, по якій рухається частинка. У застосуванні до мікрочастинок поняття певного місцеположення і траєкторії взагалі відсутні, оскільки рух по певній траєкторії не сумісний з хвильовими властивостями частинок.

Ступінь точності, з якою до частинки можна застосувати уявлення про певне положення її у просторі, дається співвідношенням невизначеностей. Згідно з цим співвідношенням частинка не може одночасно мати точне значення координати і відповідне цій координаті значення імпульсу. Математичне формулювання цього принципу має вигляд

Δx·Δp_x ≥ ħ,

де Δx – невизначеність (абсолютна похибка) координати; Δp_x – невизначеність імпульсу вздовж цієї координати.

Із співвідношення невизначеностей випливає, що чим точніше визначена одна з величин (координата або імпульс уздовж цієї координати), тим більшою стає невизначеність (похибка) іншої величини.

Квантування. Відповідно до свого фізичного змісту хвильова функція f (x,y,z) повинна бути однозначною, кінцевою і безперервною у всій області визначення x,y,z. Рівняння Шредінгера має рішення, яке задовольняє цим умовам, не при будь-яких значеннях енергії Е, а лише при певних визначених значеннях. Отже, енергія частинки у заданому силовому полі квантована, тобто змінюється не безперервно, а дискретно квантами (порціями) енергії з певним для даного силового поля (яке описується потенціальною енергією U) законом квантування. Крім енергії частинки, виявляються квантованими і інші її характеристики (момент імпульсу, тощо).

§3. Атом водню

Енергія атома. В атомі водню потенціальна енергія

U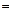–Ze²/r,

де е – заряд електрона, r – відстань електрона від ядра, Z – ціле число.

Якщо Z=1 – це атом водню, а при Z ≠ 1 – воднеподібний атом, тобто атом будь-якого елемента в якого відщеплені всі електрони, крім одного.

Рівняння Шредінгера для стаціонарних станів воднеподібного атому

Δf+2m(E+Ze²/r)f/ħ²=0

має розв’язок в наступних випадках:

1) При будь-яких позитивних значеннях енергії електрона Е. Цей випадок відповідає електрону, що пролітає поблизу ядра і йде знову на нескінченність (див. рис. 89).

Рис. 89

2) При дискретних від’ємних значеннях. Цей випадок відповідає електрону, що знаходиться у межах атому. Енергія електрона при цьому визначається формулою

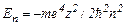(n=1,2,3…).

Квантові числа. Хвильові функції f_n,l,m, що відповідають значенням енергії Е_n, містять три цілочисельні параметри:

1) n – головне квантове число, яке приймає цілочисельні значення n=1, 2, 3…;

2) l – азимутальне квантове число, яке при заданому головному числі n приймає цілочисельні значення l=0,1,2,3,..,n–1 – всього n значень;

3) m – магнітне квантове число, яке при заданому азимутальному числі l приймає цілочисельні значення m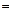–l,…,0,…+l. – всього 2l+1 значень.

Таким чином, кожному значенню енергії Е_n відповідає кілька хвильових функцій f_n,l,m, що відрізняються квантовими числами l і m. Стани з однаковою енергією називаються виродженими. Кратність виродження дорівнює

.

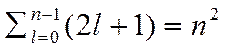Азимутальне квантове число l визначає орбітальний, тобто пов’язаний з рухом по орбіті навколо ядра, момент імпульсу електрона в атомі. Закон квантування моменту імпульсу електрона .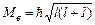

Магнітне квантове число m визначає проекцію орбітального моменту імпульсу на вектор 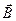магнітного поля. Закон квантування .

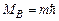Таким чином, орбітальний момент імпульсу електрона в атомі і його проекція на напрямок магнітного поля, як і енергія, є квантовими числами, тобто змінюються дискретно кожна відповідно до свого закону квантування.

У атомній фізиці стан електрона в атомі з різними значеннями азимутального квантового числа прий-нято позначати літерами.

l=0 – s-стан,

l=1 – p-стан,

l=2 – d-стан,

l=3 – f-стан.

Потім g, h і далі за латинською абеткою. Наприклад, якщо стан електрона 3p, то це означає, що n = 3, l = 1.

Переходи електронів за енергетичним спектром. Схему рівнів енергії (енергетичний спектр) зручно приставити у вигляді, що подано на рис. 90.

Рис. 90

Випромінювання і поглинання енергії атомом водню відбувається при переходах електрона із стану з одним значенням енергії Еn у стан з іншим значенням енергії (коротко кажуть – при переходах електрона з одного енергетичного рівня на інший).

Можливі тільки такі переходи, для яких азимутальне квантове число l змінюється на одиницю:

Δ l=±1. (8.2)

Умова (8.2) називається правилом відбору і є наслідком закону збереження моменту імпульсу при випромінюванні і поглинанні фотона.

Спектри випромінювання і поглинання. Переходи np®1s (n=2,3…) утворюють серію ліній випромінювання, яка називається серією Лаймана. Переходи електрона ns®2p, nd®2p, np®2s (n=3,4…) утворюють серію ліній випромінювання, яка називається серією Бальмера. Стан 1s – стан з мінімальною енергією – називається основним станом.

Атом поглинає (і випромінює) тільки ті фотони, енергія яких точно відповідає різниці енергії двох його рівнів. Спектр поглинання (з основного стану) 1s®np (n=2,3…).

§4. Багатоелектронні атоми

В атомах, що містять кілька електронів, кожний з електронів рухається в усередненому полі ядра і решти електронів. Енергетичні рівні електрона в такому центрально симетричному полі залежать не тільки від головного квантового числа n, але і від азимутального l, а відповідні їм хвильові функції від трьох квантових чисел

E=E_nl, f=f_nlm ,

тобто в цьому випадку знімається виродження за азимутальним квантовим числом l.

Момент імпульсу атома в цілому складається з моментів імпульсу електронів, що входять до складу атома. Додавання моментів імпульсу здійснюється за квантовими законами

,

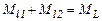де 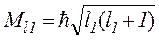; 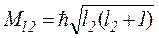– моменти імпульсів, що додаються, l₁, l₂ – їх азимутальні квантові числа. При цьому результуючий момент імпульсу

,

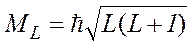де L=l₁+l₂, l₁+l₂ –1,…..½l₁ –l₂½ – азимутальне квантове число результуючого моменту імпульсу. Таким чином, результуючий момент імпульсу може набувати 2l₂+1 або 2l₁+1 (потрібно взяти менше з l_i) різних значень.

Переходи в енергетичній схемі рівнів атома підкоряються такому правилу відбору: можливі лише такі переходи, при яких момент імпульсу атома змінюється на одиницю .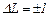

§5. Спін електрона

Якщо атоми, що випромінюють світло, помістити у магнітне поле, то лінії випромінювання в спектрі випромінювання цього атома розщеплюються на кілька окремих лінії – мультиплет. Для пояснення мультиплетної структури спектрів у 1925 р. була висунута гіпотеза про те, що електрон має власний момент імпульсу M_s, не пов’язаний з рухом електрона по орбіті. Цей власний момент імпульсу електрона було названо спіном. Спін слід вважати внутрішньою властивістю, яка притаманна електрону, подібно тому, як йому притаманні заряд і маса.

Величина власного моменту імпульсу мікрочастинки визначається квантовим числом s

.

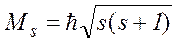Для електрона S =1/2; .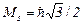

Проекція спіна на напрямок вектора індукції 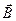магнітного поля

,

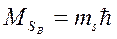де спінове квантове число електрона .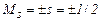

Повний момент імпульсу M_j електрона в атомі складається з орбітального M_e і спінового M_s.

M_j =M_e + M_s ,

де .

При цьому квантове число j, що визначає повний момент імпульсу електрона при 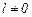, приймає два значення

,

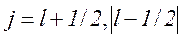а при l=0 тільки одне значення .

З механічними моментами пов’язані магнітні моменти, які взаємодіють один з одним подібно до того, як взаємодіють два контури з струмом. Енергія цієї взаємодії (яка називається спін-орбітальною взаємодією) залежить від взаємної орієнтації орбітального і спінового моментів. Отже, стани з різними квантовими числами j повинні мати різні енергії, і тому лінії випромінювання розщеплюються на мультиплети.

§6. Розподіл електронів в атомі по енергетичних рівнях

Таким чином, стан електрона в атомі характеризується чотирма квантовими числами:

1) головне n=1,2,3... (будь-яке ціле);

2) азимутальне l=0,1,2,...,n–1 – всього n значень;

3) магнітне m_l = – l,...,0,...+l – всього 2l+1значень;

4) спінове m_s=±1/2 –всього два значення.

Енергія стану в основному визначається квантовими числами n і l. Крім того, має місце слабка залежність від m_l і m_s .

Заселення енергетичних рівній, тобто розподіл електронів по станам з різними значеннями енергії, підкоряється двом принципам.

1. Принцип Паулі. В одному і тому ж атомі не може бути двох електронів, що мають однакову сукупність чотирьох квантових чисел n, l, m_l, m_s.

2. Принцип мінімуму енергії. У незбудженому стані атома електрони повинні розташовуватися на самих низьких досяжних для них енергетичних рівнях.

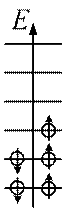
Рис. 91

На рис. 91 наведено заселеність енергетичних рівнів літію (Z=5) у незбудженому стані (тобто з мінімумом енергії). Такий стан атома має назву основного стану. Рівні розв’язані (тобто відрізняються) по квантових числах n, l, m_l. Тоді на кожному рівні (тобто у стані зі заданою енергією) знаходиться по два електрони з протилежно орієнтованими спінами, оскільки спінове квантове число приймає тільки два значення m_s=±1/2. Сукупність електронів атома, що мають однакові квантові числа n і l, утворює оболонку. Кількість електронів у оболонці 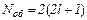. Сукупність оболонок з однаковими головними квантовими числами n утворює шар. Кількість електронів в шарі .

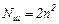Розподіл електронів по оболонках і шарах. Цей розподіл, а також позначення шарів наведено у табл. 1.

З табл. 1 видно, що елементи із зарядовим числом Z=2 (Не) і Z=10 (Ne) мають повністю заповненні шари (К – шар для Не; K і L – шари для Ne). Тому їхні хімічні властивості подібні і обидва вони відносяться до однієї групи періодичної системи (групи інертних газів). Елементи із зарядовим числом Z=3 (Li) має повністю заповнений К-шар і один електрон у 2s стані. Елемент з Z=11 (Na) має повністю заповнені K і L шари і один електрон у 3s стані. Електрон 2S для Li і 3S для Na пов’язані з ядром слабше за інших і є валентними. У зв’язку з цим хімічні властивості Na і Li подібні і вони знаходяться в одній групі періодичних систем.

Таблиця 1

n	Кількість електронів у шарі	Умовна позначка шару	Кількість електронів у оболонці
			s(l=0)	p(l=1)	d(l=2)	f(l=3)	g(l=4)
		K		–	–	–	–
		L			–	–	–
		M				–	–
		N					–
		O

Таким чином, за допомогою табл. 1 всі хімічні елементи можна розташувати по групах періодичної системи елементів.

§7. Основні види міжатомного зв’язку молекул

Сили, що утримують атоми в молекулі, обумовлені взаємодією зовнішніх електронів атомів. Електрони внутрішніх оболонок при об’єднанні атомів у молекулу залишаються у попередніх станах. Розрізняють два види зв’язку атомів в молекулах.

1. Гомеополярний (або ковалентний) зв’язок. Він здійснюється в тих молекулах, в яких частина електронів рухається навколо обох ядер. Цей зв’язок утворюється парами електронів з протилежно орієнтованими спінами (див. рис. 92)

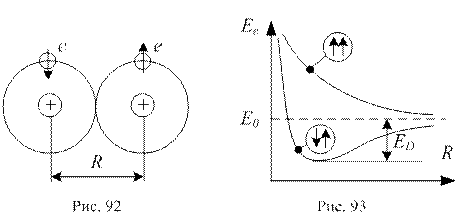
Та обставина, що утворення молекули можливе лише при наближенні атомів з антипаралельними спінами, пояснюється тим, що електронна енергія E_e, тобто енергія електронної конфігурації, залежить від відстані R між ядрами атомів у молекулі, притому у випадках паралельної і антипаралельної орієнтації спінів характер цієї залежності суттєво різний. На рис. 93 наведено такі залежності для молекул водню (Н₂).

Тільки при антипаралельній орієнтації спінів атомів у цієї залежності є мінімум і, отже, можливе утворення молекули, бо стійким станом є стан з мінімумом енергії. Граничне значення енергії Е₀ при 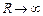, для обох кривих на рис. 93 однакове і дорівнює сумі енергії ізольованих атомів. Величина Е_D – є енергія зв’язку молекули. Вона дорівнює енергії, яку потрібно надати молекулі, щоб викликати її розподіл на атоми.

Рис. 94

2. Гетерополярний (або іонний) зв’язок. Він має місце, коли електрони в молекулі можна розділити на дві групи, кожна з яких весь час знаходиться коло одного з ядер. Електрони розподіляються так, що навколо одного з ядер утворюється надлишок електронів, а навколо іншого – їх нестача (див. рис. 94). Таким чином, молекула мовби складається з двох іонів протилежних знаків, які притягаються один до одного. Прикладами молекул з гетерополярним зв’язком є молекули NaCl, HCl та ін.

Дата добавления: 2014-01-04