Рівняння лінії рівноваги

Звичайно при розрахунках масообмінних процесів фактичні або робочі концентрації розподіляючої між фазами речовини задані. Аби знайти напрям процесу і його швидкість, необхідно знати рівноважні концентрації при робочих умовах, або залежність рівноважних концентрацій у* розподіляючої речовини в одній фазі від робочої концентрації х в іншій, тобто

y*=f(x); (8.3.1)

наприклад,

у* = т· x ⁿ; (8.3.2)

де m і n - величини, що визначаються дослідним шляхом.

Значення m залежить від фізико-хімічних властивостей системи, від температури, тиску, а часто і від концентрації розподіляючої між фазами речовини. Тому на діаграмі в координатах У - X лінії рівноваги, які описуються залежностями (8.3.1) або (8.3.2) можуть мати вигляд кривих (Рис. 8.3.1,а.)

Рис.7.3.1.Фазові діаграми Y-X: а - за рівнянням (8.3.2); б - за рівнянням (8.3) 1 - робоча лінія; 2 - лінія рівноваги.

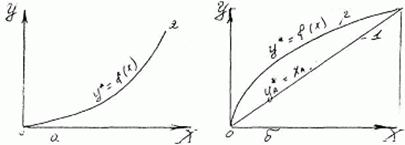
Для ідеальних систем (наприклад, розчинів) рівняння ліній рівноваги відомі. Наприклад, для ідеального розчину, якщо його температура вище критичної температури розчиняючого газу, використаємо закон Генрі, по котрому парціальний тиск розчиненого пропорційний його молярній долі в розчині:

Р* = Е·х; (8.3.3)

де р* - парціальний тиск поглинаючого газу над розчином, що знаходиться в рівновазі, при концентрації розчину х; Е - константа Генрі. Із закону Дальтона

p = P·Y (7.3.4) Тоді

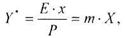(8.3.5)

де Р загальний тиск в системі.

Значення т в рівнянні (8.3.5) залежить від загального тиску і від температури. З ростом температури т збільшується зі збільшенням загального тиску значення т знижується, що призводить до збільшення розчинності газу.

При постійній температурі і тиску залежність між рівноважними значеннями у і робочими х виражається графічно прямою лінією, що проходить через початок координат, з кутом нахилу, тангенс котрого рівний т.

Закон Генрі виконується для ідеальних розчинів. Для реальних розчинів він використовується з достатньою точністю лише при сильному розбавленні. Для систем, які не підчиняються цьому закону, значення т в рівнянні (8.3.5) є змінною величиною і лінія рівноваги являє собою криву, котру будують звичайно по дослідним даним.

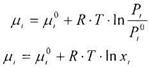
при умові рівності хімічних потенціалів:

Якщо температура ідеального розчину менше критичної температури, тобто відбувається конденсація газу то система підпорядковується закону Рауля, котрий можна отримати, співcтавивши вирази для хімічного потенціалу.

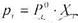(8.3.6)

З виразу (7.2.8) випливає, що парціальний тиск пару І - того компоненту над розчином рівно добутку тиску пару чистого компоненту (тобто тиск насиченого пару цього компоненту) при температурі розчину на йог мольну долю в рідкій фазі.

Для двокомпонентної суміші складу А-В вираз (8.3.4) і (8.3.6) дають зв'язок між робочими і рівноважними концентраціями:

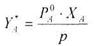(8.3.7)

Р = Р_а + Р_B = Р°_А · Х_А + Р°_В · (1 - Х_А)

Звідки

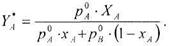
Розділивши останній вираз на р⁰_B і позначивши р⁰_А /р⁰_B через α (де α - відносна летучість компонентів), отримаємо

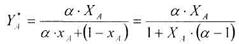(8.3.8)

Це рівняння є рівняння кривої лінії.

Часто приходиться користуватися експериментальними даними, так як закони розподілення отримані для ідеальних систем.

Знаючи рівноважні і робочі концентрації, можна знайти напрям процесу: з якої фази і в яку буде приходити розподіляюча між фазами речовина. Вважаємо, що співвідношення між робочими і рівноважними концентраціями відповідають (Рис.8.3.1,а). Якщо у > у* речовина

переходить з фази 1 в фазу 2 при цьому X < Х*. ЯкщоΥ<Υ* (при цьому Х>Х*), перехід речовини буде зворотнім - з фази 2 в фазу 1. Таким чином, розподіляємо між фазами речовина в точці контакту фаз переходить в ту фазу, робоча концентрація котрої менше рівноважної.

Крім того, знання різниці рівноважних і робочих концентрацій дозволяє визначити
рушійну силу переносу маси, що необхідно для розрахунку швидкості процесу
масопереносу.

8.4 Матеріальний баланс масообмінних процесів

В загальному вигляді матеріальний баланс масообмінних процесів може бути складений на основі наступних міркувань. Позначимо масові швидкості розподілених фаз вздовж поверхні їх розділу, виражені в кілограмах інертної речовини в годину, через G і L, а концентрація розподіляючої речовини відповідно Y кг/кг інертної речовини і Х кг/кг інертної речовини.

При Y > Y_p і відсутності, втрат в процесі взаємодії фаз при паралельних потоках вздовж

поверхні розділу концентрація Y зменшується, а X збільшується (Рис. 8.4.1). Для елемента поверхні dF маємо:

dM = G·(-dY)=L·dX ( 8.4.1)

Інтегруючи рівняння (8.4.1) в межах від початкових до кінцевих концентрацій Y_н-Y_k і Х_п - Х_к, отримаємо:

M = -G·(Y_k-Y_n) = G ·(Y_n-Y_k)=L ·X_k -X_n) (8.4.2)

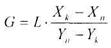(8.4.3)

З рівняння (8.4.2) отримаємо співвідношення між масовими потоками розподіляючих фаз:

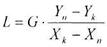(8.4.4)

Інтегруючи рівняння (8.4.1) в межах від початкової концентрації до поточних Y _п - Y і X_п - X, отримаємо:

G ·{Y_n-Y) = L · (X - X_n)

звідки

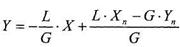(8.4.5)

або

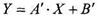(8.4.6)

де L/G - питома витрата однієї з роподіляючих фаз.

Аналогічно для противоточної взаємодії фаз можна отримати рівняння:

Y = A" ·X + B" (8.4.7)

де A" = L/G; B'' = {G ·Y_n-L·X_k)/G

З рівнянь (8.4.6) і (8.4.7) випливає, з концентрації розподіляючої речовини в фазах G і L пов'язані лінійною залежністю. Тому зручно процеси масообміну представляти графічно в координатах X - У (Рис. 8.4.2), тобто у вигляді залежностей між так званими робочими концентраціями. Рівняння прямої, що виражає залежність між робочими концентраціями, називають робочою лінією процесу.

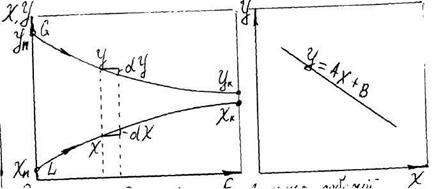
Рис. 8.4.1 До виводу рівняння робочої лінії процесу

Рис. 8.4.2 Робоча лінія процесу

Дата добавления: 2014-01-04