Рушійна сила масообмінних процесів

Рушійна сила масообмінних процесів визначається ступінню відхилення від рівноваги або "відстанню" від рівноваги. Останнє зумовлює різницю між робочою і рівноважною концентрацією або рівноважною і робочою, в залежності від того, які з них більші. При цьому очевидно, що рушійну силу можна виразити або через концентрації розподіляючої речовини в фазі G, тобто через У, або через концентрації його в фазі L, тобто через X.

На (Рис. 7.5.1.) показані можливі варіанти виразу рушійної сили масообмін них процесів
при різних напрямах переходу розподіляючої речовини.

Відповідно основне рівняння масопередачі можна записати у вигляді

dM = K_y·AY·dF (8.5.1)

або

dM=K_x·ΔX - dF (8.5.2)

Індекси біля К показують, які концентрації прийняті для виразу рушійної сили. В загальному випадку

ΔY ≠ ΔХ і К_y ≠ К_x, але, очевидно, завжди

K_y ·ΔY = K_x·ΔX (8.5.3)

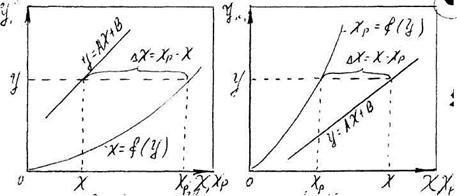
Як видно з (Рис.8.5.1), рушійна сила змінюється зі зміною робочих концентрацій, тому для всього процесу масообміну, що проходить в межах зміни концентрацій від початкових до кінцевих, повинна бути визначена середня рушійна сила(ΔΥ_m і ΔХ_т).

З урахуванням середньої рушійної сили процесу, основне рівняння масопередачі для всієї поверхні контакту фаз може бути записане у вигляді

M = K_yΔY_mF (8.5.4)

або

M = K_xΔX_mF (8.5.5)

При визначенні середньої рушійної сили можуть зустрітися два випадки:

1) залежність між рівноважними концентраціями не лінійна; для цього випадку
рівноважна концентрація визначається загальною функціональною залежністю

Y_P = f(X)

2) залежність між рівноважними концентраціями лінійна, тобто Y _р = А_р X
(де А - постійна величина).

Спочатку знайдемо середню рушійну силу для випадку Y _р =f(X)

Розглянемо зміну концентрацій X та У вздовж поверхні розподілу фаз при їх взаємодії. Для випадку Y>Y_Р при взаємодії паралельних потоків фаз поздовж поверхні розподілу Y зменшується, а X зростає (рис.8.5.2). Кожній концентрації X, згідно рівняння У_р = f(X), відповідає рівноважна концентрація Y_р. Для елемента поверхні dF рушійна сила процесу може бути виражена різницею Y-Y_р.

Для елемента поверхні dF маємо:

dM = К_у(Y-Y_p) dF; dM = G(-dY).

Співставимо ці рівняння і отримаємо:

DF = -G/K_y* dY/(Y-Y_p)

Після інтегрування в межах 0- F і Y- Y_р маємо:

Замінивши з рівняння (7.4.2) G = M/(Y-Y_P), знайдемо:

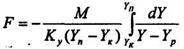(8.5.6)

або (8.5.7)

Виражаючи рушійну силу через концентрації, аналогічно попередньому отримаємо:

(8.5.8)

Порівнявши рівняння (8.5.7) і (8.5.8) з рівняннями (8.5.4) і (8.5.5.), знайдемо наступні вирази середньої рушійної сили:

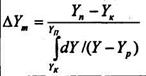(8.5.9)

(8.5.10)

Подібна структура рівнянь зберігається і в тих випадках, коли замість концентрацій використовують інші параметри, що характеризують систему: ентальпію, хімічний потенціал.

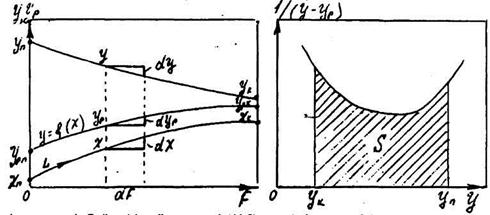
Рис.8.5.2. До визначення середньої рушійної сили дифузійних процесів.

Рис.8.5.3. До визначення середньої рушійної сили процесів графічним інтегруванням.

Рівняння (8.5.9.) і (8.5.10.) вирішують аналогічно, графічним або численним інтегруванням. Так при графічному інтегруванні знаменника дробу в рівнянні (7.5.9.) в межах концентрації Y_K - Y_n через певні інтервали для ряду значень У знаходять* відповідні їм значення X, У_р, Y- Y_р і 1/(Y- Y_p)

Потім на діаграмі в координатах Y, 1/(Y- Y_p) будують криву, як показано на рис.7.5.3. Площа під кривою обмежена ординатами У_к / У_П помножена на масштаб діаграми Syа, дає шуканий інтеграл (8.5.11.). У випадку вираження рушійної сили через концентрацію X аналогічним шляхом визначають S_xa (8.5.12.):

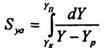(8.5.11);

(8.5.12).

Інтеграли, які знаходяться в правій частині рівнянь (7.5.11.) і (7.5.12.), широко використовуються при розрахунку масообмінної апаратури; їх позначають через т_у і m_x називають числами одиниць переносу:

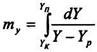(8.5.13)

(8.5.14)

Число одиниць переносу має фізичну суть, яка характеризує зміну робочої концентрації фази, що переноситься на одиницю рушійної сили.

Число одиниць переносу визначають по середній рушійній силі. З співвідношення (7.5.9.),(7.5.13.), (7.5.10.) і (7.5.14.) випливає:

(8.5.15)

(8.5.16)

Співвідношення (7.5.13) і (7.5.14) справедливі для випадку коли між робочими і рівноважними концентраціями існує залежність - як нелінійна, так і лінійна.

Для лінійної залежності, для умов Y=AХ і Y =А_РХ число одиниць переносу визначають наступним чином

(8.5.17)

(8.5.18)

Дата добавления: 2014-01-04