
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Укладач Гладун О.Є
|
|
|
|
м. Кривий Ріг
Лінійна алгебра
При розв’язуванні різних задач математики, техніки, економіки, особливо лінійних систем рівнянь, лінійних диференціальних рівнянь та їх систем, застосовують матриці, визначники та 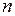 -мірні вектори.
-мірні вектори.
Матрицею називають прямокутну таблицю елементів, яка має 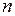 рядків та
рядків та 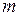 стовпців. Позначають матриці великими літерами латинського алфавіту
стовпців. Позначають матриці великими літерами латинського алфавіту 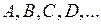 Наприклад:
Наприклад:

де 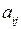 – елементи матриць, у яких індекс
– елементи матриць, у яких індекс 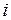 показує номер рядка, а індекс
показує номер рядка, а індекс 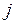 – стовпця.
– стовпця.
Якщо число рядків і стовпців матриці співпадає (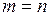 ), то така матриця називається квадратною. Так, матриця
), то така матриця називається квадратною. Так, матриця 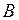 , у якої
, у якої 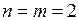 , є квадратною.
, є квадратною.
Добутком двох матриць 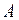 (з
(з 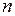 рядків та
рядків та 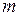 стовпчиків) та
стовпчиків) та 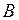 (з
(з 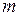 рядків та
рядків та 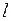 стовпчиків) називають матрицю з
стовпчиків) називають матрицю з 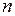 рядків та
рядків та 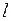 стовпчиків, у якої в
стовпчиків, у якої в 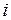 -му рядку на
-му рядку на 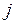 -му місці стоїть сума
-му місці стоїть сума 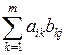 .
.
Наприклад, для матриць розмірності 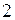 :
:
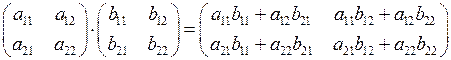 .
.
Визначником називають число, яке ставиться у відповідність квадратній матриці. Визначник (детермінант) позначають символами 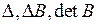 . Так, наприклад, для матриці
. Так, наприклад, для матриці 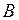 визначник будемо позначати
визначник будемо позначати
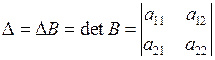 .
.
Порядком визначника називають його розмірність 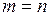 .
.
Визначником 2-го порядку є число, яке дорівнює різниці добутків елементів головної 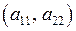 та побічної
та побічної 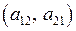 діагоналей. Так,
діагоналей. Так,
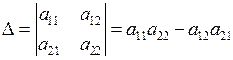 .
.
Визначники вищих порядків 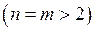 обчислюються іншим способом. Для його пояснення введемо поняття мінора та алгебраїчного доповнення визначника.
обчислюються іншим способом. Для його пояснення введемо поняття мінора та алгебраїчного доповнення визначника.
Мінором 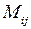 елемента
елемента 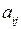 визначника
визначника 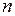 -го порядку називають визначник
-го порядку називають визначник 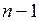 -го порядку, який одержують з визначника
-го порядку, який одержують з визначника 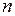 -го порядку при викреслюванні
-го порядку при викреслюванні 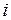 -го рядка та
-го рядка та 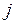 -го стовпчика.
-го стовпчика.
Алгебраїчним доповненням 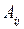 елемента
елемента 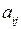 визначника
визначника 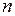 -го порядку називають мінор
-го порядку називають мінор 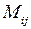 , який береться зі знаком плюс, якщо сума індексів
, який береться зі знаком плюс, якщо сума індексів 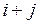 є парним числом і зі знаком мінус, якщо ця сума є непарним числом. Тобто,
є парним числом і зі знаком мінус, якщо ця сума є непарним числом. Тобто, 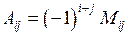 .
.
Визначником 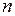 -го порядку називають число, яке, наприклад, записують у вигляді
-го порядку називають число, яке, наприклад, записують у вигляді
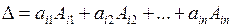 . (1)
. (1)
Вираз (1) називають розкладом визначника 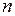 -го порядку по елементах
-го порядку по елементах 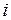 -го рядка.
-го рядка.
Для визначника 3-го порядку формула (1) має вигляд 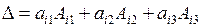 . Так, наприклад, розклад визначника 3-го порядку по елементах першого (
. Так, наприклад, розклад визначника 3-го порядку по елементах першого (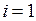 ) рядка має вигляд
) рядка має вигляд
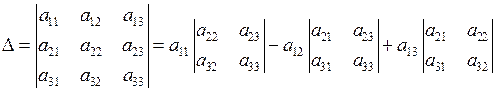 . (2)
. (2)
Приклад 1. Обчислити визначник 3-го порядку
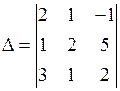 .
.
Розв’язання. Згідно формул (1), (2) визначник 3-го порядку обчислимо так:
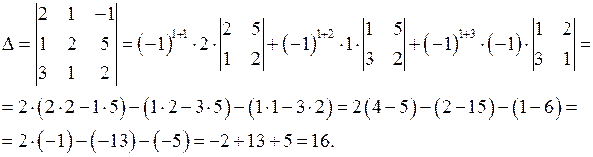
Невиродженою називають квадратну матрицю, визначник якої відмінний від нуля.
Одиничною називають квадратну матрицю, у якої по головній діагоналі знаходяться одиниці, а решта елементів дорівнюють нулю.
Оберненою до квадратної матриці 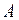 називають матрицю
називають матрицю 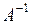 , для якої виконується умова
, для якої виконується умова 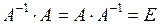 , де
, де 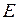 – одинична матриця. Для того, щоб для квадратної матриці існувала обернена матриця, необхідно і достатньо, щоб матриця
– одинична матриця. Для того, щоб для квадратної матриці існувала обернена матриця, необхідно і достатньо, щоб матриця 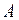 була невиродженою, тобто
була невиродженою, тобто 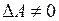 .
.
Так, для невиродженої матриці 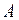 обернену до неї матрицю
обернену до неї матрицю 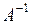 можемо записати у вигляді
можемо записати у вигляді
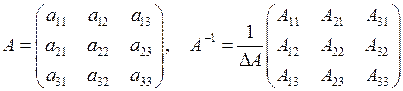 , (3)
, (3)
де 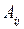 – алгебраїчне доповнення елемента
– алгебраїчне доповнення елемента 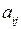 .
.
Рангом матриці називають найвищий порядок відмінного від нуля мінора цієї матриці і позначають 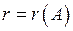 .
.
Розглянемо систему з 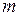 лінійних рівнянь з
лінійних рівнянь з 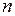 невідомими
невідомими
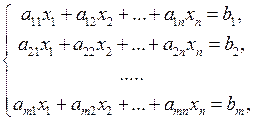 (4)
(4)
де 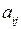 (
(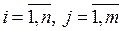 ) – коефіцієнти при невідомих
) – коефіцієнти при невідомих 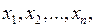
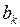 (
(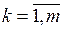 ) – вільні члени.
) – вільні члени.
Для того, щоб система лінійних рівнянь (4) була сумісною (тобто, мала розв’язок), необхідно і достатньо, щоб ранг матриці системи 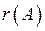 дорівнював рангу її розширеної матриці
дорівнював рангу її розширеної матриці 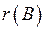 , де
, де
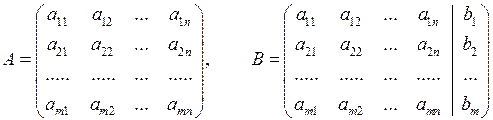 .
.
Якщо система лінійних рівнянь (4) сумісна, то вона має один або безліч розв’язків.
Розглянемо методи розв’язування лінійних рівнянь за допомогою визначників та матриць.
Правило Крамера.
Це правило можна застосувати, якщо кількість рівнянь і кількість невідомих співпадають. Для простоти викладу розглянемо систему трьох лінійних рівнянь з трьома невідомими (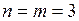 ):
):
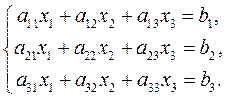 (5)
(5)
Позначимо визначники:
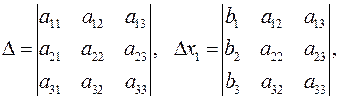
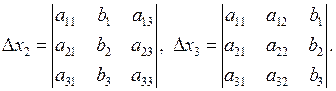
Визначник 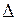 називають визначником системи і його складають з коефіцієнтів при невідомих, а у визначниках
називають визначником системи і його складають з коефіцієнтів при невідомих, а у визначниках 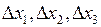 коефіцієнти при відповідних невідомих замінені вільними членами.
коефіцієнти при відповідних невідомих замінені вільними членами.
Якщо 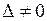 , то система (5) має єдиний розв’язок. Невідомі визначають за формулами
, то система (5) має єдиний розв’язок. Невідомі визначають за формулами
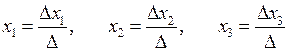 (6)
(6)
і такий спосіб визначення невідомих називають правилом Крамера.
Якщо 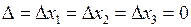 , то система (5) має безліч розв’язків, а правило Крамера застосувати не можна.
, то система (5) має безліч розв’язків, а правило Крамера застосувати не можна.
Якщо 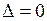 , а хоча б один із визначників
, а хоча б один із визначників 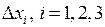 , відмінний від нуля, то система (5) несумісна.
, відмінний від нуля, то система (5) несумісна.
Приклад 2. Розв’язати систему лінійних рівнянь методом Крамера:
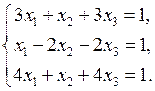
Розв’язання. Складемо і обчислимо визначники:
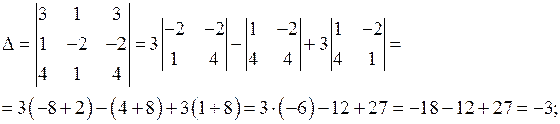
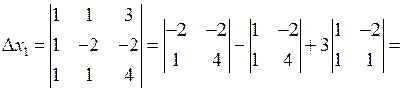
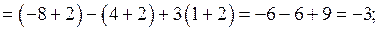
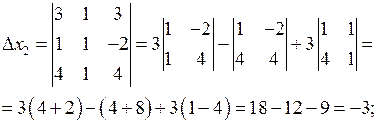
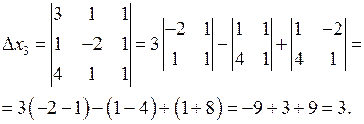
Підставимо одержані результати у формули (6). Маємо
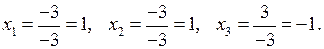
Відповідь: 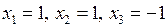 .
.
Матричний спосіб.
Матричний спосіб можна застосувати, якщо кількість рівнянь і кількість невідомих співпадають, а крім того, матриця системи має обернену.
Запишемо систему (5) у матричному вигляді. Для цього введемо матриці виду:
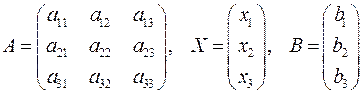 .
.
Користуючись правилом множення матриць, систему (5) запишемо у матричному вигляді
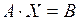 . (7)
. (7)
Розв’язок цього рівняння має вигляд
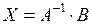 , (8)
, (8)
де 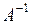 є оберненою матрицею до матриці
є оберненою матрицею до матриці 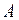 .
.
Приклад 3. Розв’язати систему лінійних рівнянь попереднього прикладу матричним способом.
Розв’язання. Перепишемо задану систему у вигляді (7). Для цього складемо матриці виду
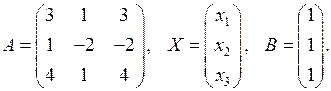
Розв’язок системи будемо шукати у вигляді (8). Необхідно знайти обернену матрицю 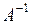 до матриці
до матриці 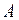 . Обернена матриця існує, бо
. Обернена матриця існує, бо 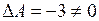 (див. приклад 2). Знайдемо алгебраїчні доповнення для кожного елемента матриці
(див. приклад 2). Знайдемо алгебраїчні доповнення для кожного елемента матриці 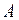 :
:
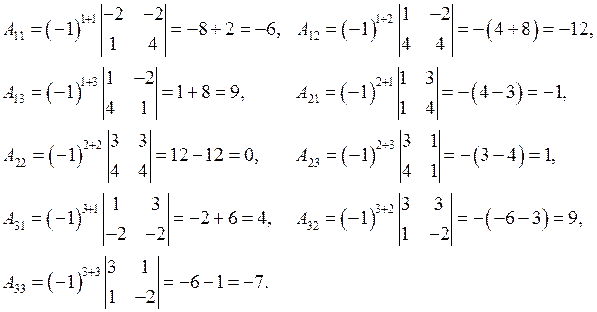
Складемо обернену матрицю згідно формули (3). Одержимо
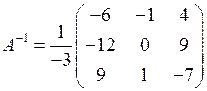 .
.
Помножимо обернену матрицю на матрицю 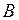 і одержимо шукану матрицю
і одержимо шукану матрицю 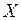 . Маємо
. Маємо
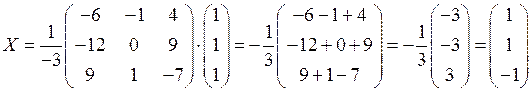 .
.
Відповідь: 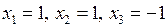 .
.
Метод Гаусса.
Для розв’язування систем лінійних рівнянь застосовують метод, який називають методом Гаусса або методом виключення змінних. Суть методу Гаусса розв’язування систем лінійних рівнянь розглянемо за допомогою матриць. Його ідея полягає у зведенні розширеної матриці системи за допомогою елементарних перетворень матриці до трикутної матриці.
Трикутною називають матрицю, у якої під головною діагоналлю всі елементи рівні нулю.
Елементарними перетвореннями матриці є такі перетворення:
1) перестановка двох рядків матриці;
2) множення всіх елементів рядка на одне і те ж число, відмінне від нуля;
3) додавання елементів якого-небудь рядка матриці, помножених на одне і те ж число, до відповідних елементів іншого рядка;
4) відкидання рядків матриці, елементами яких є нулі.
Проводячи елементарні перетворення над матрицею системи, отримують нову систему рівнянь, яка еквівалентна заданій, але з новими коефіцієнтами та вільними членами. Одержують трикутну систему рівнянь, із якої визначають невідомі.
Приклад 4. Методом Гаусса розв’язати систему лінійних рівнянь
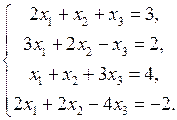
Розв’язання. Складемо розширену матрицю системи і будемо робити над нею необхідні елементарні перетворення, щоб одержати трикутну матрицю. На початку переставимо перше і третє рівняння місцями, а потім помножимо елементи першого рядка відповідно на мінус три, мінус два та мінус два і одержані результати додамо відповідно до елементів другого, третього та четвертого рядків. Аналогічно вчинимо з елементами другого, а потім третього рядків. Одержимо матрицю
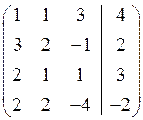 ~
~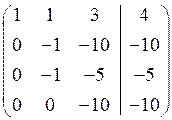 ~
~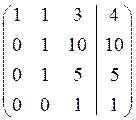 ~
~
~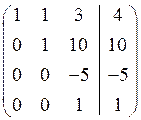 ~
~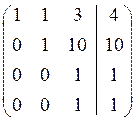 ~
~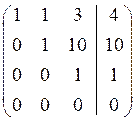 ~
~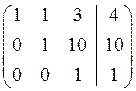 .
.
Система лінійних рівнянь матиме вигляд
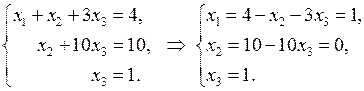
З третього рівняння 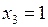 . З другого рівняння одержали
. З другого рівняння одержали 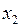 , а з першого одержуємо
, а з першого одержуємо 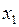 .
.
Відповідь: 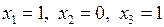 .
.
1. Елементи векторної алгебри та аналітичної геометрії
Вектором називають напрямлений відрізок простору. Вектор позначають 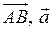 , де
, де 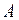 – початкова точка вектора, а
– початкова точка вектора, а 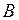 – кінцева.
– кінцева.
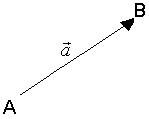 Якщо точки
Якщо точки 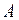 та
та 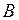 задані своїми координатами
задані своїми координатами 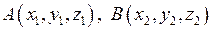 , то проекції вектора на відповідні осі координат будуть дорівнювати різниці відповідних координат:
, то проекції вектора на відповідні осі координат будуть дорівнювати різниці відповідних координат: 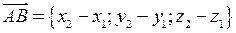 .
.
Ортами (одиничними векторами) називають три взаємно-перпендикулярних вектори, довжини яких дорівнюють одиниці, їх позначають через 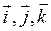
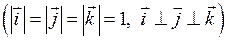 . Тоді вектори
. Тоді вектори 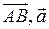 можна записати через проекції (координати) у вигляді
можна записати через проекції (координати) у вигляді
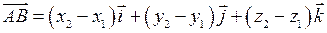 , (9)
, (9)
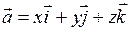 . (10)
. (10)
Довжину (модуль) вектора можна знайти за формулами:
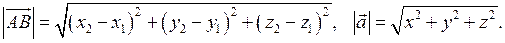 (11)
(11)
Скалярним добутком двох векторів 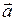 і
і 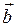 називають число, яке дорівнює добутку модулів цих векторів на косинус кута між ними. Тобто
називають число, яке дорівнює добутку модулів цих векторів на косинус кута між ними. Тобто
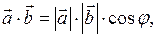 (12)
(12)
або
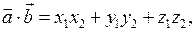 (13)
(13)
якщо вектори задані координатами 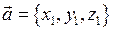 і
і 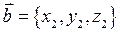 . З формули (12), з урахуванням формул (11) і (13) випливає, що косинус кута між двома векторами можна обчислити так:
. З формули (12), з урахуванням формул (11) і (13) випливає, що косинус кута між двома векторами можна обчислити так:
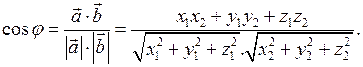 (14)
(14)
Векторним добутком двох векторів називають третій вектор, який задовольняє умовам:
1) довжина вектора чисельно дорівнює площі паралелограма, який побудований на заданих векторах;
2) вектор перпендикулярний до площини векторів-множників;
3) вектор направлений в той бік, що якщо дивитися з його кінця, то рух від першого вектора-множника до другого буде здійснюватися проти годинникової стрілки.
Векторний добуток позначають у вигляді 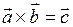 , або
, або
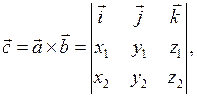 (15)
(15)
якщо вектори 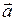 та
та 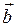 задані координатами.
задані координатами.
Рівняння прямої, що проходить через точки 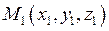 і
і 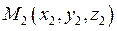 простору можна записати за формулою
простору можна записати за формулою
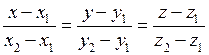 . (16)
. (16)
Задача 1. Дано координати вершин піраміди 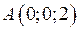 ,
, 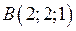 ,
, 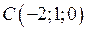 та
та 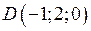 . Знайти:
. Знайти:
1) довжину ребра 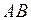 ;
;
2) написати рівняння ребра 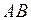 ;
;
3) обчислити кут між ребрами 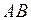 і
і 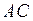 ;
;
4) обчислити площу основи 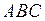 ;
;
5) зробити схематичний малюнок піраміди.
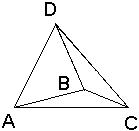 Розв’язання. Зробимо схематичний малюнок піраміди (Рис. 1).
Розв’язання. Зробимо схематичний малюнок піраміди (Рис. 1).
1) Знайдемо довжину ребра 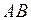 за формулою (11). Одержимо
за формулою (11). Одержимо 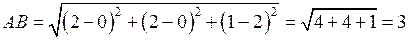 .
.
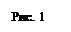 2) За формулою (16) напишемо рівняння ребра
2) За формулою (16) напишемо рівняння ребра 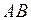 :
:
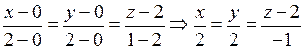 .
.
3) Для обчислення косинуса кута між ребрами 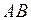 і
і 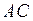 знайдемо координати векторів:
знайдемо координати векторів: 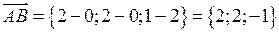 і
і 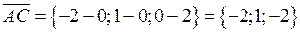 . Тоді в силу формули (14) одержимо
. Тоді в силу формули (14) одержимо
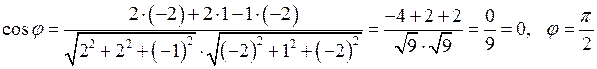 .
.
4) Площа основи 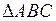 дорівнює половині площі паралелограма, який побудований на векторах
дорівнює половині площі паралелограма, який побудований на векторах 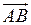 та
та 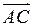 . Тобто
. Тобто 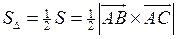 . Векторний добуток векторів
. Векторний добуток векторів 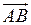 та
та 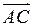 обчислимо за формулою (15). Тоді
обчислимо за формулою (15). Тоді
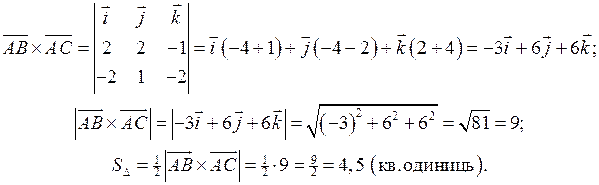
2. Криві другого порядку
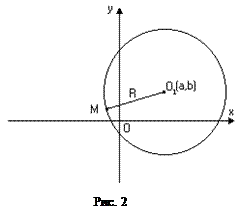 Колом називається множина точок площини, рівновіддалених від однієї точки
Колом називається множина точок площини, рівновіддалених від однієї точки 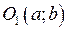 , яка називається центром. Канонічне рівняння кола має вигляд
, яка називається центром. Канонічне рівняння кола має вигляд
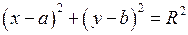 або
або 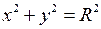 , (17)
, (17)
коли центр кола співпадає з початком координат. 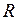 – радіус кола (Рис. 2).
– радіус кола (Рис. 2).
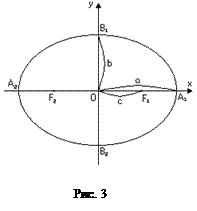 Еліпсом називається множина всіх точок площини, сума відстаней від яких до двох фіксованих точок, які називаються фокусами, є величина стала (Рис. 3). Канонічне рівняння еліпса має вигляд
Еліпсом називається множина всіх точок площини, сума відстаней від яких до двох фіксованих точок, які називаються фокусами, є величина стала (Рис. 3). Канонічне рівняння еліпса має вигляд
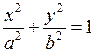 , де
, де 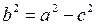 . (18)
. (18)
Величини 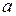 і
і 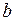 – півосі еліпса, а фокуси мають такі координати:
– півосі еліпса, а фокуси мають такі координати: 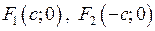 . Відношення
. Відношення 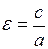 характеризує форму еліпса і називається його ексцентриситетом.
характеризує форму еліпса і називається його ексцентриситетом.
Гіперболою називається множина всіх точок площини, для яких модуль різниці відстаней кожної з них до двох фіксованих точок площини, які називаються фокусами, є величина стала (Рис. 4). Канонічне рівняння гіперболи має вигляд
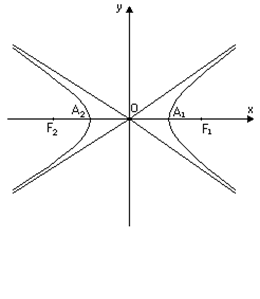
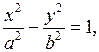 де
де 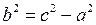 . (19)
. (19)
|
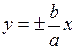 називаються асимптотами гіперболи. Гілки гіперболи наближаються до даних асимптот.
називаються асимптотами гіперболи. Гілки гіперболи наближаються до даних асимптот.
|
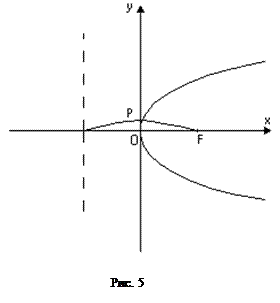
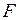 , яка називається фокусом, і даної прямої, яка називається директрисою (Рис. 5). Канонічне рівняння параболи має вигляд
, яка називається фокусом, і даної прямої, яка називається директрисою (Рис. 5). Канонічне рівняння параболи має вигляд
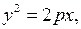 (20)
(20)
де величина 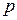 називається параметром параболи.
називається параметром параболи.
Зауваження. Якщо фокальна вісь параболи буде співпадати з віссю 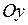 , то рівняння параболи має вигляд
, то рівняння параболи має вигляд
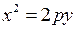 . (21)
. (21)
Приклад 5. 1) Знайти координати центра і величину радіуса кола 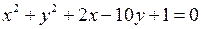 .
.
2) Для гіперболи 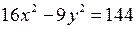 знайти величини півосей, координати фокусів, ексцентриситет та написати рівняння її асимптот.
знайти величини півосей, координати фокусів, ексцентриситет та написати рівняння її асимптот.
Розв’язання. 1) Запишемо рівняння кола у канонічному вигляді (17), виділяючи повні квадрати відносно кожної змінної величини. Одержимо
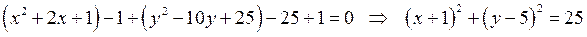 .
.
Центр кола лежить в точці 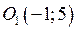 , а радіус
, а радіус 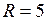 .
.
2) Якщо поділимо почленно рівняння гіперболи на  , то одержимо канонічне рівняння вигляду (19):
, то одержимо канонічне рівняння вигляду (19):
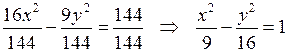 , де
, де 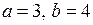 .
.
Значення 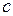 знайдемо з рівняння
знайдемо з рівняння 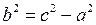 . Тут
. Тут 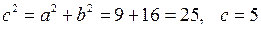 .
.
Фокуси мають координати: 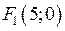 і
і 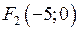 , а ексцентриситет
, а ексцентриситет 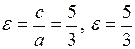 .
.
Рівняння асимптот відповідно є 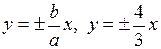 .
.
3. Границя функції
Розглянемо деякі основні поняття функції однієї змінної, яку будемо позначати аналітично 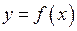 .
.
Одним із найважливіших понять математичного аналізу є поняття границі функції.
Границею функції 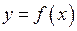 при
при 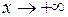 називають число
називають число 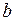 , якщо яке б не було додатне число
, якщо яке б не було додатне число 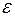 , можна знайти такий номер
, можна знайти такий номер  , що для всіх
, що для всіх 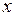 , більших
, більших  , виконується нерівність
, виконується нерівність 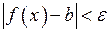 .
.
Границю функції записують у вигляді
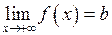 .
.
Границею функції 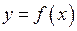 при
при 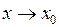 називають число
називають число 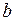 , якщо для довільного додатного
, якщо для довільного додатного 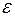 знайдеться таке
знайдеться таке 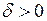 , що якщо виконується нерівність
, що якщо виконується нерівність 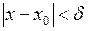 , то матиме місце також нерівність
, то матиме місце також нерівність 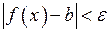 .
.
У цьому випадку границю функції записують у такому вигляді:
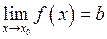 .
.
Нескінченно малою називають функцію, границя якої дорівнює нулю.
Нескінченно великою називають функцію 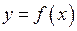 , якщо починаючи з деякого номера
, якщо починаючи з деякого номера  значення функції для всіх
значення функції для всіх 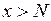 стає більшим за будь-яке велике значення
стає більшим за будь-яке велике значення 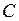 , тобто
, тобто 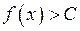 при
при 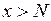 .
.
Оберненою функцією до нескінченно малої є нескінченно велика функція і навпаки. Символічно це твердження (не строго математично) можемо записати так: 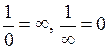 .
.
Основними властивостями границі функції є такі властивості:
1) 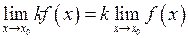 ;
;
2) 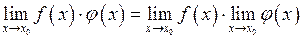 ;
;
3) 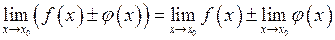 ;
;
4) 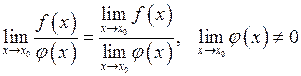 .
.
При обчисленні границі функції під знак границі підставляють значення 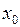 (
(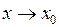 ) замість
) замість 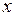 .
.
Приклад 6. Обчислити границю функції
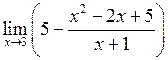 .
.
Розв’язання. Замість 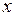 підставимо число
підставимо число 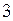 під знаком границі. Одержимо
під знаком границі. Одержимо
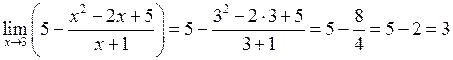 .
.
Приклад 7. Обчислити границю функції
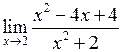 .
.
Розв’язання. Підставимо число 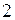 замість
замість 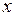 і одержимо
і одержимо
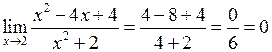 .
.
Приклад 8. Обчислити границю функції
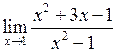 .
.
Розв’язання. Підставимо число 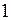 замість
замість 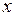 і одержимо:
і одержимо:
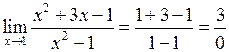 .
.
В силу четвертої властивості границю функції не обчислюють. Але будемо виходити із визначення нескінченно малої та великої функцій і зв’язку між ними. Тоді вираз 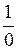 позначили “
позначили “ ”. Це знак границі нескінченно великої функції. Тобто:
”. Це знак границі нескінченно великої функції. Тобто:
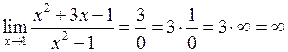 .
.
Часто при обчисленні границь виникають невизначеності виду 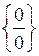 ;
; 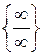 ;
; 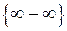 ;
; 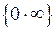 ;
; 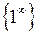 ;
; 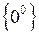 ;
; 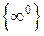 . Для того щоб розкрити ці невизначеності, необхідно зробити деякі алгебраїчні перетворення виразів, які є під знаком границі, або ж застосувати так звані “визначні” границі. Основними з них є такі:
. Для того щоб розкрити ці невизначеності, необхідно зробити деякі алгебраїчні перетворення виразів, які є під знаком границі, або ж застосувати так звані “визначні” границі. Основними з них є такі:
1) 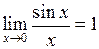 – перша “визначна” границя;
– перша “визначна” границя;
2)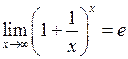 ,
, 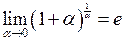 – другі “визначні” границі, а число
– другі “визначні” границі, а число 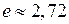 і називається сталою Ейлера.
і називається сталою Ейлера.
Приклад 9. Обчислити границю функції
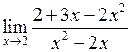 .
.
Розв’язання.
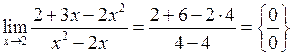 .
.
Для розкриття невизначеності виду 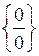 розкладемо на множники чисельник і знаменник виразу, а потім скоротимо на вираз
розкладемо на множники чисельник і знаменник виразу, а потім скоротимо на вираз 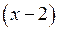 . Одержимо
. Одержимо
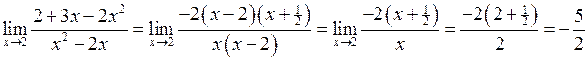 .
.
Приклад 10. Знайти границю функції
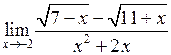 .
.
Розв’язання. Після підстановки 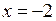 одержимо невизначеність виду
одержимо невизначеність виду 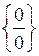 :
:
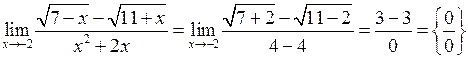 .
.
Для того, щоб вираз, який знаходиться під знаком границі, скоротити на 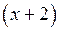 , домножимо чисельник і знаменник дробу на спряжене чисельника. Одержимо:
, домножимо чисельник і знаменник дробу на спряжене чисельника. Одержимо:
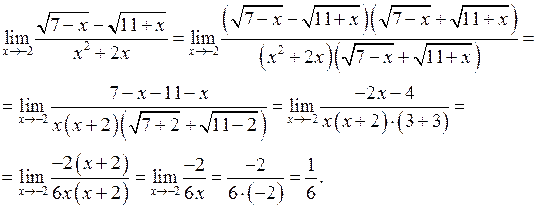
Еквівалентними називаються дві нескінченно малі функції, границя відношення яких при 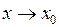 дорівнює одиниці. Еквівалентність функцій позначають знаком “~”, тобто
дорівнює одиниці. Еквівалентність функцій позначають знаком “~”, тобто 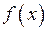 ~
~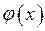 . В силу першої “визначної” границі можна записати
. В силу першої “визначної” границі можна записати 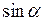 ~
~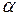 . Еквівалентними при
. Еквівалентними при 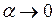 будуть також функції:
будуть також функції: 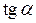 ~
~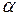 ,
, 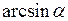 ~
~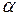 ,
, 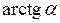 ~
~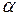 та інші.
та інші.
Приклад 11. Знайти границю виразу
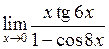 .
.
Розв’язання.
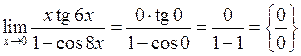 .
.
У даному випадку для розкриття невизначеності слід використати першу “визначну” границю, або еквівалентність функцій:
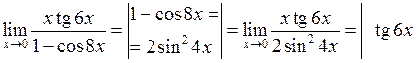 ~
~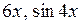 ~
~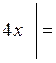
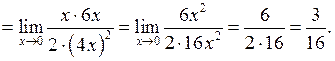
Приклад 12. Обчислити границю виразу
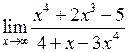 .
.
Розв’язання. У цьому випадку одержуємо невизначеність виду 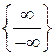 . Звертаємо увагу тільки на найвищий степінь
. Звертаємо увагу тільки на найвищий степінь 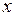 (
(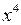 ). Розділимо вираз почленно на найвищий степінь
). Розділимо вираз почленно на найвищий степінь 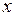 і перейдемо до обчислення нескінченно малих функцій. Маємо:
і перейдемо до обчислення нескінченно малих функцій. Маємо:
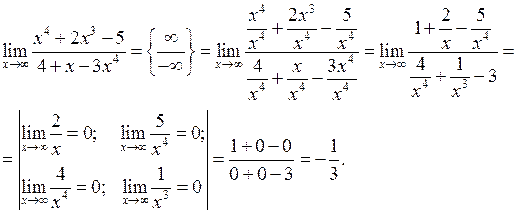
4. Диференціальне числення функцій однієї змінної
Другим важливим поняттям математичного аналізу є поняття похідної функції.
Похідною функції 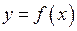 , неперервної в точці
, неперервної в точці 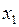 , називають границю відношення приросту функції
, називають границю відношення приросту функції 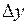 до приросту аргументу
до приросту аргументу 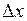 , коли
, коли 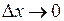 , тобто
, тобто
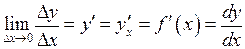 ,
,
де 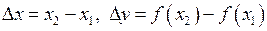 .
.
Геометричним змістом похідної є: значення похідної в точці рівне значенню кутового коефіцієнта, який утворюється між дотичною і віссю 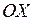 , коли дотична проведена до графіка функції
, коли дотична проведена до графіка функції 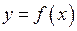 в заданій точці.
в заданій точці.
Якщо функція має похідну, то вона називається диференційованою.
Основні правила диференціювання:
1) 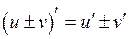 ; 2)
; 2) 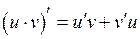 ;
;
3) 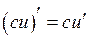 ; 4)
; 4) 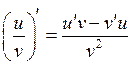 .
.
Якщо функція 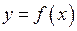 , а
, а 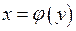 є оберненою функцією до неї, то
є оберненою функцією до неї, то
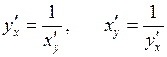 .
.
Якщо функція 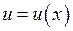 має похідну
має похідну 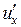 в точці
в точці 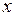 , а функція
, а функція 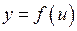 має похідну
має похідну 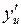 у відповідній точці
у відповідній точці 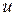 , то складена функція
, то складена функція 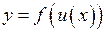 в даній точці
в даній точці 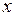 має похідну
має похідну 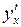 , яка обчислюється за формулою
, яка обчислюється за формулою 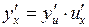 .
.
Таблиця похідних:
1. 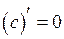 ;
;
2. 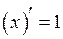 ;
;
3. 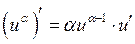 ;
;
4. 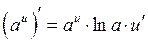 ;
;
5. 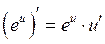 ;
;
6. 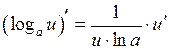 ;
;
7. 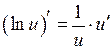 ;
;
8. 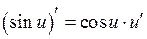 ;
;
9. 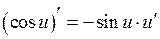 ;
;
10. 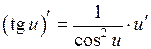 ;
;
11. 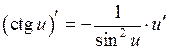 ;
;
12. 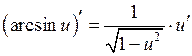 ;
;
13. 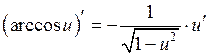 ;
;
14. 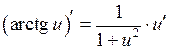 ;
;
15. 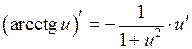 ;
;
16. 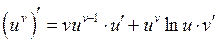 .
.
Приклад 13. Знайти похідну функції
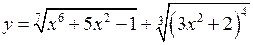 .
.
Розв’язання. Перепишемо функцію у такому вигляді:
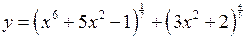 .
.
В силу формули 3 з таблиці похідних та правила диференціювання суми можемо записати
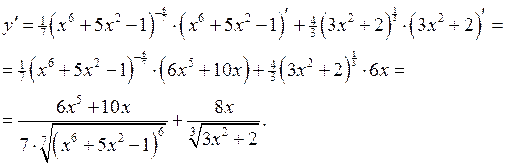
Приклад 14. Знайти похідну функції
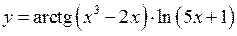 .
.
Розв’язання. При диференціюванні функції застосуємо правило диференціювання добутку двох функцій та формули 7 і 14 із таблиці похідних. Одержимо
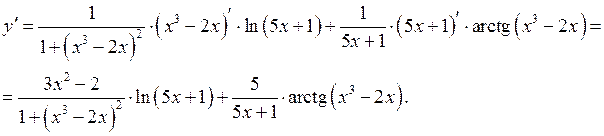
Приклад 15. Знайти похідну функції
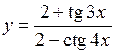 .
.
Розв’язання. Застосуємо правило диференціювання дробу та формули 10 і 11 з таблиці похідних. Одержимо
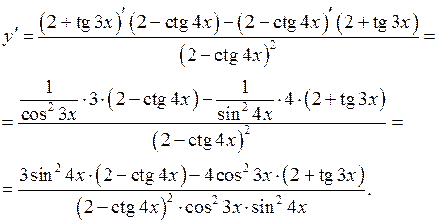
Приклад 16. Знайти похідну функції
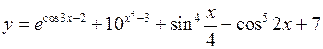 .
.
Розв’язання. Застосуємо правило диференціювання суми та необхідні формули з таблиці похідних. Одержуємо
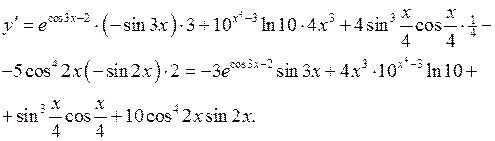
Похідною 2-го порядку називають похідну від похідної 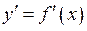 , якщо вона існує і позначають
, якщо вона існує і позначають
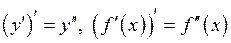 .
.
Похідною n -го порядку називають першу похідну від похідної 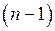 -го порядку і позначають
-го порядку і позначають
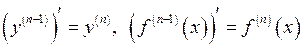 . (22)
. (22)
Приклад 17. Знайти похідну 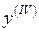 від функції
від функції 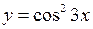 .
.
Розв’язання. З формули (22) випливає, що для знаходження похідної четвертого порядку необхідно знайти похідну третього порядку, похідна 3-го порядку знаходиться як похідна від похідної 2-го порядку, а похідна 2-го порядку знаходиться як похідна від похідної першого порядку. Будемо знаходити послідовно похідні 1-го, 2-го, 3-го та 4-го порядків. Маємо:
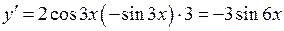 ;
; 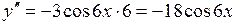 ;
;
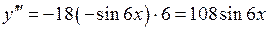 ;
; 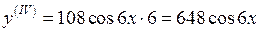 .
.
5. Дослідження функцій за допомогою похідних
Похідна функції має широке застосування при розв’язуванні різних задач математики, фізики, техніки та економіки. Так, наприклад, за допомогою похідної можна обчислити границю функції, знайти екстремум функції, інтервали монотонності, точки перегину функції та інше.
Інтервалами монотонності функції називаються ті інтервали, на яких функція або тільки зростає, або тільки спадає або залишається сталою.
Якщо неперервна на сегменті 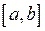 функція
функція 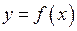 має в кожній точці цього сегмента додатну похідну, то вона зростає на цьому сегменті, а якщо від’ємну похідну, то вона спадає на цьому сегменті.
має в кожній точці цього сегмента додатну похідну, то вона зростає на цьому сегменті, а якщо від’ємну похідну, то вона спадає на цьому сегменті.
Функція 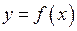 має максимум в точці
має максимум в точці 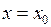 , якщо для довільних точок із її околу виконується умова
, якщо для довільних точок із її околу виконується умова 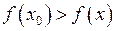 і має мінімум в точці, якщо виконується така умова:
і має мінімум в точці, якщо виконується така умова: 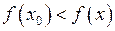 .
.
Максимум і мінімум функції називають екстремуми функції.
Необхідною умовою існування екстремуму в точці 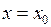 диференційовної функції
диференційовної функції 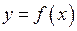 є рівність нулю її похідної:
є рівність нулю її похідної: 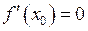 .
.
 Критичними або стаціонарними точками неперервної функції
Критичними або стаціонарними точками неперервної функції 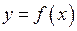 є ті точки, в яких її похідна дорівнює нулю або не існує.
є ті точки, в яких її похідна дорівнює нулю або не існує.
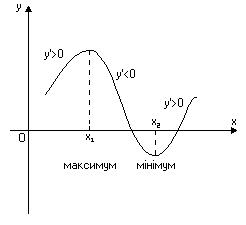
Достатньою умовою існування екстремуму в точці 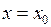 для диференційованої функції
для диференційованої функції 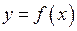 є зміна знака похідної при переході через цю точку. Так при зміні знака з “+” на “–” в точці
є зміна знака похідної при переході через цю точку. Так при зміні знака з “+” на “–” в точці 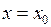 функція має максимум, а з “–” на “+” – мінімум (Рис. 6).
функція має максимум, а з “–” на “+” – мінімум (Рис. 6).
 Вгнутим називається графік диференційованої функції
Вгнутим називається графік диференційованої функції 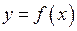 в інтервалі
в інтервалі 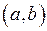 , якщо він знаходиться вище довільної його дотичної на цьому інтервалі.
, якщо він знаходиться вище довільної його дотичної на цьому інтервалі.
|
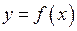 в інтервалі
в інтервалі 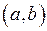 , якщо він знаходиться нижче довільної його дотичної на цьому інтервалі.
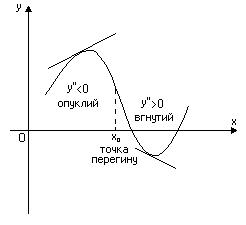
, якщо він знаходиться нижче довільної його дотичної на цьому інтервалі.Точкою перегину неперервної функції називається та точка, яка відділяє вгнутість від опуклості її графіка (Рис. 7).
Якщо друга похідна функції 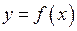 для всіх
для всіх 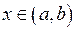 від’ємна (
від’ємна (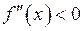 ), то тут графік функції опуклий, а якщо
), то тут графік функції опуклий, а якщо 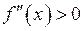 – вгнутий.
– вгнутий.
Необхідною умовою існування точки перегину графіка функції є рівність нулю її другої похідної: 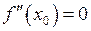 в даній точці
в даній точці 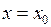 .
.
Точка 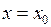 , в якій
, в якій 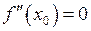 , називається критичною точкою другого порядку для функції
, називається критичною точкою другого порядку для функції 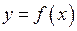 .
.
Достатньою умовою існування точки перегину графіка неперервної функції є зміна знаку другої похідної при переході через точку 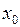 .
.
Асимптотою графіка функції 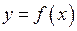 називається пряма лінія, до якої графік функції наближається на нескінченності.
називається пряма лінія, до якої графік функції наближається на нескінченності.
Вертикальною асимптотою є пряма 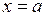 , якщо виконується умова
, якщо виконується умова 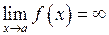 .
.
Для функції 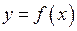 вертикальні асимптоти існують в її точках розриву другого роду.
вертикальні асимптоти існують в її точках розриву другого роду.
Похилу асимптоту шукають у вигляді 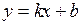 , а параметри
, а параметри 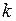 і
і 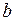 шукають за формулами:
шукають за формулами:
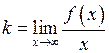 ,
, 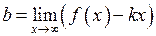 . (23)
. (23)
Якщо хоча б одна границя не існує, то похила асимптота відсутня.
При знаходженні границь (23) інколи зручно використовувати правило Лопіталя: якщо границя відношення двох функцій 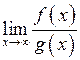 є невизначеністю виду
є невизначеністю виду 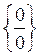 або
або 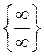 , то її можна знаходити за формулою
, то її можна знаходити за формулою
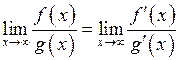 ,
,
якщо остання границя існує.
Приклад 18. Знайти найбільше та найменше значення функції 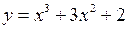 на відрізку
на відрізку 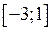 .
.
Розв’язання. Функція може досягати свого найбільшого та найменшого значення або на кінцях відрізка, або у критичних точках, якщо вони знаходяться у середині відрізка. Знайдемо критичні точки функції і розглянемо тільки ті, які потрапляють в інтервал 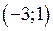 .
.

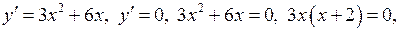
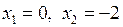 .
.
Обчислимо значення функції у критичних точках та на кінцях відрізка. Одержимо:
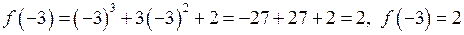 ;
;
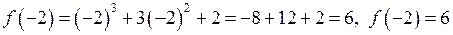 ;
;
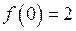 ;
; 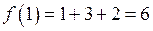 .
.
Відповідь: 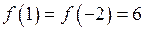 – найбільше значення функції;
– найбільше значення функції; 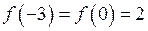 – найменше значення функції на відрізку.
– найменше значення функції на відрізку.
Приклад 19. Провести повне дослідження функції 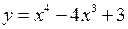 та побудувати її графік.
та побудувати її графік.
Розв’язання. 1) Знайдемо область визначення функції: 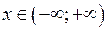 .
.
2) У графіка цієї функції відсутні асимптоти. Якщо функція неперервна, то відсутні вертикальні асимптоти. При знаходженні похилих асимптот 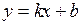 параметр
параметр 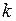 не дорівнює скінченному числу:
не дорівнює скінченному числу:
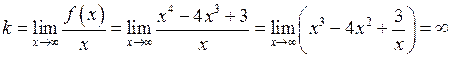 .
.
3) Знайдемо інтервали монотонності та критичні точки функції за допомогою першої похідної.
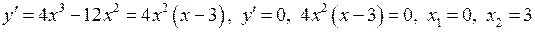 .
.
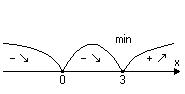 Одержані точки розбивають область визначення функції на такі інтервали:
Одержані точки розбивають область визначення функції на такі інтервали: 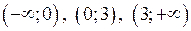 . Знайдемо знак похідної в кожному з інтервалів.
. Знайдемо знак похідної в кожному з інтервалів.
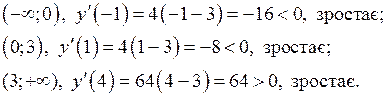
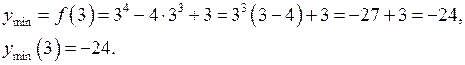
4) Знайдемо інтервали вгнутості та точки перегину графіка функції за допомогою похідної другого порядку.
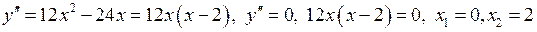 .
.
Критичні точки другого порядку 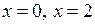 розбивають область визначення функції на інтервали вгнутості. Знайдемо знак другої похідної у кожному з них.
розбивають область визначення функції на інтервали вгнутості. Знайдемо знак другої похідної у кожному з них.
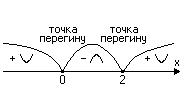
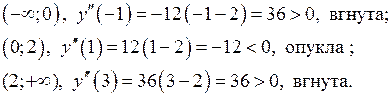
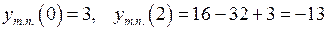 .
.
 Точки перегину функції мають координати:
Точки перегину функції мають координати: 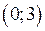 і
і 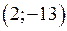 .
.
5) Знайдемо точки перетину функції з осями координат: при 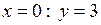 ; при
; при 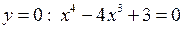 . Для рівняння
. Для рівняння 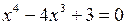 можна методом підбору знайти один корінь
можна методом підбору знайти один корінь 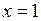 .
.
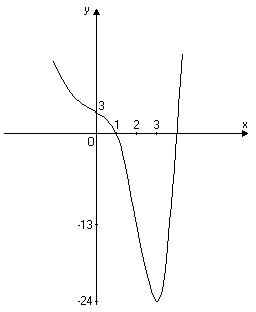
6) Побудуємо схематично графік функції (рис. 8).
 Приклад 20. Провести повне дослідження функції
Приклад 20. Провести повне дослідження функції 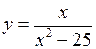 та побудувати її графік.
та побудувати її графік.
Розв’язання. 1) Знайдемо область визначення функції. Необхідно знайти ті точки, в яких знаменник дробу дорівнює нулю і виключити їх. Одержимо 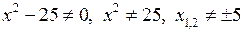 . Функція визначена в інтервалах
. Функція визначена в інтервалах 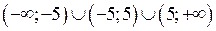 .
.
2) Знайдемо асимптоти графіка функції.
а) Вертикальні асимптоти будемо шукати в точках розриву функції. Одержимо
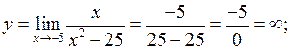
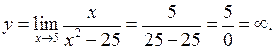
Прямі 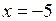 та
та 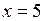 є вертикальними асимптотами функції.
є вертикальними асимптотами функції.
б) Похилі асимптоти будемо шукати у вигляді 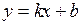 , а невідомі параметри
, а невідомі параметри 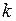 і
і 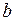 визначимо за формулами (23). Одержимо
визначимо за формулами (23). Одержимо
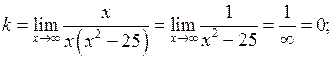
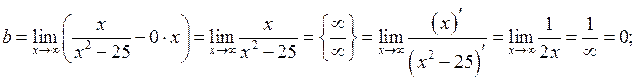
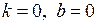 , тоді
, тоді 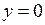 – вісь
– вісь 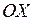 – похила асимптота.
– похила асимптота.
3) Знайдемо інтервали монотонності та критичні точки функції. Для цього знайдемо першу похідну функції. Маємо:
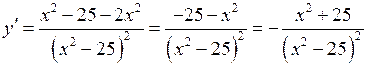 ;
;
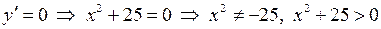 .
.
Тоді 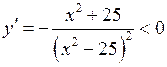 для всіх
для всіх 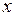 із області неперервності.
із області неперервності.
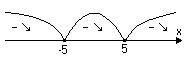 Тобто функція спадна на кожному інтервалі області визначення.
Тобто функція спадна на кожному інтервалі області визначення.
4) Знайдемо інтервали вгнутості та точки перегину графіка функції. Для цього знайдемо другу похідну.
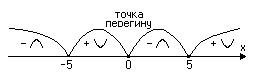
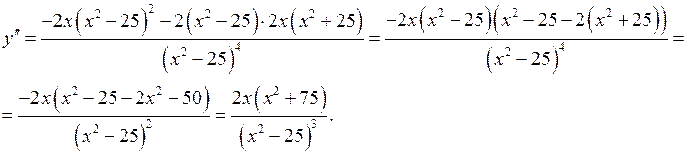 Прирівняємо
Прирівняємо 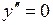 . Одержимо
. Одержимо 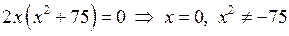 ;
; 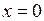 – критична точка.
– критична точка.
Знайдемо знак другої похідної в кожному з інтервалів 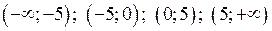 .
.
Маємо 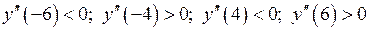 .
.
На інтервалах 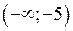 та
та 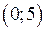 графік опуклий, а на інтервалах
графік опуклий, а на інтервалах 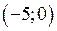 та
та 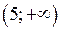 – вгнутий. Точка
– вгнутий. Точка 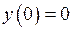 є точкою перегину графіка функції.
є точкою перегину графіка функції.
5) Знайдемо точки перетину графіка функції з осями координат: при 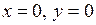 , при
, при 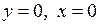 . Інших точок не існує.
. Інших точок не існує.
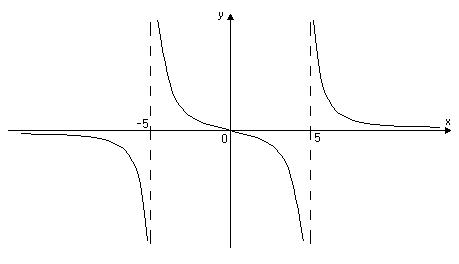
6) Використовуючи результати досліджень, побудуємо графік функції (Рис. 9).
|
|
|
Зауваження. Часто при побудові графіка функції знаходять парність функції. Тобто перевіряють
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 446; Нарушение авторских прав?; Мы поможем в написании вашей работы!