Розрахунок збитків

Розглянемо терміновий контракт страхування життя людини в віці 40 років (термін: 10 років; застрахована сума: , яка виплачується наприкінці року смерті; премія 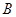, яка виплачується щорічно на початку року, поки людина жива, але не більше 10 років). Збиток 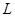страхувальника визначається формулою

, (2.1)

де 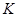позначає вкорочений час майбутнього життя людини (40). Випадкова змінна 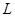має дискретний розподіл, що сконцентрований в 11 точках:

,

. (2.2)

Знайдемо чисту річну премію. З (1.1) отримаємо умову

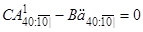, (2.3)

звідки знаходимо

. (2.4)

В якості ілюстрації, візьмемо 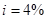і припустимо, що смертність (40) відповідає закону Де Муавра з кінцевим віком. Маємо

,

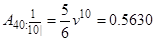, (2.5)

тому

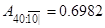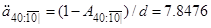, . (2.6)

З (2.4) отримаємо чисту річну премію

. (2.7)

Страхувальник не може сподіватися, що його виплати будуть відповідати чистим преміям: повинна бути деяка надбавка безпеки, що відображає застрахований ризик. Далі буде описаний метод знаходження премій, що враховує вхідний ризик.

Премії будуть визначатися за допомогою функції корисності : це функція, яка задовольняє умови , 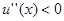і вимірює корисність, яку страхувальник отримує з суми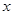. Більш точно, ми припустимо, що функція корисності експоненціальна

, (2.8)

де параметр вимірює ступінь ризику страхувальника. Умова (1.1) замінюється в цьому випадку на

, (2.9)

тобто премії тепер потрібно визначити так, щоб очікувана корисність збитку дорівнювала нулю. При функції корисності, яка визначається співвідношенням (2.8), річна премія повинна задовольняти рівняння

. (2.10)

З (2.2) при и отримуємо

. (2.11)

Візьмемо, наприклад, 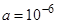. Річні премії з (2.11) протабульовані нижче

Застрахована сума	Річна премія	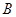Процент від чистої премії
		104%
		123%
		153%
		250%
		430%
		764%
		1248%

Очевидно, тепер премія не пропорційна застрахованій сумі, як було у випадку чистої премії, але зростає зі збільшенням . Це логічно: Застрахована сума в 100000 одиниць представляє собою малий ризик для страхувальника, тому надбавка безпечності (4%) невелика. Але застрахована сума в розмірі 5 мільйонів, з іншої сторони, представляє істотний ризик (принаймні при 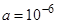), що, теоретично, робить надбавку безпеки 1148% прийнятною.

На перший погляд, цей результат суперечить практиці страхування, оскільки премії як правило пропорційні застрахованій сумі. Цю суперечність можна розв’язати таким підходом: нехай страхувальник вилучає 250% чистої премії для всіх значень : тоді контракти з застрахованою сумою, яка перевищує 2 мільйони, потребують перестрахування; контракти з меншою застрахованою сумою переоцінені, що компенсується порівняно високою, але фіксованою ціною цих контрактів.

Чисті премії відіграють більшу роль в практиці страхування. Більше того, вони як правило обраховуються при песимістичних припущеннях відносно майбутніх процентної ставки і смертності, включаючи, таким чином, неявну надбавку безпеки.

Дата добавления: 2014-01-04