Випадок простих видів страхування

3.1 Безтермінове і термінове страхування

Розглянемо контракт безтермінового страхування життя з застрахованою сумою 1, яка виплачується наприкінці року смерті, що забезпечується чистими річними преміями, які ми позначимо 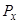. Збиток страхувальника дорівнює

. (3.1)

З (1.1) маємо, що

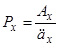. (3.2)

Записуючи оплату премій у вигляді різниці двох безтермінових аннуітетів (один починається в момент 0, другий – в момент 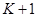), отримуємо

. (3.3)

Тому

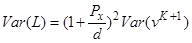. (3.4)

Це рівняння показує, що страхувальник стоїть перед великим ризиком, якщо контракт передбачає чисті річні премії замість чистої одиночної премії.

За допомогою рівняння (3.2) можна отримати дві формули для 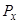, яким можна дати корисну інтерпретацію. Поділивши рівняння (2.8) лекції 4 на 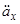, отримаємо тотожність

. (3.5)

Ця тотожність має таку інтерпретацію: позика суми 1 може бути амортизована щорічними платежами на початку року в розмірі . Інший спосіб полягає в попередній виплаті відсотка () по позиці щорічно і величини 1 в момент 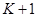: чиста річна премія для відповідного контракту страхування життя дорівнює 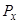. Тотожність (3.5) означає, що сукупні річні виплати є рівними в обох випадках.

Співвідношення (3.5) аналогічне іншій тотожності з теорії відсоткових ставок

, (3.6)

яке має подібну інтерпретацію.

Замінивши 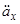на в (3.2), знаходимо

. (3.7)

Еквівалентну тотожність

(3.8)

можна розуміти таким чином: Покриття 1 можна фінансувати річними преміями 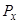; з іншої сторони, можна уявити, що ми позичили величину для оплати чистої одиничної премії. Відсоток по позиці виплачується щорічно на початку року, і позика віддається наприкінці року смерті; річна премія для відповідного контракту страхування життя дорівнює . Рівність (3.8) показує, що сумарні річні виплати в обох випадках однакові.

Розглянемо терміновий контракт терміном 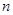років (застрахована сума 1 виплачується наприкінці року смерті). Його чиста річна премія позначається 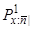. Збиток страхувальника становить

, (3.9)

або, як в (3.3)

. (3.10)

Чиста річна премія дорівнює

. (3.11)

3.2 Чисте дожиття

Нехай застрахована сума дорівнює 1 і термін дорівнює 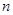. Чиста річна премія позначається через 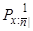. Збиток страхувальника дорівнює

. (3.12)

Чиста річна премія, очевидно, дорівнює

. (3.13)

3.3 Дожиття

Чиста річна премія позначається через 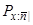. Рівності

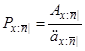(3.14)

і

(3.15)

очевидні. Збиток страхувальника дорівнює сумі (3.9) і (3.12).

По аналогії з (3.5) і (3.8) ми маємо

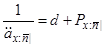, (3.16)

, (3.17)

з відповідною інтерпретацією. Рівняння (3.17) можна також отримати додаванням співвідношень

, (3.18)

, (3.19)

кожне з яких має інтерпретацію, яка аналогічна (3.8).

3.3 Відкладені аннуітети життя

Чиста річна премія, яка виплачується протягом виплачуваного протягом обраного періоду для аннуітету життя суми 1, що починається в момент 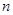, дорівнює .

Дата добавления: 2014-01-04