Рекурентні формули

Повернемося до загального контракту страхування життя, введеному в розділі 5 теми 5. Резерв чистої премії наприкінці року 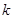за означенням дорівнює

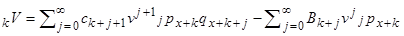. (3.1)

Для отримання зв’язку між 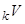і підставимо

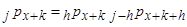(3.2)

у всі, крім перших 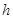, доданки в (3.1), і замінимо індекс сумування на 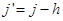. В результаті співвідношення, яке поєднує 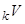і , має вид

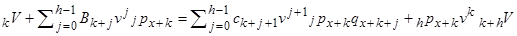. (3.3)

Це співвідношення має таку інтерпретацію: Якщо застрахований живий наприкінці року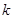, то резерв чистої премії, разом з очікуваним поточним значенням премій, підлягає виплаті протягом наступних 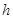років, дорівнює сумі, яка необхідна застрахованому для купівлі страхування життя в цей період, плюс вартість контракту на чисте дожиття наприкінці року .

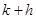Рекурентне рівняння для резерву чистої премії отримується при :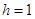

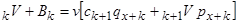. (3.4)

Таким чином, резерв чистої премії можна обчислити рекурентним чином в двох напрямах: 1) Можна обчислити послідовно 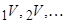в цій послідовності, починаючи зі значення 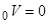; 2) Якщо контракт має скінчену тривалість 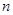, то можна обчислити 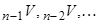в цій послідовності, починаючи з відомого значення 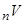. Наприклад, в числовому прикладі розділу 2 ми маємо 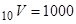для контракту на дожиття і 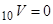для термінового страхування.

Рівняння (3.4) показує, що сума резерву чистої премії в момент 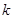і премії дорівнює очікуваному поточному значенню фонду, що необхідний наприкінці року (він дорівнює 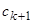у випадку смерті, інакше - ). Інша інтерпретація можлива, якщо записати

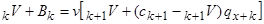. (3.5)

Величина необхідна в будь-якому випадку. Додаткова величина, яка необхідна у випадку смерті, є чистою ризиковою величиною.

Рівняння (3.5) показує, що премію можна розділити на дві компоненти, 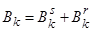, де

(3.6)

є премія збережень, що використовується для збільшення резерву чистої премії, і

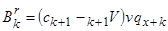(3.7)

є премія за терміновим однорічним контрактом для покриття чистої ризикової величини, або ризикова премія. Тому операцію в рік 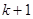можна інтерпретувати як комбінацію операції чистого збереження і термінового однорічного контракту. Ми припускаємо, що застрахований живий в момент .

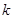Помноживши (3.6) на 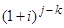и сумуючи по 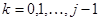, отримаємо

, (3.8)

тобто резерв чистої премії дорівнює накопиченому значенню премій збережень, виплачених від початку контракту.

Розподіл на премію збережень і ризикову премію в числовому прикладі розділу 2 наведено в таблиці

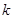
	Контракт на дожиття	Контракт на дожиття	Терміновий контракт	Терміновий контракт
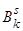
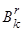
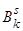
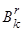
	74.17	14.79	1.22	16.00
	75.24	13.71	0.97	16.26
	76.43	12.53	0.70	16.53
	77.74	11.22	0.42	16.81
	79.18	9.78	0.12	17.10
	80.77	8.18	-0.19	17.41
	82.53	6.43	-0.52	17.74
	84.47	4.49	-0.87	18.09
	86.60	2.36	-1.24	18.46
	88.96	0.00	-1.62	18.85

Записуючи (3.5) в формі

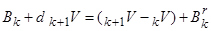, (3.9)

ми бачимо, що премія плюс відсоток, отриманий від резерву чистої премії, йдуть на зміну (збільшення або зменшення) резерву чистої премії і на забезпечення ризикової премії. Це рівняння є узагальненням співвідношення (6.7) теми 3.

Помноживши (3.5) на 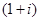, ми отримаємо рівняння, аналогічне рівності (3.9):

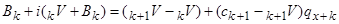. (3.10)

Рівняння (3.9) і (3.10) відрізняються тим, що в (3.9) оцінка проводиться в момент 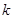, а в (3.10) – в момент .

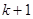Дата добавления: 2014-01-04