Неперервна модель

Розглянемо неперервну модель загального контракту страхування розділу 3. Контракт тепер визначається двома функціями (страховою сумою 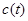і рівнем премії 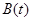в момент 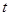, 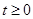). Резерв чистої премії в момент 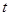дорівнює

. (11.1)

Премії можна розділити на компоненту збережень

, (11.2)

і ризикову компоненту

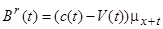. (11.3)

Тоді величина 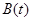,яка дорівнює сумі цих двох компонент, задовольняє диференціальне рівняння Тіле:

, (11.4)

яке є неперервною версією (3.9), (3.10), що має аналогічну інтерпретацію.

В частинному випадку

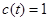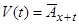, , , (11.5)

рівняння (11.4) приводить до (6.11) теми 3. Якщо

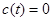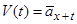, , , (11.6)

то рівняння (11.4) узгоджується з (6.6) теми 4.

Робота з неперервною моделлю спрощує викладки. Наприклад, існує тільки один метод аналізу технічного прибутку, замість двох, як в дискретній моделі розділів 9 і 10.

Припустимо, що застрахований живий в момент 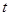, і що дійсна сила відсотка в момент 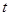дорівнює 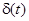. Технічний прибуток на нескінченно малому інтервалі часу від 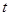до 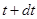, яку ми позначимо через 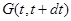, можна розкласти на

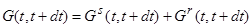, (11.7)

де

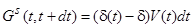(11.8)

є прибутком інвестицій, і

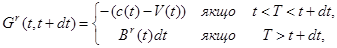(11.9)

є прибутком смертності. Зауважимо, що ймовірність смерті дорівнює 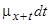і ймовірність виживання дорівнює 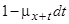, тому очікуване значення 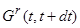дорівнює нулю. Крім цього

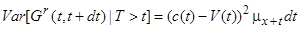, (11.10)

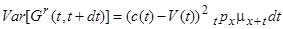, (11.11)

і

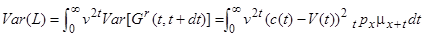, (11.12)

по аналогії з (7.7) і (7.10).

Використовуючи контракт страхування життя в якості прикладу, ми покажемо як прибуток інвестицій можна використати для неперервного збільшення виплат. Припустимо, що укладено контракт неперервного аннуїтету зі сталою інтенсивністю платежу 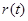в момент 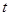. Резерв чистої премії в момент 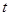дорівнює

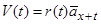. (11.13)

В момент 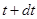рівень виплат виростає до 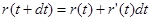за рахунок прибутку інвестицій. Це приводить до умови

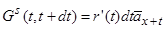. (11.14)

Використовуючи (11.8) і (11.13), отримуємо диференціальне рівняння для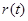

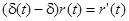, (11.15)

яке має розв’язок

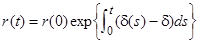, (11.16)

який узгоджується з результатом, що отриманий наприкінці розділу 10.

Ми бачили в цьому і попередніх двох розділах як прибуток інвестицій може збільшити виплати на основі еквівалентності. З іншої сторони, неможливо передати прибуток смертності: смерть застрахованого приносить збиток від смертності (у випадку контракту страхування життя) чи прибуток смертності (у випадку аннуїтета), що неможливо передати застрахованому.

Однак, можливо передати прибуток (або збиток) смертності групі застрахованих. Розглянемо групу, яка складається з 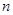людей; всі мають однаковий початковий вік 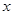і підписані контракти зі страховою сумою 1. Встановлено угодою, що довільний прибуток смертності (або збиток) передається застрахованим в формі збільшених (зменшених) майбутніх платежів. Визначимо, що буде значенням 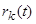, ставки аннуїтета в момент 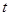, якщо з часом тільки 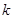від початкових 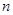людей продовжують жити.

Припустимо, що 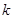осіб є живими в момент 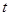і що всі виживають в момент 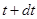, прибуток смертності буде від’ємним; з розрахунку на одну особу, яка продовжує жити це складає

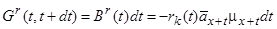, (11.17)

див. (11.9). Зменшення річної ставки випливає з умови

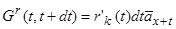, (11.18)

звідки в свою чергу маємо диференціальне рівняння

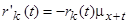. (11.19)

Якщо одна з 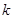осіб помирає в момент 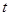, виникає миттєвий прибуток смертності 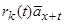; він буде розподілений між 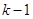особами, які вижили, для збільшення річної ставки. Нові річні ставки отримуються умови, що резерв чистої премії не повинен змінитися

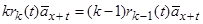. (11.20)

Звідси отримуємо

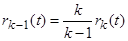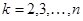, . (11.21)

Явний розв’язок знаходиться з використанням (11.19), (11.21) при початковій умові 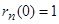і дорівнює

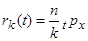, . (11.22)

Таке перетворення можна проводити, поки жива хоча б одна особа. В цьому випадку прибуток дорівнює

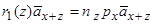, (11.23)

де 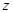означає час смерті останньої особи.

Дата добавления: 2014-01-04