Відносний рух точки. Сили інерції

Контрольні запитання

1. Яка фізична величина є мірою інертності тіла?

2. Якою фізичною величиною характеризується зміна стану спокою або руху тіла зі сталою швидкістю.

3. Сформулюйте закони Ньютона.

4. Що таке рівняння руху точки? Запишіть диференціальне рівняння руху матеріальної точки.

5. Сформулюйте першу задачу динаміки. Як вона розв’язується коли рівняння руху матеріальної точки задано векторним (координатним) способом?

6..Сформулюйте обернену (другу) задачу динаміки. Як вона розв’язується?

7. Що додатково потрібно знати для однозначного розв’язання другої (оберної) задачі динаміки?

Виберемо інерціальну систему координат () і назвемо її абсолютною (рис. 2.1). В цій системі другий закон Ньютона виконується і має вид

, (2.1)

де - прискорення точки відносно інерціальної системи (абсолютне прискорення), - результуюча сила, яка діє на точку М.

Нехай система координат (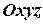) рухається відносно даної інерціальної () (рис. 2.1) за відомим законом. В рухомій системі координат матеріальна точка 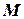рухається з відносним прискоренням . Прискорення точки в абсолютній та рухомій системі зв’язані теоремою про складання прискорень для складного руху

, (2.2)

де – прискорення переносного руху точки, - прискорення Коріоліса.

Підставляючи рівняння (2.2) в (2.1) отримуємо

. (2.3)

Перепишемо рівняння (2.3) для спостерігача, що знаходиться в рухомій (неінерціальній) системі, у такому вигляді, щоб воно мало такий самий вигляд, як і в інерціальній

, (2.4)

де

. (2.5)

Рівняння (2.4) описує відносний рух точки. Таким чином, для опису руху в рухомій системі до результуючої зовнішніх сил треба додавати „силу інерції” (дивись рис. 2.2), яка може мати дві складові

, (2.6)

так звана переносна сила інерції, та

, (2.7)

сила інерції Коріоліса.

Отже, сили інерції обумовлюють різницю між відносним і абсолютним прискореннями і вибирають їх такими, щоб вони забезпечували в неінерціальній системі відліку ті прискорення, які фактично мають місце для спостерігача, який знаходиться в цій неінерціальній системі.

Нагадаємо що, в загальному випадку прискорення переносного руху може складатися з трьох доданків

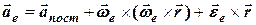, (2.8)

які зумовлені поступальним рухом неінерціальної системи та обертальним рухом цієї системи (доданки та ).

Сили інерції залежать від:

1. Властивостей неінерціальної системи - від прискорення поступального руху системи , її кутового прискорення 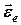та кутової швидкості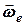

. (2.9)

Перший доданок

, (2.10)

зумовлений прискореним поступальним рухом системи – така сила виникає при гальмуванні або прискоренні судна, коли нас „відкидає” у напряму, протилежному прискоренню.

Другий доданок

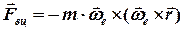, (2.11)

називають відцентровою силою, бо ця сила напрямлена вздовж радіуса обертання від осі обертання і діє на нерухому точку.

Останній доданок

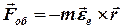, (2.12)

називається обертальною силою інерції, яка виникає при зміні кутової швидкості обертання системи - ця сила напрямлена проти тангенціального прискорення. Прояв сили нерівномірного обертання ми відчуваємо коли карусель набирає оберти або гальмує, тоді ми або притискаємося до спинки сидіння, або від неї відриваємося.

2. Від властивостей системи та тіла – якщо рухома система здійснює обертальний рух з кутовою швидкістю , а тіло в ній рухається з відносною швидкістю , то виникає сила інерції Коріоліса

. (2.13)

Дата добавления: 2014-01-04