Задачі динаміки

Розділ III. ДИНАМІКА

Контрольні запитання

1 Який рух точки називається складним?

2 Який рух називають відносним? переносним? абсолютним?

3 Який зв’язок існує між абсолютною, переносною та відносною швидкостями точки?

4 Запишіть формулу для визначення абсолютного прискорення точки при її складному русі та поясніть кожний доданок.

5 Дайте визначення прискорення Коріоліса. Від яких величин воно залежить? В яких випадках прискорення Коріоліса дорівнює нулю?

6 В яких точках Землі та як повинно рухатись судно з незмінною величиною швидкості, щоб прискорення Коріоліса: а) дорівнювало нулю?
б) мало найбільше значення?

Динаміка є частиною теоретичної механіки, в якій вивчається рух тіл як результат їх взаємодії. Основи динаміки були закладені Ньютоном, який узагальнив накопичені до нього досліди по руху тіл і сформулював три основні закони механіки.

Пряма (перша) задача динаміки – визначити рівнодійну сил , що діють на матеріальну точку, якщо відома її маса 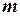та кінематичні рівняння руху.

1. Якщо закон руху матеріальної точки задано векторним способом

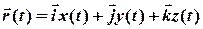, (1.1)

який еквівалентний трьом скалярним рівнянням:

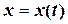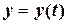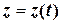, , , (1.2)

то задача розв’язується однозначно шляхом подвійного диференціювання.

Дійсно, швидкість визначиться як перша похідна закону руху за часом 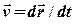, а прискорення – як друга похідна . Тоді для визначення сили за відомим значенням маси 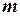точки, отримаємо

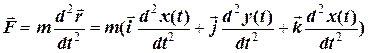. (1.3)

Останній вираз називають диференціальним рівнянням руху точки.

Друга (або обернена) задача динаміки – визначити рівняння руху вільної матеріальної точки, якщо задана її маса 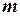, прикладена сила та відомі початкові умови.

Для визначення закону руху 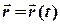необхідно розв’язати диференціальне рівняння другого порядку виду

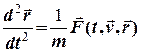, (1.4)

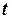бо в загальному випадку сила залежить від часу , положення точки 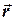та її швидкості 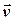. Диференціальне рівняння (2.1) у векторній формі еквівалентне трьом скалярним рівнянням. В залежності від вибору системи координат можна отримати різні форми скалярних диференціальних рівнянь руху матеріальної точки.

Розв’язок рівняння (2.1) можна отримати користуючись загальними методами розв’язання диференціальних рівнянь, а в ряді випадків шляхом двох послідовних інтегрувань. Загальний розв’язок рівняння (2.1) буде мати вигляд

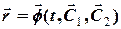. (1.5)

Щоб довести розв’язок задачі до кінця, потрібно визначити значення сталих векторів 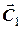та 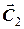. Тому рівняння (2.1) необхідно доповнити двома умовами, які фіксують стан точки в певний момент часу. Як правило, вказують значення радіус-вектора та швидкості точки в початковий момент часу 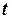= 0:

, (1.6)

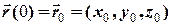, (1.7)

які називають початковими умовами.

Отже, однозначний розв’язок оберненої (другої) задачі динаміки для вільної матеріальної точки масою 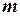може бути знайдений, якщо відомий закон сили та задані початкові умови (1.6 – 1.7).

Дата добавления: 2014-01-04