Як коливання фізичного маятника

Фізичний маятник – це будь-яке тіло, що підвішене у точці, яка не співпадає з центром його маси, та має можливість здійснювати коливання навколо цієї точки.

Розглянемо таке тіло, яке підвішене в точці 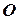та відхилене від положення рівноваги на кут 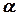(рис. 6.1). В цьому випадку сила тяжіння , яка прикладена до центру маси тіла (точка 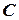), створює момент сили 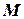відносно точки підвішування

. (6.1)

Цей момент намагається повернути тіло навколо точки підвішування до положення рівноваги (у протилежну сторону від відхилення). Таким чином, основне рівняння обертального руху може бути записано у вигляді

, (6.2)

де – момент інерції тіла відносно точки підвішування.

Отримали нелінійне диференціальне рівняння, розв’язок якого є окремою математичною задачею. Проте для малих кутів відхилення рівняння (6.2) стає лінійним і зводиться до відомого рівняння гармонічних коливань

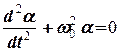, (6.3)

в якому

, (6.4)

- частота коливань, з якою зв’язаний період коливань

. (6.5)

В останній формулі

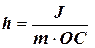(6.6)

– так звана зведена довжина фізичного маятника. Остання дорівнює довжині математичного маятника з тим самим періодом коливань.

Таким чином, щоб знайти період (чи частоту) малих коливань фізичного маятника, треба знати масу тіла 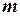, відстань 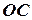між точкою підвішування та центром маси тіла і момент інерції тіла відносно точки закріплення.

Розглянемо коливання судна, як коливання фізичного маятника. Як зазначено в попередньому параграфі судно можна нахиляти як в поперечній, так і в продольній площинах (рис.5.1 та 5.2), тому існує 2 головних метацентра: поперечний 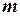(який відіграє основну роль в бортових коливаннях судна) та поздовжній метацентр 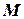(який відіграє основну роль в кільових коливаннях судна).

Тоді, наприклад, для бортових коливань судна малої амплітуду маємо наступне рівняння

, (4.1)

де – - моменти інерції судна відносно поздовжньої осі, що проходять через його центр ваги та – висота поперечного метацентра над центром ваги (рис.5.1). Розв’язок цього рівняння має вид:

, (4.2)

де частота коливань

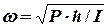, (4.3)

або період бортових коливань

, (4.4)

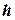Формула, аналогічна до (4.1), буде і для кільових коливань, лише з заміною моменту інерції на – момент інерції судна відносно поперечної осі, що проходять через його центр ваги, та висоти поперечного метацентру на 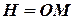- висоту поздовжнього метацентру над центром ваги (рис.5.2). Тому для кільових коливань судна отримуємо наступне рівняння:

(4.5)

Звідки для періоду кільових коливань судна маємо

. (4.6)

Звернемо увагу, що на практиці визначають період власних бортових коливань судна на тихій воді шляхом запису загасаючих коливань. Знаючи період цих коливань , розраховують метацентричну висоту 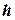за допомогою “капітанської” формули:

, (4.7)

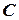де та 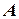– розмірні коефіцієнти, 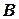- ширина судна, - розподіл ваги відносно вертикальної площини симетрії. Отже величина 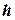залежить від розподілу ваги по судну, чим більше вантажів біля центру, тим менше значення , а якщо вантажі біля бортів, то 1.

Зауважимо, що ця емпірична „капітанська” формула є наслідком отриманого виразу для періоду бортових коливань (4.3). З цієї формули отримуємо:

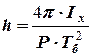(4.8)

Оскільки момент інерції судна відносно поздовжньої осі, що проходять через його центр ваги, пропорціональний вазі судна та квадрата його поперечного розміру, тобто

, (4.9)

тоді з рівняння (4.6) отримуємо:

(4.10)

що співпадає з „капітанською” формулою (4.5) та дозволяє з’ясувати значення коефіцієнта .

Якщо врахувати силу опору лінійну по кутовій швидкості, то отримаємо наступне диференціальне рівняння бортових коливань:

, (4.11)

розв’язок якого має вид:

, (4.12)

тут , , а 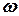визначається формулою (4.3). Отже, сили опору зумовлюють загасання коливань та викликають зменшення частоти коливань.

В реальній ситуації хитавицю судна викликає дія хвиль, які змінюються за гармонічним законом:

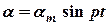, (4.13)

Що викликає діє моменту сили, що змінюється за таким самим законом

. (4.14)

Тоді в наближенні, що ширина судна значно менша, ніж довжина хвилі отримуємо:

(4.15)

Розв’язок цього рівняння для бортових вимушених коливань дає відомий результат

(4.16)

- коли кожному значенню відповідає певне значення амплітуди 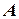вимушених лінійних коливань, яка залежить від частоти

, (4.17)

а графік залежності амплітуди вимущених коливань від частоти збуджуючої сили зображений на рис.6.2.

Дата добавления: 2014-01-04