Диференційне рівняння теплопровідності

Розглянуті раніше питання пов’язані зі стаціонарним температурним полем. Але на практиці інженеру доводиться займатись розв’язанням проблем, де в об’єктах відбуваються процеси переносу теплоти, коли температурне поле залежить як від координат, так і часу, тобто має місце нестаціонарне температурне поле. У цьому випадку необхідне розв’язання диференційного рівняння теплопровідності. Якраз це рівняння дає залежність між температурою, часом та координатами.

Виконаємо виведення диференційного рівняння теплопровідності.

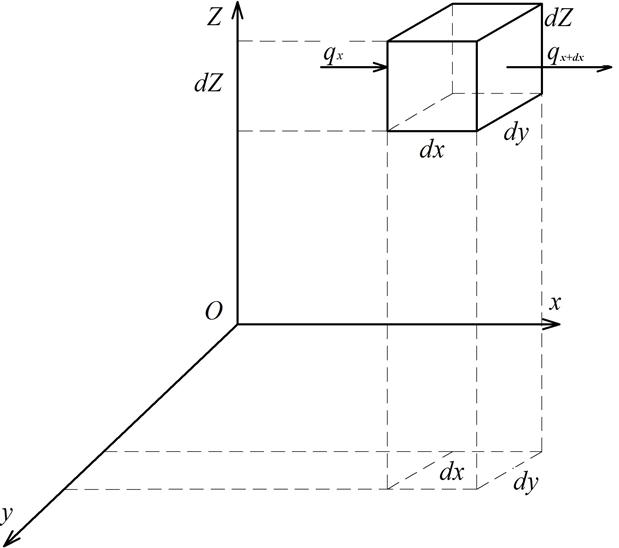
Рисунок 1.5. До виведення рівняння теплопровідності

Виділимо в однорідному середовищі елементарний об’єм у формі паралелепіпеда з ребрами dx, dy, dz. Через ліву грань об’єму проходить питомий тепловий потік q_x, а через праву – q_x+dx. Припустимо, що q_x>q_x+dx. Це означає, що відбувається нагрів об’єкта. Вважаємо, що градієнт питомого теплового потоку дорівнює 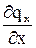. Повний приріст питомого теплового потоку на відстані dx становить dx. Відповідно по осям x,y,z через протилежні грані будуть виходити такі питомі теплові потоки:

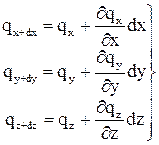(1.36)

Маємо по осям x, y,z грані паралелепіпеда з такими площами: dydz, dxdz, dxdy. Тоді кількість теплоти, що проходить через ліву грань по осі х за час 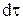становить q_xdydzd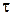, а через праву – q_x+dxdydzd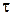. Оскільки відбувається нагрів елемента, то різниця між кількостями теплоти, що входить в об’єкт і виходить із нього представляє собою теплоту, акумульовану елементарним об’ємом.

(1.37)

тобто

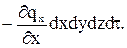
По всім осям отримуємо загальний приріст теплоти

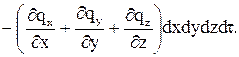(1.38)

Ця величина представляє собою всю теплоту, акумульовану за час d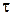елементарним об’ємом dxdydz. Вона може бути представлена як добуток маса Х питома теплоємкість Х приріст температури. Приріст температури за одиницю часу дорівнює , а за час d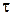становить . Тоді будемо мати

де 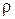- густина,

- маса елементарного об’єму;

с – питома теплоємкість,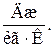

Після скорочення отримаємо

(1.39)

Застосовуючи закон Фур^,є для теплопровідності

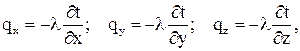
знаходимо

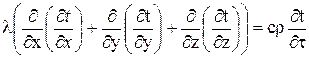. (1.40)

Вираз називається оператором Лапласа і позначається 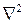. Тоді диференційне рівняння теплопровідності має такий вигляд

(1.41)

Якщо фізичні величини 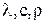не залежать від температури, то комплекс позначається латинською буквою, а і називається коефіцієнтом температуропровідності. Цей коефіцієнт характеризує теплоінерційні властивості речовини. Чим більше значення має цей коефіцієнт, тим швидше розповсюджується теплота усередині об’єкта.

Диференційне рівняння (1.39) має безліч розв’язків. для отримання його однозначного розв^,язку необхідно використати додаткові, так звані крайові умови. Існують два види крайових умов:

- початкові, що характеризують розподіл температури в тілі в який-небудь початковий момент часу (наприклад, );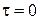

- граничні умови, що показують теплові особливості на поверхні речовини.

Існують чотири способи завдання граничних умов:

- граничні умови 1-го роду: задана відома функція температури від часу для поверхні об’єкта;

- II-го роду: задана функція зміни теплового потоку через поверхню тіла, що знаходиться в процесі теплообміну;

- III-го роду: задано закон теплообміну між поверхнею тіла та навколишнім середовищем;

- IV-го роду: мається контактний теплообмін між поверхнями двох щільно контактуючих об’єктів.

ГЛАВА 2

Дата добавления: 2014-01-04