Важiльнi механiзми

а) - кривошипно-коромисловий; б) - кривошипно-повзунний в) - кулiсний

Рис. 1.5.

Кулачкові механізми

а ) -з коромисловим штовхачем б) – з роликовим штовхачем

в) – з тарiлчастим штовхачем

Рис.1.6.

Фрикцiйний механiзм Зубчастий механiзм

Рис 1.7. Рис 1.8.

Механiзм з гнучкою ланкою

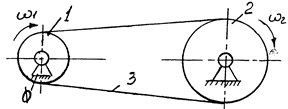Рис. 1.9.

1.4. Компоненти механізму.

Всякий механізм чи машина, якими складними вони не були б, складаються із окремих деталей (компонентів, елементів).

Виріб, виготовлений із однорідного матеріалу, без застосування складальних операцій, називається деталлю (вал, зубчасте колесо, болт). Деталі між собою з'єднуються рухомо, або нерухомо (жорстко).

Деталь (компонент), або жорстке з'єднання декількох деталей, що несе елементи кінематичних пар, називається ланкою.

Місце рухомого з'єднання двох ланок називається кінематичною парою.

Ланки мають різноманітне конструктивне оформлення залежно від призначення і технологічних умов (рис, 1.5).

Всякий механізм має нерухому ланку, або ланку, що приймається за нерухому, яка називається стояком (0 — рис. 1.5).

Із рухомих ланок виділяють вхідні і вихідні (ведучі та ведені).

Вхідною ланкою (ведучою) називається ланка, закон руху і сили якій задається (1 - рис.1.5).

Вихідною (веденою) називається ланка, від якої отримуються потрібні рухи і сили для робочого органу механізму (3 — рис. 1.5).

Останні ланки називаються з'єднувальними, або проміжними. В більшості випадків в механізмах одна вхідна і одна вихідна ланка. Вхідна ланка отримує рух від двигуна, а вихідна з'єднується з робочим органом машини.

Залежно від характеру руху відносно стояка інші ланки називають:

Кривошипом - обертову ланку, яка може здійснювати повний оберт навколо нерухомої осі (1 – рис. 1.5);

Шатуном - ланку, що з'єднана обертальними кінематичними парами тільки з рухомими ланками (2 - рис.1.5, а, б);

Повзуном - ланку, яка утворює поступальну пару з однією ланкою і обертальну з другою (3 – рис. 1.5, б);

Коромислом - обертову ланку, що здійснює неповний оберт навколо нерухомої осі (3 – рис. 1.5, а);

Кулісою - обертову ланку, яка є напрямною повзуна (3 – рис. 1.5, в);

Ковзаючим каменем - ланку, що здійснює прямолінійно - поступальний рух вздовж рухомої напрямної (2 — рис. 1.5, в);

Напрямною - ланку, що обмежує рух ковзаючого каменю (3 - рис. 1.5, в), або повзуна (0 - рис. 1.5, б);

1.5. Кінематичні пари та їхня класифікація.

Місце рухомого з'єднання двох ланок називається кінематичною парою. За характером стикання поверхонь кінематичні пари діляться на вищі і нижчі.

До нижчих пар відносяться пари, у яких стикання елементів про­ходить по поверхням /поршень з циліндром/.

До вищих пар відносяться пари, у яких стикання елементів проходить по лініям або точкам /колесо з рейкою/.

Способи з'єднання ланок в кінематичні пари, тобто сполучення елементів кінематичних пар бувають різноманітні. Теорію кінематич­них пар розробив вчений Х.І.Гохман /1890р./. Ця теорія була вдос­коналена вченими А.П.Малишевим, В.В. Добровольським і І.І.Артоболевським. Коротко її суть в наступному.

На відносний рух кожної ланки кінематичної пари накладаються певні обмеження, які залежать від способу з'єднання ланок пари.

Обмеження, накладені на відносний рух ланок кінематичної пари, називаються умовами зв'язку.

Розглянемо, які ж зв'язки і в якій кількості можуть бути накла­дені на відносний рух ланок кінематичної пари.

В загальному випадку всяке абсолютно тверде тіло, що вільно, ру­хається в просторі, має шість незалежних переміщень, тобто має шість ступенів вільності

З’єднання однієї ланки рухомо з іншою ланкою, тобто утворення кінематичної пари накладає на відносний рух цих ланок обмеження, тобто умови зв'язку. Число умов зв'язку, очевидно, повинно бути ці­лим і меншим шести. Якщо число умов зв'язку дорівнює 6, ланки втрача­ють відносний рух і переходять в жорстке з'єднання. Якщо число умов зв'язку дорівнює нулю, то ланки не дотикаються і отже не утворюють кінематичної пари. Таким чином, число умов зв'язку змінюється від І до 5.

Число ступенів вільності Н ланки кінематичної пари з числом умов зв'язку S можна зв'язати виразом

Н = 6 - S. /1.1/

Зв'язки, накладені на відносний рух ланок кінематичної пари, обмежують ті можливі відносні рухи, які мають ланки. Всі кінематич­ні пари діляться на класи в залежності від числа умов зв'язку.

Очевидно, оскільки число умов зв'язку змінюється від І до 5, то число класів кінематичних пар дорівнює п'яти.

Клас кінематичної пари визначається числом умов, зв'язку. Із /1.1/ маємо

S = 6 - Н. /1.2/

Якщо кінематична пара має 5 ступенів вільності Н = 5, то згідно /1.2/ S = 6 -5= І; така кінематична пара відноситься до І класу.

Розглянемо найпоширеніші кінематичні пари /рис.1.10/.

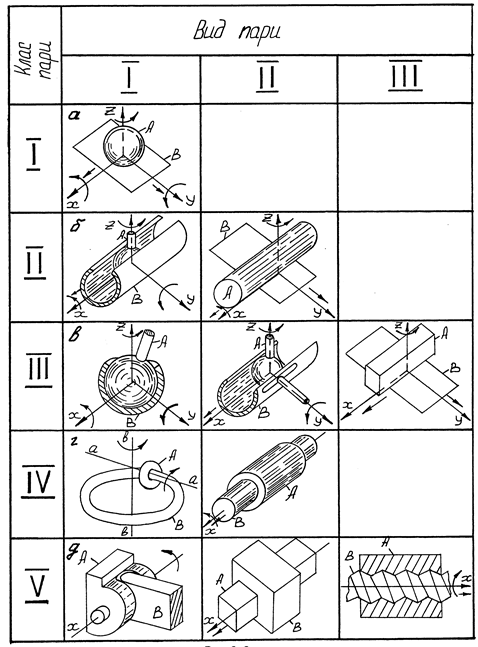
Класифікація кінематичних пар

Рис.1.10

Вид кінематичної пари визначається числом поступальних і обертальних рухів. Обертальним рухам надається перевага. Так, якщо для даного класу кінематичної пари є максимальне число обертальних ру­хів, то пара відноситься до першого виду, якщо обертальний рух замінено поступальним, то пара відноситься до другого виду і т.д.

1.6. Кінематичні ланцюги та їхня класифікація.

Сукупність ланок, з'єднаних між собою кінематичними парами, називається кінематичним ланцюгом /рис.1.11./.

Кінематичні ланцюги діляться на прості і складні.

Простим кінематичним ланцюгом називається такий ланцюг у якого кожна ланка входить не більше, чим у дві кінематичні пари /рис.1.11.а/.

Складним кінематичним ланцюгом називається такий ланцюг, у якого хоч би одна ланка входить більш як у дві кінематичні пари /рис.1.11.б/.

Прості і складні кінематичні ланцюги у свою чергу діляться на замкнуті і незамкнуті.

Незамкнутим кінематичним ланцюгом називається такий ланцюг, у якого хоч би одна ланка входить в одну кінематичну пару /рис.1.11.а/.

Замкнутим кінематичним ланцюгом називається такий ланцюг, у якого кожна ланка входить не менше, ніж у дві кінематичні пари /рис.1.11.б/.

Кінематичні ланцюги бувають плоскі і просторові.

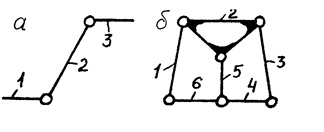Кінематичні ланцюги

а - простий незамкнутий; б - складний замкнутий

Рис.1.11

1.7. Структурні формули кінематичних ланцюгів.

Число ступенів вільності кінематичного ланцюга залежить від чис­ла ланок, з яких складається ланцюг, а також від класу та числа кінематичних пар, що входять до складу ланцюга.

Кожна ланка в просторовому русі має шість ступенів вільності. Сукупність n ланок являє собою систему з 6n ступенями вільності. Кожна кінематична пара V класу зменшує число ступенів вільності на п'ять; пара ІV класу - на чотири, Ш класу - на три і т.д.

Число ступенів вільності W просторового кінематичного ланцюга, що складається із n рухомих ланок і кінематичних пар п'ятого клаcу p₅, четвертого p₄, третього p₃, другого p₂ i першого р₁ буде:

W = 6n - 5p₅ - 4p₄ - 3p₃ - 2p₂ – p₁ . /1.3/

Це рівняння являє собою формулу рухомості, або структурну фор­мулу просторового кінематичного ланцюга і носить назву формули Сомова-Мaлишева.

У випадку плоского кінематичного ланцюга кожна ланка, будучи вільною, має три ступені вільності, а при наявності п - ланок – 3п ступенів вільності. В склад плоского кінематичного ланцюга можуть входити тільки кінематичні пари V класу /обертальні і поступальні/ і ІV класу /зубчаста передача/. Кінематична пара V класу в відносному русі однієї ланки відносно другої зменшує ступінь вільності на 2, а ІV класу - на І. Звідси ступінь вільності плоского, кінематичного ланцюга

W = 3n - 2p₅ - p₄ . /1.4/

Це рівняння носить назву формули Чебишева. Воно вперше отримано в 1869 р. Всякий механізм є частковим випадком, кінематичного ланцюга, але не кожний кінематичний ланцюг є механізмом.

1.8 Принцип утворення механізмів.

Принцип утворення механізмів був вперше сформульований Л.В.Ассуром в 1914 р.

Всякий механізм може бути утворений шляхом послідовного, приєднання до ведучої /вхідної/ ланки із стояком кінематичних ланцюгів з нульовою ступінню вільності.

Механізмом називається, замкнутий кінематичний ланцюг з однією нерухомою ланкою, у якого при заданих законах рухів вхідних ланок, всі інші ланки здійснюють доцільні, наперед задані рухи /рис.1.12/.

Ведуча /вхідна/ ланка із стояком називається механізмом І класу умовно /рис.1.13/.

Рис.1.12 Рис.1.13

Ступінь вільності механізму характеризує число ступенів вільності механізму відносно ланки, прийнятої за нерухому /стояк/.

1.9. Групи Ассура та їхня класифікація.

Кінематичний ланцюг з нульовою ступінню вільності називається групою Ассура.

В сучасному машинобудуванні і автомобілебудуванні широко застосовують плоскі механізми, ланки яких входять в кінематичні пари ІV і V класів. Розглянемо принципи їх структурної класифікації. На основі викладеного принцип утворення механізмів можна сформулювати ще так: всякий механізм може бути утворений шляхом послідовного приєднання до механізму І класу груп Ассура. На основі визначення група Ассура має нульову ступінь вільності W=0. Тоді для кожної групи Ассура і права сторона рівняння /1.4/ рівна нулю

3n - 2p₅ - p₄ = 0. /1.5/

Якщо в склад, плоского механізму входять тільки кінематичні пари V класу, то із /1.5/ маємо

p₅ =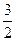n. /1.6/

Визначимо співвідношення між числом рухомих ланок і кінематичних

пар V класу в групах Ассура / рис. 1.14/ згідно / 1.6 /

Як бачимо із / 1.6 / найпростіша група Ассура складається, із двох рухомих ланок і трьох кінематичних пар V класу.

Групи Ассура діляться на класи і порядки.

Клас групи визначається найвищим класом контуру, що входить в дану групу. Клас контуру визначається числом кінематичних пар, що він в себе включає. Порядок групи визначається числом вільних елементів, якими група приєднується до основного механізму.

Дата добавления: 2014-01-04