Групи Ассура

Рис.1.14.

Групи Ассура ІІ класу ІІ порядку діляться ще на види, в залежності від наявності і співвідношення обертальних і поступальних кінематичних пар /рис.1.15/.

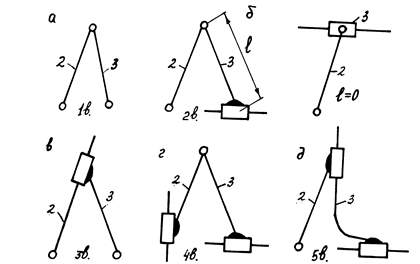Групи Ассура ІІ кл.ІІ пор.

Рис.1.15.

1.10. Класифікація механізмів. Послідовність структурного аналізу.

Якщо до механізму І класу приєднати відповідну групу Ассура:

ІІ кл. ІІ пор. І виду, то отримаємо - кривошипно-коромисловий механізм /рис.1.16,а/;

ІІ кл. ІІ пор. 2 виду - кривошипно-повзунний механізм /рис.1.16, б/;

ІІ кл. ІІ пор. 3 виду - кулісний механізм /рис.1.16, в/;

ІІ кл. ІІ пор. 4 виду - тангенсний механізм /рис.1.16, г/;

ІІ кл. ІІ пор. 5 виду - синусний механізм /рис.1.16, д/.

Клас механізму в цілому визначається найвищим класом групи Ассура, що входить в даний механізм.

Схема механізму, зображена без масштабу, називається структурною.

Схема механізму, зображена в масштабі, називається кінематичною.

Механізми, в склад яких входять тільки нижчі кінематичні пари, називаються важільними.

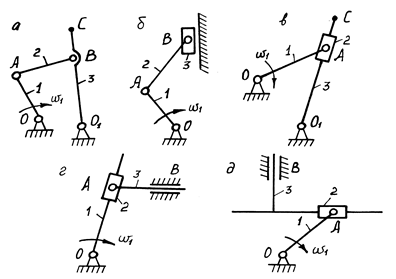Різновиди механізмів ІІ кл.ІІ пор.

Рис.1.16.

Розкладання механізму на групи Ассура проводиться в послідовності оберненій утворенню механізму, починаючи з найпростішої групи і так, щоб механізм, що залишається, був працездатним і не було розриву кінематичного ланцюга; якщо не можливо виділити найпростішу групу Ассура, то виділяємо наступну за складністю групу і т.д.

Структурний аналіз механізмів проводиться в наступній послідовності:

1/ визначають ступінь рухомості механізму за формулою Чебишева /1.4/;

2/ розкладають механізм на структурні одиниці: групи Ассура і механізм І класу в послідовності, оберненій утворений механізму;

3/ визначають клас, порядок і вид кожної групи;

4/ визначають клас механізму в цілому.

1.11. Зайві ступені вільності та пасивні умови зв'язку.

Під час дослідження структури механізмів можуть виявитися ступені вільності та умови зв'язку, що не впливають на характер руху всього механізму. Такі ступені вільності називають зайвими, а зв'язки - пасивними.

Як приклад розглянемо роботу кулачкового механізму /рис.1.17/.

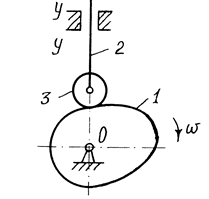Кулачковий механізм із зайвим ступенем вільності

Рис.1.17.

Кулачок І обертається навколо осі О. Штовхач 2 переміщається поступально відносно напрямних у-у. Ролик 3 може вільно обертатися навколо своєї осі, не впливаючи на характер руху всього механізму. Тобто, можливість обертання ролика є зайвим ступенем вільності. Ролик являє собою конструктивний елемент, який зменшує сили тертя і спрацювання ланок. Кінематика не зміниться, якщо ролик видалити і штовхач безпосередньо з’єднати з кулачком у кінематичну пару ІV класу.

На рис.1.18 показано механізм шарнірного чотириланковика.

Важільний механізм з пасивними зв'язками

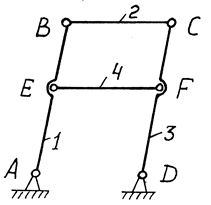Рис.1.18.

Якщо ланки 1 і 3 з'єднати ланкою ЕF з двома обертальними парами, то ступінь вільності згідно /1.4/

W = 3*4 – 2*6 – 0 = 0.

Однак, якщо ланка ЕF паралельна ланці ВС, механізм матиме один ступінь вільності, тобто W = І.

Отже, ланка EF вносить пасивні зв'язки і її можна не розглядати.

Інколи, пасивні зв’язки потрібні для забезпечення певності руху, підвищення жорсткості системи, поліпшити розподіл зусиль і ін.

Під час проведення структурного та кінематичного досліджень механізмів усі пасивні умови зв'язку та зайві ступені вільності треба з механізму попередньо вилучити, умовно видаливши відповідні ланки.

1.12. Замінюючі механізми.

Під час аналiзу плоских механізмів з вищими парами в багатьох випадках зручно умовно замінювати вищi пари нижчими.

При цьому має задовольнятися умова структурної еквівалентності, тобто, щоб замінюючий механізм мав такий самий ступінь вільності і щоб характер миттєвого відносного руху всіх його ланок не змінився.

Порядок побудови замінюючого механізму розглянемо на прикладі механізмів, зображених на рис.1.19. які мають вищу кінематичну пару.

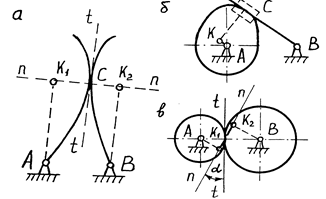Замінюючі механізми

Рис.1.19.

В точці С контакту двох ланок, які утворюють вищу кінематичну пару /рис.1.19, а/ проведемо загальну дотичну t–t до обох профілів ланок. Затим проведемо перпендикуляр до загальної дотичної в т. С, отримаємо нормаль п-п.

На лінії п - п знайдено центри кривизни профілів К₁ і К₂. В точках К₁ і К₂ ставимо обертальні кінематичні пари V класу і з’єднуємо їх допоміжними ланками з центрами А і В. Механізм АК₁К₂В і буде замінюючим. Якщо центр кривизни однієї із ланок знаходиться в нескінченності /рис.1.19, б/, то в т. С ставиться поступальна кінематична пара V класу.

Побудова замінюючого механізму для зубчастої передачі показана на рис.1.19, в.

Тема 2. Синтез важільних механізмів.

2.1. Задачі синтезу механізмів.

Проектування механізмів - це комплексна проблема, яка складається із декількох самостійних етапів. Першим етапом проектування являється розробка кінематичної схеми механізму, яка забезпечувала б необхідний вид і закон руху. Другим етапом проектування являється розробка конструктивних форм механізму, які забезпечували б його міцність, надійність, довговічність та високий коефіцієнт корисної дії і тому подібне. На третьому етапі проектування розробляються технологічні і техніко-економiчні показники механізму.

В ТММ в основному розглядаються методи за допомогою яких вирішується перший етап проектування - розробка кінематичних схем механізму, які відтворювали б необхідний закон руху. В подальшому викладі матеріалу в курсі ТММ під проектуванням механізмів ми будемо розуміти проектування їх кінематичних схем. Розділ теорії механізмів присвячений методам проектування за заданими кінематичними умовами схем механізмів, має назву синтезу механізмів.

Синтез кінематичної схеми механізму полягає у визначенні деяких постійних його параметрів /розмірів ланок, або точніше - відстаней міх осями шарнірів/, які задовольняли б деяким наперед заданим умовам /точки ланок переміщались за необхідними законами/. При цьому частина розмірів задається, а всі інші розміри повинні бути визначенні.

2.2. Синтез кривошипно повзунного механізму.

Для побудови кінематичної схеми механізму в положенні, заданому кутом φ повороту кривошипа, достатньо знати довжину кривошипа ОА /радіус r /, довжину шатуна АВ / l / і зміщення е напряму у-у руху повзуна відносно осі О обертання кривошипа. Послідовність побудови за цими даними наступна /рис. 2.1/:

1/ вибираємо довільно точку О центр обертання кривошипа;

2/ через т. О проведемо горизонтально пряму КМ;

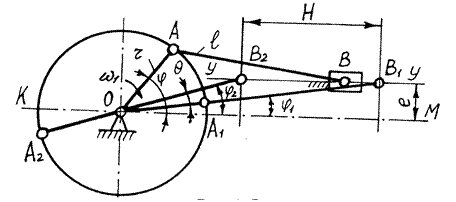Побудова кривошипно-повзунного механізму

Рис.2.1.

З/ на відстані е від прямої КМ проведемо вісь у-у, яка і буде напрямною повзуна;

4/ із центру О радіусом ОА = r опишемо траєкторію т. А;

5/ знаючи кут φ знайдемо положення кривошипа ОА;

6/ із т. А радіусом АВ = l зробимо засічку на осі у-у, отримаємо положення повзуна т. В;

7/ з’єднавши послідовно точки О, А і В, отримаємо кінематичну схему механізму.

Розглянемо найпростіші задачі синтезу кривошипно-повзунного механізму.

Введемо наступні умовні позначення:

Н - переміщення повзуна;

λ - відношення довжини шатуна l до радіуса кривошипa r,

λ = ;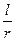

φ₁ i φ₂ - гострі кути, утворені кривошипом з напрямом ОM в крайніх положеннях повзуна;

К - коефіцієнт зміни швидкості руху повзуна, який визначається із відношення

К= 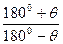, /2.1/

де 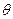= φ₂ – φ₁, тоді із /2.1/ маємо:

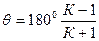. /2.2/

Задача І. Нехай відомі значення: Н, е і l.

Необхідно визначити: r і l.

Із рис.2.1 видно, що ОВ₁ = l + r і ОВ₂ = l - r. Оскiльки λ = 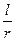, то із відношення ОВ₁ до ОВ₂ знаходимо:

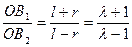. /2.3/

Розглянемо побудову трикутника ОВ₁В₂ /рис.2.2/:

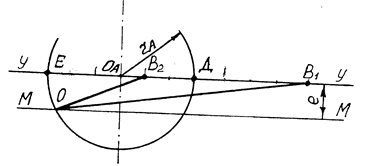Схема до визначення r і l

Рис.2.2.

І/ на довільній горизонтальній прямій у-у відкладемо відрізок В₁В₂ = Н;

2/ на відстані е від прямої у-у проведено пряму ММ;

З/ на прямій у-у знайдемо точки Д і Е так, щоб виконувалася умова:

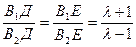; /2.4/

4/ на відрізку ДЕ, як на діаметрі, будуємо коло, /так зване коло Аполонія, радіусом r_А = ;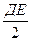

5/ на перетині кола з прямою ММ знаходимо т. О - центр обертання кривошипа;

6/ тепер із умови: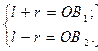

визначимо радіус кривошипа r і довжину шатуна l, для цього від першого

рівняння віднімемо друге, отримаємо:

2 r = ОВ₁ - ОВ₂ або r = 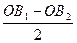, /2.5/

за тим із першого рівняння визначимо:

l = ОВ₁ – r або l = 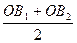. /2.6/

Задача 2. Задано: Н; λ і К.

Треба знайти: r; l і e.

Задача 3. Задано: Н; е і К.

Треба знайти: r і l.

Порядок роз'вязання задач 2 і 3 викладено в [3,4].

2.3. Синтез кривошипно-коромислового механізму.

Нехай задані довжина коромисла О₁В, відстань х між центрами О і О₁ і кути ψ₁ та ψ₂. Необхідно знайти радіус r кривошипа ОА і довжину l шатуна АВ /рис.2.3/.

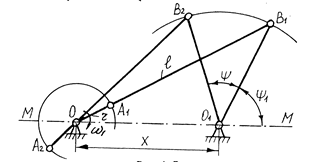Кривошипно-коромисловий механізм

Рис.2.3.

Порядок розв'язування задачі:

І/ проведемо довільну горизонтальну пряму ММ /рис.2.3/;

2/ на прямій ММ вибираємо довільно т. О - центр обертання кривошипа;

З/ на відстані х від т. О знайдемо т. О - центр обертання коромисла;

4/ із т. О₁ радіусом О₁В проведемо дугу до перетину із променями, які відкладені під кутами ψ₁ та ψ₂, отримаємо точки В₁ і В₂;

5/ з'єднаємо т. О і з точками В₁ та В₂;

6/ із умови: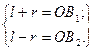

знайдемо r і l аналогічно /2.5/ і /2.6/.

2.4. Синтез кулісного механізму.

Синтез кулісного механізму розглянемо на прикладі механізму, зображеного на рис.2.4.

Задача І. Нехай задані відстань х між центрами О та О₁ та коефіцієнт нерівномірності руху К. Потрібно визначити радіус r кривошипа OA.

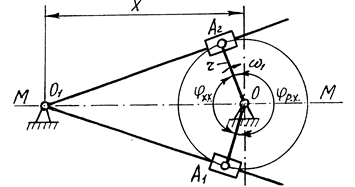Кулісний механізм

Рис.2.4.

Порядок розв’язування задачі:

І/ проведемо довільно горизонтальну пряму MM;

2 / знаючи x на прямій MM відкладемо точки О та О₁;

3/ визначимо кути холостого φ_хх і робочого φ_рх ходів із наступної умови:

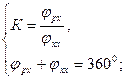/2.7/

4/ симетрично прямій ММ відкладемо кути φ_хх та φ_рх, як показано на рис.4.6;

5/ із центру О опустимо перпендикуляри на промені, які отримані в результаті відкладання кутів φ_хх та φ_рх, знайдемо точки А₁ та А₂, отже ОА₁ = ОА₂ = r.

Задача 2. Задані: коефіцієнт нерівномірності руху К і радіус кривошипа r. Визначити відстань х.

Задача 2 майже однотипна задачі І, а тому її розв'язок зрозумілий із рис.2.4.

Тема 3. Кінематичний аналіз механізмів

3.1. Основні задачі кінематичного аналізу. Функції переміщення вхідних ланок.

Основною задачею кінематичного аналізу /дослідження/ механізмів є вивчення руху ланок механізму без врахування сил, які впливають на цей рух.

Кінематичний аналіз механізмів проводиться з припущенням, що кутова швидкість вхідної ланки, при усталеному русі, постійна. Кінематичне дослідження механізмів заключається в вирішенні наступних основних задач:

а/ визначення переміщень ланок і траєкторій, що описують характерні точки ланок;

б/ визначення швидкостей окремих точок ланок і кутових швидкостей ланок;

в/ визначення прискорень окремих точок ланок і кутових прискорень ланок.

Якщо механізм має одну ступінь вільності, то переміщення, швидкості і прискорення вихідних /ведених/ ланок і будь-яких точок механізму залежать від закону руху вхідної /ведучої/ ланки. Вхідна ланка може утворювати із стояком обертальну, або поступальну кінематичну пару.

В першому випадку закон руху вхідної ланки може бути заданий у вигляді рівняння φ=φ(t), що виражає залежність кута повороту вхідної ланки від часу. В другому випадку, цей закон може бути заданий у вигляді рівняння S=S(t), що виражає залежність переміщення вхідної ланки від часу. Ці закони будемо називати функціями переміщень вхідних /ведучих/ ланок.

Функції φ=φ(t) і S=S(t) можуть бути також задані графічно у вигляді кривих, на яких по осі ординат відкладені кути повороту φ, або переміщення S в деяких вибраних масштабах, а по осі абсцис - час t у вибраному масштабі. Користуючись графіками легко визначити числові значення кутів повороту φ /рис.3.1 а/, або переміщень S за будь-який вибраний відрізок часу /рис. 3.1, б/.

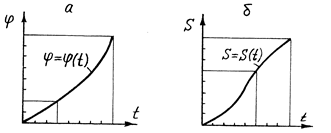Графіки переміщення вхідної ланки

а - графік кутових переміщень; б - графік лінійних переміщень

Рис.3.1.

3.2. Визначення положень ланок та траєкторій, що описують характерні точки ланок.

Щоб визначити геометричну характеристику механізмів з одним ступенем вільності, треба встановити залежності між геометричними параметрами механізму /кутами повороту його ланок, переміщеннями точок/, що змінюються в процесі руху механізму та переходу його з одного положення в інше. Це буде залежність між кутом Ψ повороту вихідної ланки механізму та кутом φ повороту вхідної ланки, тобто залежність вигляду:

Ψ = f(φ), /3.1/

для механізмів з коливальним рухом веденої ланки. Для механізмів із зворотно-поступальним прямолінійним рухом веденої ланки

S = f(φ). /3.2/

Ці залежності є функціями положення, що являють собою геометричну характеристику механізму, яка не залежить від абсолютних значень швидкостей точок ланок і визначається структурною схемою механізму та розмірами його ланок. Функції положення /3.1/ і /3.2/ навіть для найпростіших важільних механізмів виражаються складними рівняннями. Однак дістати їх у графічній формі розміткою траєкторій методом засічок значно простіше.

Для розв’язку цієї задачі повинні бути задані:

а/ кінематична схема механізму;

б/ необхідні розміри ланок;

в/ закон руху вхідної ланки.

При визначенні положень механізму викреслюється його кінематична схема в масштабі μ_l. Під масштабом розуміють число, що показує, скільки одиниць дійсної величина ланки припадає на 1 мм на кресленні

μ_l = 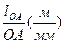, /3.3/

де l_OA - дійсна довжина ланки в м,

ОА - довжина ланки на кресленні в мм.

Побудова траєкторії точки S₂ зрозуміла з /рис.3.2/.

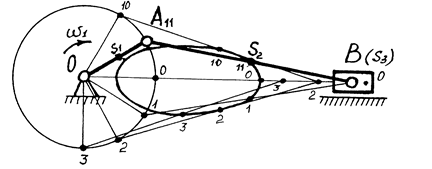Побудова траєкторії точки

Рис.3.2.

3.3. Кінематичні діаграми механізмів. Масштаби діаграм.

При кінематичному аналізі механізмів буває необхідно проводити дослідження за повний цикл руху механізму. Для цього графічне дослідження переміщень швидкостей та прискорень проводиться для ряду положень механізму. Побудуємо кінематичні діаграми, що представляють собою графічне зображення зміни одного із кінематичних параметрів ланки: переміщення, швидкості та прискорення точки ланки в функції часу, або переміщення, ведучої ланки, тобто в функції узагальненої координати.

Розглянемо побудову кінематичних діаграм на прикладі конкретного кривошипно-повзунного механізму.

Накреслимо кінематичну схему в масштабі μ_l /рис.3.3, а/. За початкове положення приймаємо те положення механізму, при якому т. В повзуна займає крайнє положення. Побудуємо механізм в дванадцяти положеннях. Для цього розділимо траєкторію точки А на кривошипі на 12 положень, починаючи з

крайнього. Методом засічок побудуємо траєкторію переміщення т. В.

Накреслимо осі координат S_B – t /рис.3.3, б/. На осі абсцис відкладаємо відрізок l в мм, що зображає час Т одного повного повороту кривошипа в масштабі μ_t. Відрізок ділимо на 12 рівних частин, і у відповідних точках по осі ординат S_B відкладаємо переміщення т. В від її крайнього положення. З'єднавши послідовно плавною кривою ці точки, отримаємо діаграму переміщення т. В в залежності від часу повороту кривошипа S_В = S_B (t).

Час Т в секундах одного повного оберту кривошипа

Т = 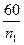= μ_t * l, /3.4/

де п₁ - частота обертання кривошипа в об/хв.

Із /5.4/ маємо масштаб часу

μ_t = 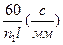. /3.5/

Масштаб переміщення точки В

μ_S = m * μ_l, /3.6/

де m = І, якщо величини переміщення т. В відкладені безпосередньо із схеми механізму; якщо переміщення т. В збільшують, або зменшують в m раз, то тоді відповідно і коефіцієнт m дорівнює числу зменшення чи збільшення переміщення т. В.

Діаграму швидкості точки В отримаємо методом графічного диференціювання діаграми переміщення точки В.

Діаграму прискорення т. В отримаємо методом графічного диференціювання діаграми швидкостей.

Після цього остаточно побудуємо повну криву прискорення точки В. Масштаби по осям ординат визначаємо за формулами:

для діаграми швидкостей μ_V = 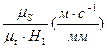; /3.7/

для діаграми прискорень μ_а = 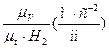, /3.8/

де Н₁ і Н₂ - відрізки в мм, взяті з креслення.

Дійсна величина швидкості та прискорення т. В в любому положенні механізму визначається шляхом вимірювання відрізків по осі ординат у відповідних положеннях механізму та перемноживши їх на відповідний масштаб:

V_B1 = 1 – 1^// * μ_V;V_B2 = 2 – 2^// * μ_V; /3.9/

а_B1 = 1 – 1^/// * μ_а;а_B2 = 2 – 2^/// * μ_а. /3.10/

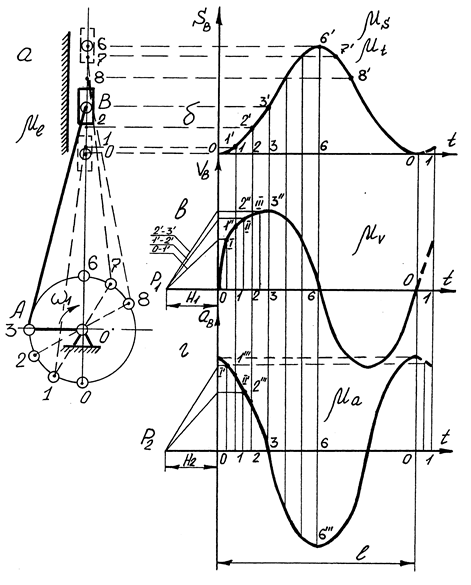Побудова кінематичних діаграм

а - кінематична схема механізму; б - діаграма переміщень т. В;

в - діаграма швидкостей; г - діаграма прискорень

Рис.3.3.

3.4. Визначення швидкостей окремих точок груп Ассура та кутових швидкостей ланок.

Розглянемо групу Ассура ІІ класу ІІ порядку першого виду, яка утворена двома ланками, що входять в три обертальні кінематичні пари /рис.3.4, а/

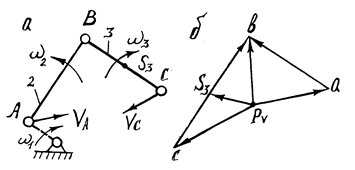Група Ассура ІІ кл., ІІ пор., І- виду.

а - кінематична схема; б - план швидкостей

Рис.3.4

Вектори швидкостей точок А і С відомі.

Знайдемо вектор швидкості точки В. Розглянемо рух точки В спочатку відносно точки А, а потім відносно точки С. Складемо векторні рівняння:

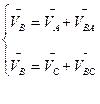/3.11/

Вектори швидкостей і 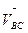руху точки В відносно точок А і С перпендикулярні відповідним ланкам АВ і СВ.

Проведемо складання векторів згідно системи рівнянь /3.11/. Для цього вибираємо, довільну точку P_V - полюс плану швидкостей /рис.3.4, б/ і з неї відкладемо вектори відомих швидкостей 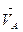і 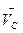. Отримаємо точки а і с. Побудову будемо вести в масштабі μ_V, який показує, скільки м/с дійсної швидкості припадає на 1 мм на кресленні.

μ_V = 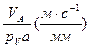. /3.12/

Далі із кінця векторів точок а і с проведемо напрями векторів перпендикулярно до ланок відповідно АВ і СВ. Місце перетину цих векторів дає точку в. З’єднаємо т. в з точкою Р_V. Відрізок Р_Vв зображає повний вектор швидкості т. В. Зв'язок між дійсними швидкостями точок і відповідними відрізками на плані швидкостей буде:

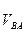= ва * μ_V;

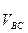= вс * μ_V; /3.13/

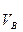= Р_Vв * μ_V...

Використовуючи план швидкостей, знайдемо кутові швидкості ланок ω₂ і ω₃:

ω₂ = 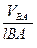; ω₃ = 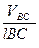. /3.14/

Для визначення напряму кутової швидкості необхідно вектор відносної швидкості перенести у відповідну точку. Стрілка вектора відносної швидкості покаже напрям обертання ланки. Так вектор в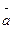 обертає ланку АВ проти годинникової стрілки, а вектор в 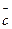обертає ланку ВС за годинниковою стрілкою.

Дата добавления: 2014-01-04