
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Визначення прискорень окремих точок груп Ассура та кутових прискорень ланок
|
|
|
|
Розглянемо групу Ассура першого виду /рис.3.5, а/.
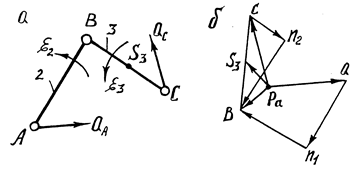 |
Група Ассура ІІ кл., ІІ пор., І виду
а - кінематична схема; б - план прискорень.
Рис.3.5.
Вважаємо, що вектори  і
і  повних прискорень точок А і С відомі.
повних прискорень точок А і С відомі.
Складемо векторні рівняння:
 /3.15/
/3.15/
де  і
і 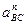 - нормальні прискорення у відносному русі;
- нормальні прискорення у відносному русі; 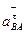 і
і  тангенціальні прискорення у тому ж русі. Знайдемо величини нормальних прискорень за відомими формулами:
тангенціальні прискорення у тому ж русі. Знайдемо величини нормальних прискорень за відомими формулами:
 =
=  ;
; 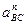 =
= 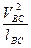 . /3.16/
. /3.16/
План прискорень /рис.3.5, б/ будуємо в масштабі μа, який показує число м/с2 дійсного прискорення, яке припадає на 1 мм креслення.
μа =  . /3.17/
. /3.17/
Вектор прискорення 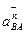 направлений паралельно ланці АВ від точки В до точки А, а вектор прискорення
направлений паралельно ланці АВ від точки В до точки А, а вектор прискорення 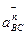 направлений паралельно ланці ВС від точки В до точки С. Вектори прискорень
направлений паралельно ланці ВС від точки В до точки С. Вектори прискорень 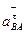 і
і  направлені перпендикулярно до відповідних нормальних. Виконаємо графічне складання векторів згідно системи рівнянь /3.15/.
направлені перпендикулярно до відповідних нормальних. Виконаємо графічне складання векторів згідно системи рівнянь /3.15/.
Дійсні прискорення точок знайдемо:
 =
=  * μа ;
* μа ;
 =
= 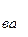 * μа ; /3.18/
* μа ; /3.18/
 =
= 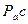 * μа .
* μа .
Знайдемо кутові прискорення ε2 і ε3 ланок АВ і ВС
ε2 = 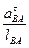 , ε3 =
, ε3 =  . /3.19/
. /3.19/
Для визначення напряму кутового прискорення необхідно вектор тангенціального прискорення перенести у відповідну точку. Стрілка вектора покаже напрям обертання ланки.
3.6. Плани швидкостей важільного механізму.
Для вирішення цієї задачі будемо вважати відомими розміри всіх ланок механізму і закон руху ведучої ланки.
Викреслимо кінематичну схему механізму /рис.3.6, а/ в масштабі μl
μl = 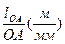 . /3.20/
. /3.20/
Побудуємо план швидкостей /рис.3.6, б/.
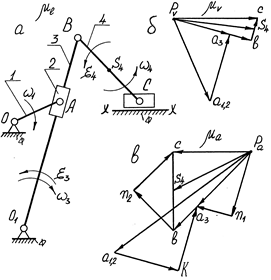 |
Механізм строгального верстату
а - кінематична схема; б - план швидкостей; в - план прискорень.
Рис.3.6.
Визначимо швидкість, т .А1.2 за величиною, що належить одночасно кривошипу І і повзуну 2
VA1.2 = ω1 * lOA. /3.21/
Вибираємо масштаб плану швидкостей
μV =  , /3.22/
, /3.22/
де pVa1.2 - відрізок на плані швидкостей в мм, що зображає повну швидкість VA1.2 в м/с. Вектор швидкості VA1.2 направлений в сторону кутової швидкості ω1, перпендикулярно до ланки ОА. Вибираємо довільну т. pV – полюс плану швид-костей і з неї відкладемо в масштабі вектор швидкості 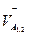 , отримаємо т. а1.2.
, отримаємо т. а1.2.
Визначимо швидкість т. А3, що належить кулісi О1В і в даний момент співпадає з т. А1.2. Розглянемо рух т. А3 відносно т. А1.2 і відносно т. О1. Складемо векторні рівняння:
 /3.23/
/3.23/
Із т. а1.2 проведемо пряму в напрямі вектору швидкості  , тобто паралельно ланці ВО, а із т. pV - пряму в напрямі вектору швидкості
, тобто паралельно ланці ВО, а із т. pV - пряму в напрямі вектору швидкості 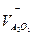 , тобто перпендикулярно ланці ВО1. Місце перетину цих прямих дає т. а3. З'єднавши т. а3 з полюсом pV отримаємо вектор
, тобто перпендикулярно ланці ВО1. Місце перетину цих прямих дає т. а3. З'єднавши т. а3 з полюсом pV отримаємо вектор  повного прискорення т. А3. Визначимо відрізок pVв, що зображає швидкість т. В, використавши відношення
повного прискорення т. А3. Визначимо відрізок pVв, що зображає швидкість т. В, використавши відношення
pVв = pVа3  /3.24/
/3.24/
Точка в лежить на продовженні відрізка pVа3.
Визначимо швидкість т. С.
Складемо векторні рівняння:
 /3.25/
/3.25/
Із т. О проведемо пряму в напрямі вектору швидкості  , тобто перпендикулярно ланці ВС, а із pV - пряму, паралельно напрямним х – х. Місце перетину цих прямих дає т. С. Вектор pVС показує повну швидкість т. С. Визначимо повну швидкість т. S4, для цього знайдемо відрізок вS4.
, тобто перпендикулярно ланці ВС, а із pV - пряму, паралельно напрямним х – х. Місце перетину цих прямих дає т. С. Вектор pVС показує повну швидкість т. С. Визначимо повну швидкість т. S4, для цього знайдемо відрізок вS4.
вS4 = вс  . /3.26/
. /3.26/
З'єднавши т. S4 з полюсом pV, отримаємо вектор швидкості т. S4.
Визначимо дійсні швидкості всіх точок
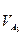 = pVа3* μV;
= pVа3* μV; 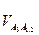 = а3а1.2* μV;
= а3а1.2* μV;  = pVс* μV. / 3.27/
= pVс* μV. / 3.27/
Визначимо кутові швидкості всіх ланок за величиною:
ω3 =  ; ω4 =
; ω4 = 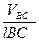 . /3.28/
. /3.28/
Для визначення напряму кутових швидкостей ω3 і ω4 перенесемо вектори лінійних швидкостей  і
і  в т. В.
в т. В.
3.7. Плани прискорень важільного механізму.
План прискорень механізму /рис.3.6, в/ будується у такій послідовності, як і план швидкостей.
Визначимо прискорення т. А1.2 за величиною. Оскільки ω1 величина стала, то повне прискорення т. А1.2 рівне нормальному прискоренню, яке визначається:
аА1.2 = . /3.29/
. /3.29/
Вибираємо масштаб плану прискорень
μа =  , /3.30/
, /3.30/
де pаа1.2 - відрізок на плані прискорень в мм, що зображає прискорення аА1.2 в м/с2. Вектор прискорень аА1.2 направлений паралельно кривошипу ОА до центру обертання, тобто від т. А1.2 до т. О.
Вибираємо довільну т. ра - полюс плану прискорень із неї відкладемо в масштабі вектор прискорення аА1.2, отримаємо т. а1.2 .
Визначимо прискорення т. А3. Складемо векторні рівняння:
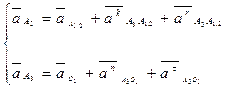 /3.31/
/3.31/
Визначимо прискорення Коріоліса і нормальне прискорення:
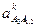 = 2ω3
= 2ω3  ;
;  =
=  . /3.32/
. /3.32/
Напрям прискорення Коріоліса збігається з напрямом, повернутого на 900 в бік кутової швидкості ω3 вектора швидкості  . Напрям відносного прискорення паралельний ланці BO1.
. Напрям відносного прискорення паралельний ланці BO1.
Із т. а1.2 відкладемо вектор прискорення Коріоліса, отримаємо т. К, через т.К проведемо пряму в напрямі відносного прискорення, тобто паралельно
ланці ВО. Із т. ра відкладемо вектор нормального прискорення, який направлений паралельно ланці BO1 і в сторону від т. А3 до т. О1 отримаємо т. п1. Через т. п1 проведемо пряму в напрямі тангенціального прискорення  , тобто перпендикулярно ланці BO1. Місце перетину цих прямих позначимо т. а3. З’єднаємо т. а3 із полюсом т. ра. Відрізок раа3 зображає вектор повного прискорення т. А3.
, тобто перпендикулярно ланці BO1. Місце перетину цих прямих позначимо т. а3. З’єднаємо т. а3 із полюсом т. ра. Відрізок раа3 зображає вектор повного прискорення т. А3.
Визначимо відрізок Рав, що зображає прискорення т. В, використавши відношення
рав = раа3 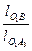 . /3.33/
. /3.33/
Точка в лежить на продовженні відрізка раа3.
Визначимо прискорення т. С.
Складемо векторні рівняння:
 /3.34/
/3.34/
Нормальне прискорення визначається аналогічно /3.32/.
Визначимо дійсні прискорення всіх точок.
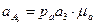 ;
;  ;
;  . /3.35/
. /3.35/
Визначимо кутові прискорення всіх ланок за величиною.
ε3 =  ; ε4 =
; ε4 =  . /3.36/
. /3.36/
Для визначення напряму кутових прискорень ε3 і ε4 перенесемо вектори тангенціальних прискорень 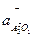 і
і  , відповідно у точки А і С.
, відповідно у точки А і С.
Змістовий модуль 2. Аналіз та синтез механізмів передач
Тема 4. Кулачкові механізми
Механізм, в склад якого входить кулачок, називається кулачковим механізмом. Кулачком називається ланка, яка має змінну кривизну поверхні і надає переміщення штовхачу. Штовхач – це ланка, яка отримує рух безпосередньо від кулачка.
 |
Кулачковий механізм
Рис.4.1
Найпростіший кулачковий механізм /рис.4.1/ складається із трьох ланок: кулачка 1, штовхача 2 і стояка 0.
Кулачкові механізми призначаються для перетворення будь – якого /безперервного/ руху ведучої ланки /кулачка/ в зворотно-поступальний або коливальний рух веденої ланки /штовхача/.
В деяких конструкціях кулачкових механізмів між кулачком і штовхачем розміщують проміжну ланку – ролик 3, який вільно обертається навколо осі, закріпленій на штовхачі. Цим досягається заміна тертя ковзання, тертям кочення, що значно зменшує знос поверхонь, як кулачка так і штовхача. Однак ролик ускладнює конструкцію кулачкового механізму.
Кулачкові механізми діляться на плоскі і просторові.
За характером руху штовхача кулачкові механізми діляться на:
1/ кулачкові механізми з обертальним рухом кулачка і поступальним рухом штовхача /рис.4.2,а/;
2/ кулачкові механізми з обертальним рухом кулачка і обертальним рухом штовхача /рис.4.2,б/;
3/ кулачкові механізми з поступальним рухом кулачка і поступальним
/обертальним/ рухом штовхача /рис.4.1,б/.
Конструкції штовхачів кулачкових механізмів діляться на:
1/ голкові /точкові/, /рис.4.3,а/;
2/ роликові /рис.4.3,б/;
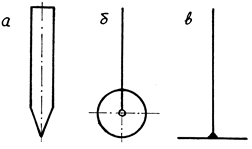 |
3/ тарілчасті /плоскі/, /рис.4.3,в/.
 |
Кулачкові механізми Конструкції штовхачів
Рис.4.2 Рис.4.3
За характером замикання кінематичної пари кулачок – штовхач, кулачкові механізми діляться на:
1/ кулачкові механізми з силовим замиканням /пружиною/, /рис.4.4,а/;
2/ кулачкові механізми з геометричним замиканням /паз в кулачку/, /рис.4.4,б/.
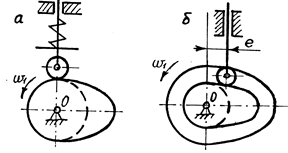 |
Замикання кулачкових механізмів
Рис.4.4
4.2. Закони руху веденої ланки. Фазові кути.
Рух ведучої і веденої ланки кулачкового механізму може бути заданий аналітично у вигляді рівнянь руху або графічно у вигляді діаграм переміщень, швидкостей чи прискорень. Характер цих рівнянь та діаграм може бути різним. Закон руху має задовольняти основні вимоги робочого процесу, зв’язаного з
рухом ланки механізму.
Розглянемо найбільш поширені в техніці закони /графіки/ руху веденої ланки кулачкового механізму. Розрізняють закони руху ведених ланок кулачкових механізмів трьох видів:
1/ з жорсткими ударами /рис.4.5,а/;
2/ з м’якими ударами /рис.4.5,б/;
3/ без ударів /рис.4.5,г/.
 |
Закони руху веденої ланки
Рис.4.5
При законі руху штовхача /рис.4.5,в/ діаграми швидкостей та прискорень не мають точок розриву, а тому рух відбувається без ударів.
Як видно із наведених діаграм, при проектуванні кулачкових механізмів з динамічної точки зору доцільно виходити з графіка прискорень.
Рух штовхача за цикл складається із наступних фаз /рис.4.6/:
1/ віддалення /піднімання / 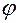 в штовхача від центра обертання кулачка на повну величину ходу, кулачок при цьому повертається на кут віддалення
в штовхача від центра обертання кулачка на повну величину ходу, кулачок при цьому повертається на кут віддалення 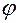 в;
в;
2/ штовхач залишається нерухомим у піднятому положенні – дальньому вистої 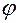 д, кулачок повертається на кут дальнього вистою
д, кулачок повертається на кут дальнього вистою 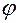 д;
д;
3/ наближення /опускання/ 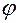 н штовхача на величину ходу, кулачок повертається на кут наближення
н штовхача на величину ходу, кулачок повертається на кут наближення 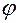 н;
н;
4/ штовхач залишається нерухомим у початковому положенні –
ближньому вистої 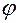 б, кулачок повертається на кут ближнього вистою
б, кулачок повертається на кут ближнього вистою 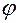 б.
б.
Кути 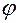 в,
в, 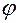 д,
д, 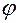 н,
н, 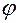 б повороту кулачка, в межах яких штовхач віддаляється, знаходиться у дальньому вистої, наближається і знаходиться у ближньому вистої, називається фазовими кутами.
б повороту кулачка, в межах яких штовхач віддаляється, знаходиться у дальньому вистої, наближається і знаходиться у ближньому вистої, називається фазовими кутами.
4.3. Кінематичний аналіз кулачкових механізмів.
При вивченні кулачкових механізмів може бути поставлено два завдання:
1/ аналіз /дослідження/ існуючих кулачкових механізмів;
2/ синтез /проектування/ нових кулачкових механізмів за заданими умовами.
Аналіз кулачкових механізмів полягає у визначенні закону руху штовхача за відомою кінематичною схемою механізму /тобто профіль кулачка заданий/, /рис.4.6,а/.
Кінематичне дослідження кулачкових механізмів можна виконати аналітичними і графічними методами. Найчастіше застосовують графічні методи: метод графіків /діаграм/ та метод планів.
 |
Кінематичний аналіз кулачкових механізмів методом діаграм
Рис.4.6
4.3.1. Аналіз методом діаграм.
Почнемо аналіз кулачкових механізмів з методу кінематичних діаграм.
Розмітимо переміщення з точки А штовхача умовної теоретичної схеми кулачкового механізму /рис.4.6,а/.
Розмітивши переміщення точки А штовхача, побудуємо графік її руху /переміщення/ /рис.4.6,б/.
Відкладемо на осі абсцис прямокутної системи координат у деякому масштабі 
 кути повороту кулачка, відповідно до розмітки його профілю; по осі ординат у масштабі
кути повороту кулачка, відповідно до розмітки його профілю; по осі ординат у масштабі  s відповідні переміщення точки А штовхача від його нижнього положення. Сполучивши плавною кривою кінці ординат, отримаємо діаграму переміщення штовхача залежно від кута повороту кулачка.
s відповідні переміщення точки А штовхача від його нижнього положення. Сполучивши плавною кривою кінці ординат, отримаємо діаграму переміщення штовхача залежно від кута повороту кулачка.
Затим, відомими методами графічного диференціювання можна побудувати діаграми аналогів швидкості та прискорення штовхача /рис. 4.5, в,г/.
Побудова діаграм виконується методами, аналогічно, викладеним при кінематичному дослідженні важільних механізмів методом діаграм.
Масштаби побудованих діаграм визначаються за формулами:
Масштаб кута повороту кулачка

 =
=
 ; /4.1/
; /4.1/
Масштаб переміщення
 S =
S = е,
е, 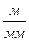 ; /4.2/
; /4.2/
масштаб аналогів швидкостей

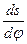 =
=  ,
, 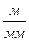 ; /4.3/
; /4.3/
масштаб аналогів прискорень

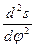 =
= 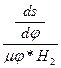 ,
, 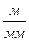 ; /4.4/
; /4.4/
масштаб швидкості
 v =
v = 
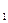 .
. 
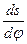 ,
, 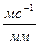 ; /4.5/
; /4.5/
масштаб прискорення

 =
=  *
*
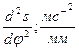 /4.6/
/4.6/
4.3.2. Аналіз методом планів.
Якщо потрібно більш точно визначити швидкість та прискорення штовхача в заданому положенні кулачкового механізму, то застосовують метод планів. Для цього будуємо замінюючий механізм, тобто кінематичну пару ІУ класу замінимо умовно кінематичними парами У класу. Кожному окремому положенню кулачкового механізму буде відповідати свій замінюючий механізм. Для його побудови необхідно визначити положення центра кривизни кулачка. В центрі кривизни кулачка /рис. 4.7, а/, та в центрі ролика ставляться кінематичні пари У класу і з’єднаються між собою, та центр обертання кулачка з’єднується з центром його кривизни. Отримаємо замінюючий механізм.
Затим будуємо план швидкостей в масштабі  v та прискорень в масштабі
v та прискорень в масштабі 
 для замінюючого механізму, як для звичайного кривошипно шатунного механізму /рис. 4.7, б, в/.
для замінюючого механізму, як для звичайного кривошипно шатунного механізму /рис. 4.7, б, в/.
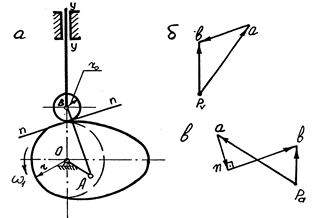 |
Кінематичний аналіз кулачкових механізмів методом планів
Рис. 8.7
4.4. Кінематичний синтез кулачкових механізмів з роликовим та тарілчастим штовхачами.
Кінематичний синтез кулачкових механізмів полягає в тому, щоб за необхідними умовами побудувати профіль кулачка. До числа необхідних умов входять наступні вихідні дані:
1/ хід штовхача;
2/ найменший /початковий/ радіус профілю кулачка;
3/ фазові кути;
4/ закон руху штовхача;
5/ закон руху кулачка.
На рис. 4.8. у певному масштабі побудовано діаграму переміщень штовхача (µs,µφ)
 |
Діаграма переміщень штовхача
Рис. 9.1
По осі абсцис відкладені фазові кути: кут віддалення φв  , кут дальнього вистою φд
, кут дальнього вистою φд  , кут наближення φ н
, кут наближення φ н  . По осі ординат – переміщення штовхача на кожному фазовому куті. Керуючись цією діаграмою, розмітимо хід штовхача. Для цього поділимо фазові кути φ в
. По осі ординат – переміщення штовхача на кожному фазовому куті. Керуючись цією діаграмою, розмітимо хід штовхача. Для цього поділимо фазові кути φ в  і φ н
і φ н  на декілька рівних частин, наприклад, на чотири. Позначимо точки 0, 1, 2, 3... 9. Проведемо із точок 1, 2, 3... вертикальні лінії до перетину із діаграмою переміщення штовхача. На перетині отримаємо точки 1’, 2`, 3` … Якщо кулачок повертається із положення 0 в положення 1, то штовхач віддалиться на величину 1-1`, при повороті кулачка в положення 2 штовхач віддалиться на величину 2-2` і т.д.
на декілька рівних частин, наприклад, на чотири. Позначимо точки 0, 1, 2, 3... 9. Проведемо із точок 1, 2, 3... вертикальні лінії до перетину із діаграмою переміщення штовхача. На перетині отримаємо точки 1’, 2`, 3` … Якщо кулачок повертається із положення 0 в положення 1, то штовхач віддалиться на величину 1-1`, при повороті кулачка в положення 2 штовхач віддалиться на величину 2-2` і т.д.
Розглянемо профілювання кулачкового механізму з роликовим штовхачем.
Побудову профілю кулачка будемо виконувати методом інверсії, або методом оберненого руху. Кулачковому механізму надано кутову швидкість -  ωk , тоді кулачок зупиниться, а штовхач почне обертатися навколо кулачка в напрямі, протилежному обертанню кулачка, з кутовою швидкістю ωk
ωk , тоді кулачок зупиниться, а штовхач почне обертатися навколо кулачка в напрямі, протилежному обертанню кулачка, з кутовою швидкістю ωk 
Вибираємо точку 0 – положення центра обертання кулачка. Із центра 0 найменшим /початковим/ радіусом профілю кулачка r0 в масштабі описуємо основне /початкове/ коло /рис. 4.9, а/.
Профілювання кулачка
 |
Рис. 4.9
Нехай штовхач обертається навколо основного кола профілю кулачка так, що точка А0 штовхача переміщується відносно основного кола у відповідності з діаграмою руху штовхача /рис. 4.8/. Точка А0 опише необхідний теоретичний профіль кулачка. Для практичного знаходження профілю кулачка поступаємо так. Відкладемо, починаючи від точки А0 в напрямі, зворотному обертанню кулачка, фазові кути φв  , φд
, φд  , φн
, φн  . Радіальними лініями поділимо кути φв
. Радіальними лініями поділимо кути φв  і φн
і φн на стільки рівних частин, на скільки вони поділені на діаграмі руху штовхача /рис. 9.1/, наприклад, на чотири. Отримаємо на основному колі точки 1,2,3... 9.
на стільки рівних частин, на скільки вони поділені на діаграмі руху штовхача /рис. 9.1/, наприклад, на чотири. Отримаємо на основному колі точки 1,2,3... 9.
На променях 01, 02, 03... відкладемо від початкового кола, переміщення штовхача 1-1`, 2-2`, 3-3` … взяті із діаграми руху /рис. 4.8/. З’єднаємо плавною кривою отримані, на відповідних променях, точки 1`, 2`, 3`… отримаємо частину профіля кулачка на кутах φв  і φн.
і φн. 

 Профілі кулачка, що відповідають фазам дальнього вистою φд і ближнього вистою φб будуть обмежені дугами кіл, які описано із центра 0 радіусами 0-4 і ОА0.
Профілі кулачка, що відповідають фазам дальнього вистою φд і ближнього вистою φб будуть обмежені дугами кіл, які описано із центра 0 радіусами 0-4 і ОА0.
Таким чином, отримаємо повний теоретичний профіль кулачка. Якщо цей профіль обертати з кутовою швидкістю ω1, то можна стверджувати, що точка штовхача А0 здійснюватиме завданий закон руху, відповідно діаграмі /рис. 4.8/.
Якщо штовхач закінчується роликом, то будуємо еквідистантний центровому /теоретичному / профілю, практичний /конструктивний/профіль кулачка.
Радіус rp ролика визначаємо
rp = /0,3…0,4/ r0 /4.7/
Тепер штовхач разом з роликом обкатуємо по теоретичному профілю кулачка, так щоб центр ролика знаходився на теоретичному профілі. Для цього ніжку циркуля ставимо на теоретичний профіль і радіусом ролика rp робимо кола /засічки/ до їх взаємного перетину.
Вписавши плавну криву на відстані радіуса ролика rp від теоретичного профілю, отримаємо практичний, або конструктивний профіль кулачка.
Розглянемо профілювання кулачкового механізму з тарілчастим штовхачем, коли вісь штовхача зміщена відносно осі обертання кулачка /кулачковий механізм з ексцентриситетом/.
Побудову будемо виконувати методом інверсії, тобто аналогічно побудові кулачкового механізму з роликовим штовхачем.
В точках 1', 2', 3'... проведемо прямі, перпендикулярні до відповідних дотичних, до взаємного перетину. Впишемо плавну криву в побудований багатокутник. Це і буде теоретичний і одночасно, для кулачкового механізму з тарілчастим штовхачем, конструктивний профіль кулачка.
4.5. Кут тиску та кут передачі руху.
Одним з найважливіших розрахункових параметрів кулачкового механізму є кут передачі руху γ або кут тиску α.
Нехай F сила, з якою кулачок 1 діє на штовхач 2 /рис. 4.10/.
Якщо не враховувати тертя, то сила F направлена по загальній нормалі n-n в точці дотику кулачка і штовхача.
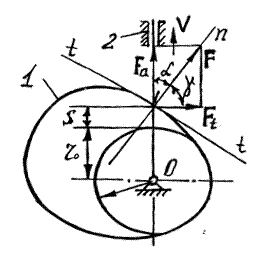 |
Кут тиску та передачі руху.
Рис.4.10
Розкладемо силу F на дві складові: Fa – направлена паралельно руху штовхача і Ft – перпендикулярно руху штовхача. Сила Fa буде рушійною силою, яка рухає штовхач; сила Ft буде згинати штовхач і викликати тертя в напрямних. Очевидно, що механізм буде працювати тим краще, чим більша сила Fa і менша сила Ft.Кут, утворений силою F з напрямом швидкості V, називається кутом тиску α. Із рис. 4.10 маємо:
Ft = F sin α,
Fa = F cos α. /4.8/
Із відношення /9.2/ видно, що кулачковий механізм буде працювати тим краще, чим менший кут тиску.
В різних положеннях механізму кут тиску не однаковий. Зменшення кута тиску приводить до збільшення габаритів кулачка. Раціональне його значення вибирається виходячи із досвіду експлуатації механізмів.
Для кулачкових механізмів: з штовхачем, що рухається поступально
α 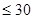 : з коромисловим штовхачем α
: з коромисловим штовхачем α  : з тарілчастим штовхачем α
: з тарілчастим штовхачем α 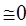 .
.
Додатковий кут до 90, тобто кут між силою F і силою Ft, називається кутом передачі руху γ
γ = 90 – α. /4.9/
4.6. Динамічний синтез кулачкових механізмів.
Існує безліч кулачкових механізмів, які задовольняють заданим законам руху штовхача. Раціональним вирішенням задачі слід вважати ту, при якій механізм має найменші розміри і являється придатним як з конструктивної точки зору, так і у відношенні міцності. При кінематичному синтезі задаються наперед значенням початкового /найменшого/ радіуса r0 профілю кулачка. При динамічному синтезі слід попередньо користуватися вихідними даними задачі, наприклад, заданим найбільшим значення кута тиску α max /або найменшим значенням кута передачі руху γ min /, знайти значення найменшого /початкового/ радіуса профілю кулачка r0. Цим самим зводимо розв’язування задачі динамічного синтезу кулачкових механізмів до уже відомої нам задачі кінематичного синтезу.
Визначення початкового радіуса профілю кулачка для кулачкових механізмів з роликовим та тарілчастим штовхачами викладено в [3, 4].
Тема 5. Зубчасті механізми
5.1. Типи зубчастих механізмів. Передаточні відношення простих зубчастих передач. Основна теорема зачеплення.
Механізм, призначений для передавання обертового руху від одного вала до іншого за допомогою зубчастих коліс, що перебувають у зачепленні з заданим відношенням кутових швидкостей, називають зубчастою передачею.
Зубчасті передачі діляться на плоскі і просторові. До плоских відносяться передачі з циліндричними зубчастими колесами. У таких передачах осі валів паралельні. До просторових відносяться передачі: конічні, гвинтові і черв’ячні. У них осі валів перетинаються, або схрещуються. Циліндричні зубчасті передачі бувають зовнішнього, внутрішнього або рейкового зачеплення. В залежності від форми зубів коліс передачі можуть бути прямозубими або косозубими.
В сучасній техніці зубчасті механізми мають широке застосування /автомобілі, трактори, екскаватори, верстати і ін./.
Обертання зубчастих коліс проходить в загальному випадку з різними кутовими швидкостями ω1 і ω2. Відношення цих кутових швидкостей називається передаточним відношенням і позначається буквою U.
 Будемо називати передаточним відношенням U12 від колеса 1 і до колеса 2 величину /5.1/
Будемо називати передаточним відношенням U12 від колеса 1 і до колеса 2 величину /5.1/
Менше /вхідне/ зубчасте колесо в зубчастій передачі називають шестернею. Передаточне відношення слід вважати від’ємним, якщо колеса обертаються в різні сторони. Такі колеса утворюють зубчасту передачу зовнішнього зачеплення /рис. 5.1, а/
 Зубчасті передачі
Зубчасті передачі
а – зовнішнє зачеплення; б – внутрішнє зачеплення; в – рейкове зачеплення
Рис. 5.1
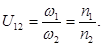 У випадку внутрішнього зачеплення /рис. 5.1, б/ обидва колеса обертаються в одну сторону і передаточне відношення буде додатнім якщо одне із коліс виготовлене у вигляді зубчастої рейки /рис.5.1, в/, то U=0, або U=∞. У більшості випадків U12=const, тоді підвищення кутових швидкостей можна замінити відношенням чисел обертів
У випадку внутрішнього зачеплення /рис. 5.1, б/ обидва колеса обертаються в одну сторону і передаточне відношення буде додатнім якщо одне із коліс виготовлене у вигляді зубчастої рейки /рис.5.1, в/, то U=0, або U=∞. У більшості випадків U12=const, тоді підвищення кутових швидкостей можна замінити відношенням чисел обертів
/5.2/
Лінія перетину однієї із бокових поверхонь зуба площиною, перпендику-лярною до осі колеса, називається терцевим профілем зуба. Очевидно, що профілі зубів двох коліс, які передають обертальний рух з заданим відношенням кутових швидкостей, не можуть бути довільними. Основна теорема зачеплення і встановлює умову, якій повинні задовольняти профілі зубів, щоб передача працювала (U = coпst). Нехай зуби коліс 1 і 2 /рис. 5.2/ обертаються з кутовими швидкостями ω1 і ω2 і дотикаються один до одного в т. К. Точка К належить одночасно зубу колеса 1 і зубу колеса 2. Швидкість т. К, що належить колесу 1 направлена перпендикулярно до радіуса 01К в сторону ω1 і за величиною рівна
 /5.3/
/5.3/
 Зубчасте зачеплення
Зубчасте зачеплення
Рис.5.2
Швидкість т. К, що належить колесу 2 перпендикулярна радіусу 02К рівна
 /5.4/
/5.4/
Проведемо через т.К загальну дотичну Т-Т і загальну нормаль N-N. Відмітимо т. Р перетину цієї нормалі з лінією центрів 0102. Із центрів 01і 02 опустимо перпендикуляри на нормаль N-N, отримаємо точки L1 та L2.
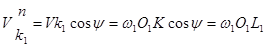 Швидкість Vk1 розкладемо на два напрямки: по N-N і по Т-Т. Нормальна складова швидкості /5.5/
Швидкість Vk1 розкладемо на два напрямки: по N-N і по Т-Т. Нормальна складова швидкості /5.5/
 Аналогічно отримаємо:
Аналогічно отримаємо:
/5.6/
 Для того, щоб зуби коліс не відходили один від одного і не врізались один в другий потрібно, щоб нормальні складові швидкостей
Для того, щоб зуби коліс не відходили один від одного і не врізались один в другий потрібно, щоб нормальні складові швидкостей 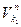 і
і  були рівні між собою за величиною і мали однаковий напрям
були рівні між собою за величиною і мали однаковий напрям
/5.7/
Підставимо в /5.7/ значення із /5.5/ і /5.6/, отримаємо:
ω1O1L1=ω2O2L2. / 5.8 /
 Звідси маємо:
Звідси маємо:
/5.9/
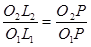 Якщо трикутники О1 і L1P і O2 L2P подібні, то можна записати:
Якщо трикутники О1 і L1P і O2 L2P подібні, то можна записати:
. /5.10/
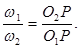 Замінивши відношення
Замінивши відношення 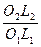 в /5.9/ із /5.10/ отримаємо:
в /5.9/ із /5.10/ отримаємо:
/5.11/
З рівняння /5.11/ випливає формулювання основної теореми зачеплення – теорема Вілліса.
Загальна нормаль до профілів зубів в точці їх дотику ділить віддаль між центрами обертання зубчастих коліс на частини, обернено пропорційні їх кутовим швидкостям.
Точка Р називається полюсом зачеплення. При ω1/ω2=coпst, на основі /5.11/ знаходимо, що 02Р/01Р = coпst, тобто полюс зачеплення т.Р на лінії центрів займає стале положення. У випадку передачі обертального руху з сталим відношенням кутових швидкостей, профілі зубів повинні бути підібрані так, щоб загальна нормаль до них в будь – якій точці дотику К завжди проходила через одну і ту ж точку на лінії центрів.
5.2 Евольвента кола та її властивості.
Евольвентою кола – називається крива, яку описує будь – яка точка прямої лінії, що котиться по колу без ковзання. Це коло називається основним, а пряма, що перекочується по колу твірною, або виробляючою прямою /рис. 5.3/.
 Нехай пряма N-N котиться по основному колу радіуса rь без ковзання. Точка К описує евольвенту. Біжучий радіус – вектор точки Кх евольвенти позначимо rx. Початковий радіус – вектор евольвенти Oko=rb. Гострий кут між дотичною до евольвенти в точці Кх і її радіусом – вектором Окх позначимо αx. Кут Ох між початковим радіусом – вектором евольвенти Око і її біжучим радіусом Окх, називається евольвент ним кутом або інволютою кута αx, тобто /5.12/
Нехай пряма N-N котиться по основному колу радіуса rь без ковзання. Точка К описує евольвенту. Біжучий радіус – вектор точки Кх евольвенти позначимо rx. Початковий радіус – вектор евольвенти Oko=rb. Гострий кут між дотичною до евольвенти в точці Кх і її радіусом – вектором Окх позначимо αx. Кут Ох між початковим радіусом – вектором евольвенти Око і її біжучим радіусом Окх, називається евольвент ним кутом або інволютою кута αx, тобто /5.12/
 Евольвента кола
Евольвента кола
Рис.5.3
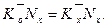 Будь – яка точка евольвенти визначається радіусом-вектора rx і евольвент ним кутом θх. Оскільки пряма N-N котиться по основному колу без ковзання, то можна скласти рівність /5.13/
Будь – яка точка евольвенти визначається радіусом-вектора rx і евольвент ним кутом θх. Оскільки пряма N-N котиться по основному колу без ковзання, то можна скласти рівність /5.13/
Із прямокутного трикутника OkxNx маємо:

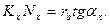 /5.14/
/5.14/
Знайдемо дуги знайдемо:
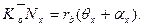 /5.15/ Підставимо значення із /5.14/ і /5.15/ в /5.13/, отримаємо:
/5.15/ Підставимо значення із /5.14/ і /5.15/ в /5.13/, отримаємо:
rb tgαx=rb(θx+αx). /5.16/ Розділимо обидві частини рівняння /5.16/ на r b, отримаємо:
θx+αx=tgαx, або
θx=tgαx-αx. /5.17/
Використавши позначення в рівнянні /5.12/, отримаємо
inVαx=tgαx-αx, або
Ox=tgαx-αx=inVαx. /5.18/
Зв’язок між rx і αx запишемо із трикутника KxONx
rx=  . /5.19/
. /5.19/
Рівняння /5.18/ і /5.19/ називаються параметричними рівняннями евольвенти.
Властивості евольвенти:
1/ евольвента – симетрична крива, яка має дві вітки, що збігаються у початковій точці Ко;
2/ будь – які дотичні NN до основного кола є нормалями до евольвенти у відповідних точках Кх;
3/ основне коло є геометричним місцем центрів кривизна евольвент описаних прямою NN, тобто їх еволютою, а значить вектор KxNx є радіусом кривизна евольвенти у точці Кх.
5. 3. Основні розміри циліндричних зубчастих коліс.
На розміри окремих елементів зубчастого колеса встановлені певні норми і стандарти. Зубчасті колеса, виготовлені за цими нормами, називають нормальними зубчастими колесами. Розглянемо переріз нормального зубчастого колеса площиною, перпендикулярною осі обертання.
Відстань між однойменними профілями сусідніх зубів, виміряна по дузі кола з центром на осі обертання коліс, називається коловим кроком зубів колеса /Р/. Цю саму відстань, виміряну по дузі основного кола, називають основним коловим кроком / Pb /, а відповідну дугу, виміряну по початковому колу, називають початковим коловим кроком / Pw / /рис.5.4/.
Такі два кола, що дотикаються і при обертанні зубчастих коліс котяться одне по другому без ковзання, називаються початковими колами.
Число зубів колеса позначимо Z, радіус початкового кола r w.
Для кожного колеса можна записати
2π rw1=PwZ1, /5.20/
2π rw2 = PwZ2. /5.21/
 Розділимо /5.21/ на /5.20/
Розділимо /5.21/ на /5.20/
. /5.22/
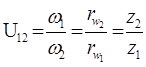 Співставляючи /5.21/ і /5.22/ із /5.11/, і прийнявши до уваги, що 01Р =rw1 і О2Р = rw2, отримаємо:
Співставляючи /5.21/ і /5.22/ із /5.11/, і прийнявши до уваги, що 01Р =rw1 і О2Р = rw2, отримаємо:
. /5.23/
 При проектуванні зубчастих коліс виходять не з кроку Pw, а з величини
При проектуванні зубчастих коліс виходять не з кроку Pw, а з величини
. /5.24/
яка називається торцевим модулем зубів.
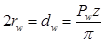 Із формули /5.20/ для будь – якого зубчастого колеса маємо:
Із формули /5.20/ для будь – якого зубчастого колеса маємо:
. /5.25/
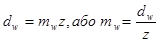 Враховуючи /5.24/, отримаємо:
Враховуючи /5.24/, отримаємо:
. /5.26/
Модуль показує число мм діаметра ділильного /початкового/ кола, що припадає на один зуб. Модуль величина стандартна.
Величина, обертання модулю, називається пітчем /США, Англія/ / pitch – крок Pd/, Pd = z/d, де d - діаметр ділильного кола в дюймах. Зв’язок модуля з пітчем 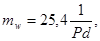 мм.
мм.
Ділильне /початкове/ коло ділить переріз зуба по висоті на дві частини: ніжку і головку. Радіальна відстань h між колом вершини і колом западини вимірює висоту зуба.
Коло, що обмежує зуби зовні, називається колом вершини зубів, а коло, що обмежує западини – колом западин.
Висота зуба h складається із висоти головки ha і висоти ножки hf
h=ha+hf /5.27/
Згідно стандарту розміри зубів нормальної висоти такі:
ha=m; hf=1,25m; h=2,25m /5.28/
 |
Циліндричні зубчасті колеса
Рис.5.4.
 Товщина зуба Sw по початковому колу і ширини западини ew дорівнюють половині кроку Pw /5.29/
Товщина зуба Sw по початковому колу і ширини западини ew дорівнюють половині кроку Pw /5.29/
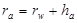 Радіус ra кола вершин /5.30/
Радіус ra кола вершин /5.30/
Радіус кола западин Zf = Zw - hf /5.31/
Для нормальних зубчастих коліс ділильне коло співпадає з початковим.
Коло, по якому необхідно котити без ковзання дотичну пряму, щоб отримати евольвенту /профіль зуба/, називається основним колом.
 Із трикутника 0І N1P маємо / 01N1=rb /
Із трикутника 0І N1P маємо / 01N1=rb /
/5.32/
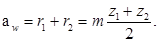 Визначимо відстань між центрами коліс ОIО2
Визначимо відстань між центрами коліс ОIО2
/5.33/
5.4 Геометрія евольвентного зачеплення.
Через точку Р – полюс зачеплення проведемо загальну дотичну Т-Т до початкових кіл і загальну нормаль N-N до профілів зубів, що дотикаються в цій точці /рис. 5.4/. Кут, утворений прямими ТТ і NN, називається кутом зачеплення αw. Геометричне місце точок дотику профілів зубів двох спряжених коліс, називається активною лінією зачеплення, ab.
Зачеплення розпочинається в точці a, в якій коло вершин зубів веденого колеса перетинає лінію зачеплення і закінчується в точці в, в якій лінію зачеплення перетинає коло вершин зубів ведучого колеса.
Геометрія евольвентного зачеплення викладена в [1,2,3,4].
5. 5. Косозубі циліндричні колеса. Основні параметри.
У прямозубих колесах зубці стикаються одночасно по всій довжині зубця, а тому перехід зачеплення з зубця на зубець супроводжується ударом і шумом. Несталість кроку, неточність профілю та інші похибки, які були допущені при виготовленні коліс та при монтажі їх, можуть значно погіршити умови роботи прямозубої передачі. Крім цього, прямозубі колеса мають порівняно невеликий коефіцієнт перекриття. Щоб збільшити коефіцієнт перекриття і зменшити чутливість зубців до похибок виготовлення і монтажу, прямозубі колеса замінюють колесами з косими або шевронними зубцями. У косозубих коліс зубці розміщенні під деяким кутом β до твірної циліндра колеса /рис. 5.5/, /осі обертання/.
В торцевому перерізі профіль зуба евольвент ний. Позначимо в цьому перерізі крок Ps, модуль ms, а в перерізі по нормалі N-N – крок P n, модуль mn. Кут зачеплення αw, ширина колеса – b.
Зв’язок кроку і модуля аналогічний як і для прямозубого колеса
 Pn=πmn, Ps=πms. /5.34/
Pn=πmn, Ps=πms. /5.34/
Із трикутника АВС /рис.5.5/ маємо: /5.35/
 Торцевий модуль зв’язаний з нормальним відповідно
Торцевий модуль зв’язаний з нормальним відповідно
/5.36/
Кут нахилу зубців приймають β = 8...30º.
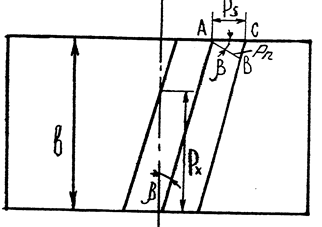 Косозубе колесо
Косозубе колесо
Рис.11.5
Стандартним приймається нормальний модуль. Геометричні параметри косозубого колеса, в нормальному перерізі, визначають за тими же формулами, що і для прямозубого колеса.
5.6. Конічні зубчасті передачі. Основні параметри.
Конічні зубчасті передачі застосовуються для передавання рухів між валами, що перетинаються /часто під кутом 90/. Аксоїдами у відносному русі конічних зубчастих коліс /рис. 5.6/ є два конуси А і В. Ці конуси за аналогією з центроїдами /початковими колами циліндричних коліс/ називаються початковими конусами.
 Конічна зубчаста передача
Конічна зубчаста передача
Рис.5.6
Спільна вершина цих конусів знаходиться в т. О, на перетині їх осей.
Передаточне відношення U12 зберігатиметься сталим у тому разі коли початкові конуси котитимуться один по одному без ковзання. Для цього досить, щоб швидкості точки стикання К, яка належить обом конусам, були рівні, тобто V1=V2. Оскільки V1=ω1r1, a V2=w2r2, то
ω1r1=ω2 r 2. / 5.37 /
Із прямокутного трикутника /рис. 5.6/
r1=KO sin δ1; r2=KO sin δ2. /5.38/
Якщо кути при вершинах початкових конусів δ1+ δ2 = 90º, то загальний вираз
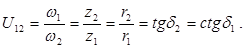 передаточного відношення можна записати:
передаточного відношення можна записати:
/5.39/
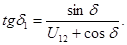 Кут δ1 при вершині конуса можна знайти аналогічно як для фрикційної конічної передачі
Кут δ1 при вершині конуса можна знайти аналогічно як для фрикційної конічної передачі
/5.40/
Подамо формули для визначення числа зубців еквівалентних циліндрич-них коліс.
Для конічного зачеплення, при δ = 90º, остаточно маємо:
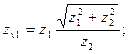 | 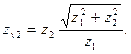 |
/5.41/
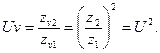 З рівняння /5.41/ випливає: /5.42/
З рівняння /5.41/ випливає: /5.42/
Таким чином, зачеплення конічних коліс з числами зубів z1 i z2 еквівалентно зачепленню циліндричних коліс з еквівалентними числами зубів zv1 і zv2.
Конічні колеса бувають прямозубі, косозубі і гіпоїдні. Модуль і крок в них змінюється по довжині зуба. За стандартну величину береться модуль в зовнішньому найбільшому торцевому перерізі.
5 .7. Черв’ячна передача.
Для передачі руху між валами, які не паралельні і не перетинаються, а схрещуються, найбільш широко застосовуються черв’ячні передачі. Один з елементів передачі, має форму одновиткового або багатовиткового гвинта, називається безкінечним гвинтом, або черв’яком. Черв’ячне колесо, яке з ним зачіплюється, має зубці, що являють собою виступи гвинтової різьби гайки, яка відповідає гвинту /рис.5.7/. Кут схрещування в більшості випадків дорівнює 90º.
В залежності від способу утворення поверхні черв’яка розрізняють два основні типи черв’ячної передачі:
а/ з архімедовим черв’яком, що має прямобічний профіль в осьовому перерізі;
б/ з евольвентним черв’яком, що має прямобічний профіль на деякій віддалі від осі і криволінійний випуклий профіль в осьовому перерізі.
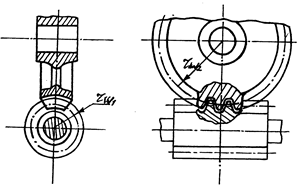 Черв’ячна передача
Черв’ячна передача
Рис.5.7
Користуючись кінематичною аналогією між черв’ячною і рейковою передачами, можна легко встановити зв'язок між основними параметрами черв’ячної передачі.
 В разі зачеплення черв’яка з рейкою її зубці при обертанні черв’яка навколо осі переміщаються вздовж неї, причому при одному оберті черв’яка рейка переміщається на крок Р зачеплення, помножений на число ниток Z черв’яка, тобто на висоту підйому h нитки черв’яка. Таким чином, при числі обертів на хвилину n1, швидкість V1 переміщення рейки дорівнюватиме:
В разі зачеплення черв’яка з рейкою її зубці при обертанні черв’яка навколо осі переміщаються вздовж неї, причому при одному оберті черв’яка рейка переміщається на крок Р зачеплення, помножений на число ниток Z черв’яка, тобто на висоту підйому h нитки черв’яка. Таким чином, при числі обертів на хвилину n1, швидкість V1 переміщення рейки дорівнюватиме:
/5.43/

 При зачепленні черв’яка з черв’ячним колесом колова швидкість V2 профілю зубця на колесі /5.44/
При зачепленні черв’яка з черв’ячним колесом колова швидкість V2 профілю зубця на колесі /5.44/
В спільній точці дотику V1 = V2, або. /5.45/
Для гвинтової лінії черв’яка залежність між висотою підйому h і кутом λ підйому гвинтової лінії можна встановити із прямокутного трикутника
h=2πrw1tg λ. /5.46/
Підставимо значення h із /5.46/ в формулу /5.45/ і після нескладних перетворень отримуємо: 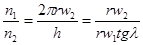 , /5.47/
, /5.47/
оскільки 2πr w2= Z2P а h= Z1P, то рівняння /5.47/ можна записати у вигляді
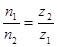 /5.48/
/5.48/
Передаточне відношення  /5.49/
/5.49/
Для черв’ячних передач передаточне відношення U =10…80. профілі зубців колеса та їх розміри в головному перерізі роблять такими самими, як і для циліндричних коліс. Висоту зубців беруть стандартну h=2,25m Кут зачеплення α = 200, або 150. Кут підйому гвинтової лінії l= 5... 200. Число заходів черв’ячка Z1 = 1...6. При α =150, Z2 ≥ 24, при α = 200, Z2 ≥36. Коефіцієнт корисної дії = 0,7... 0,9. Число модулів в початковому діаметрі черв’яка називається коефіцієнтом відносного діаметра черв’яка
q= 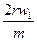 /5.50/
/5.50/
В більшості випадків q = 8...16.
В черв’ячних передачах стандартним є осьовий модуль черв’яка, який дорівнює торцевому модулю колеса. Черв’ячна передача є самогальмівною. Вхідною ланкою передачі завжди являється черв’як.
Якщо частину дуги початкового кола колеса прийнята за початкову лінію черв’яка, то отримаємо глобоїдну передачу. В цій передачі глобоїдну /вогнуту/ форму мають як зубці колеса, так і витки черв’яка. Гвинтові поверхні глобоїдного черв’яка мають різний крок, який зменшується від середини частини її кінців. Черв’ячна передача з глобоїдним черв’яком дозволяє при однакових габаритах передавати значно більшу потужність порівняно з передачею з циліндричним черв’яком і має високий коефіцієнт корисної дії.
5.8 Передаточні відношення складних зубчастих передач з нерухомими осями.
Зубчасті механізми, в яких відбувається зменшення кутових швидкостей при передачі від ведучої ланки, називаються редукторами, а зубчасті механізми, які збільшують кутову швидкість, називаються мультиплікаторами.
Зубчаста передача у вигляді пари коліс, що зчіплюються /одноступінчаста передача/ може відтворити лише невеликі значення передаточних відношень.
Передаточне відношення U12 пари зубчастих коліс, як відомо, виражається формулою:  /5.51/
/5.51/
Отже, з конструктивного боку U12 залежить від числа зубів Z2 і Z1, а значить обмежене деякою величиною. На практиці для пари зубчастих коліс U12 = 1...10.
Якщо за умовами роботи треба відтворювати велике передаточне відношення, то передача руху від ведучого вала до веденого здійснюється за допомогою кількох проміжних валів, на яких закріплюють зубчасті колеса.
Багатоступінчасті зубчасті передачі відносяться до складних зубчастих механізмів. Складні зубчасті механізми бувають з нерухомими і рухомими осями.
Розглянемо складні зубчасті механізми з нерухомими осями /рис. 5.8/
Такі механізми діляться на: ступінчасті /паралельна серія//рис. 5.8/, та рядові /послідовна серія зубчастих коліс/ /рис. 5.8, б/.
Передаточне відношення зубчастого механізму з паралельною серією зубчастих коліс /рис. 5.8, а/

 /5.52/
/5.52/
Враховуючи /5.51/ вираз /5.52/ прийме вигляд:
 . /5.53/
. /5.53/
Передаточне відношення рядової серії
 /5.54/
/5.54/ 
Передаточне число для такого механізму дорівнює відношенню числа зубів останнього колеса до числа зубів першого колеса.
 |
Складні зубчасті механізми
Рис.5.8
5. 9. Зубчасті механізми з рухомими осями. Планетарні та диференціальні механізми.
Зубчасті механізми, у яких геометричні осі одного чи декількох коліс переміщуються у просторі називаються планетарними. Планетарні механізми з однією ступінню вільності називаються звичайними планетарними механізмами /рис. 5.9, а/.
Планетарні механізми з ступінню вільності два і більше, називається диференціальними /рис. 5.9, б/.
Зубчасті колеса 1і 3 називаються центральними або сонячними. Зубчасте колесо 2, вісь обертання якого обертається навколо другої осі називається сателітом. Ланка Н називається водилом. Центральне закріплене колесо 3 називається опорним.
Ступінь вільності таких механізмів визначається за формулою П.Л.Чебишева: W=3 n -2R5- R4
| n | P5 | P4 | |
| 0-1 | 1-2 | ||
| 2-H | 2-3 | ||
| H | H-0 | - | |
| Σ |
| n | P5 | P4 | ||
| 0-1 | 1-2 | |||
| 2- Н | 2-3 | |||
| 3-О | - | |||
| Н | Н-О | - | ||
| Σ | ||||
Планетарний механізм Диференціальний механізм
W=3*3-2*3-2=1 W=3*4-2*4-2=2
Будь яку диференціальну передачу можна перетворити в планетарну шляхом закріплення одного із коліс.
Зубчасте колесо 1 обертається навколо осі і знаходиться в зачепленні
разом з колесом 2. Колесо 2 знаходиться одночасно в двох рухах:в обертанні
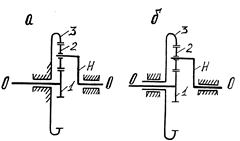 |
Зубчасті механізми з рухомими осями
а – планетарний механізм Джемса; б – диференціальний механізм
Рис. 5.9
разом з водилом Н і з кутовою швидкістю ωH навколо нерухомої спільної осі 0-0 механізму, залишаючись у той самий час у постійному зачепленні з колесами 1 та 3 і в обертанні з кутовою швидкістю ω2H навколо своєї власної осі. Зубчасте колесо 3 обертається в диференціальному механізмі і воно нерухоме /опорне/ в планетарному механізмі.
На рис 5.10 показано складний зубчастий механізм з рухомими осями з
зовнішнім зачепленням /рис. 5.10, а/ і внутрішнім зачепленням /5.10, б/. Якщо всі колеса механізму обертаються, то ступінь вільності – два і це буде диф
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 2155; Нарушение авторских прав?; Мы поможем в написании вашей работы!