Хвильова передача

Рис. 5.11

Під час обертання генератор 1 своїми роликами обкочує пружно деформований зубчастий вінець 3 по нерухомому центральному колесі 2 переміщуючи у коловому напрямі у бік власного обертання осей зачеплення, або хвилі деформації. При різних числах зубців 2 та гнучкого вінця 3 це приводить до обертання вінця, а отже і з'єднаного з ним веденого вала у напрямі, протилежному напряму обертання генератора 1.

Визначимо передаточне відношення хвильової передачі в планетарному одноступінчатому виконанні /рис. 5.11/.

	ω 1	ω 1- ω 1=0
	ω 2=0	ω 2- ω 1=- ω 1
	ω 3	ω 3- ω 1

Залежність між кутовими швидкостями ω₁ генератора I і /ведучої ланки/ та ω ₃ пружного вінця /веденої ланки / можна дістати, користуючись методом обертання руху. Для цього всьому механізму надамо кутову швидкість – ω ₁: при цьому в оберненій передачі генератор буде немов би зупинений, а гнучкий вінець і жорстке колесо обертатимуться в одному напрямі відповідно з кутовими швидкостями:

Передаточне відношення від колеса 2 до гнучкої ланки 3 в оберненому русі визначиться відношенням

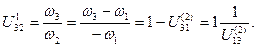/5.62/

З відношенням /5.62/ маємо:

_. /5.63/

Враховуючи, що передаточне відношення U ⁽¹⁾₃₂ в зображеній передачі визначається як і звичайної передачі відношенням чисел зубів, тобто 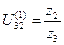і z₂>z₃, то рівняння /5.63/ остаточно прийме вид

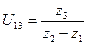_. /5.64/

5. 12 Проектування планетарних механізмів.

Планетарні механізми виконують звичайно з декількома сателітами, розміщеними на рівних відстанях один від одного. При числі сателітів, рівному k, вони повинні бути встановлені один відносно одного під кутами 2 p/ k.

При збільшенні числа сателітів навантаження на кожну пару зубів зменшується; це дозволяє застосовувати колеса менших розмірів, а тому і загальні габарити механізму зменшуються. Однак існує межа числа сателітів. Максимальне число сателітів може бути таким, щоб вершинами своїх зубів сателіти не торкалися один одного. Для того, щоб планетарний механізм можна було скласти, необхідно щоб зуби сателітів могли одночасно ввійти в зачеплення з зубами обох центральних коліс. Виконання цих і інших умов повинно бути враховано при проектуванні планетарних механізмів, яке зводиться до визначення числа зубів коліс, при заданому передаточному відношенні і підбору числа сателітів.

При проектуванні планетарного механізму необхідно виконати наступні умови: забезпечення заданого передаточного відношення, умову співвісності, умову складання, умову сусідства.

Розглянемо всі ці умови на прикладі редуктора Джемса /рис. 5.12/.

Забезпечення заданого передаточного відношення

Визначимо необхідне співвідношення між числом зубів коліс редуктора Джемса для забезпечення заданого передаточного відношення, використавши формулу передаточного відношення планетарної передачі /5.60/, отримаємо:

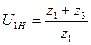. /5.65/

Умова співвісності.

Для виконання умови співвістиності необхідно щоб осі центральних

/сонячних/ коліс 1 і 3 і водила Н лежали на одній прямій /осі/ 00.

Із рис. 5.12 видно, що для виконання цієї умови необхідно забезпечити наступне співвідношення між радіусами коліс:

r₃=r₁+2r_2. /5.66/

Виразимо радіуси через модуль і числа зубів

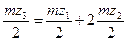_. /5.67/

Скоротивши це рівняння на m/2, отримаємо:

z₃ = z₁ + 2 z_{2 .} /5.68/

Звідки

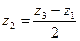. /5.69/

Редуктор Джемса

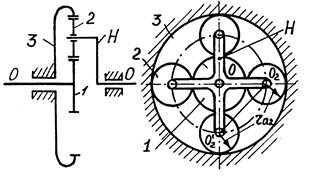_Рис.5.12

Таким чином число зубів сателітів залежить від числа зубів центральних коліс. Із рівняння /5.69/ випливає, що оскількі Z2повинно бути числом цілим, то числа зубів Z1 I Z3 повинні бути або обидва парними, або обидва непарними.

Умова складання.

При числі сателітів рівним одиниці, передача завжди може бути складена, якщо виконується умова співвісності. В загальному випадку при числі сателітів К>1 цієї умови уже недостатньо.

Для того щоб механізм, який включає К сателітів, міг бути складений,

тобто зуби сателітів одночасно могли ввійти в зачеплення з зубами обох центральних коліс, необхідно, щоб відношення суми чисел зубів центральних коліс до числа сателітів було цілим числом, тобто:

,

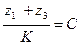де С – ціле число.

Умова сусідства.

Для забезпечення умови сусідства необхідно, щоб сусідні сателіти не черкалися головками зубців, тобто щоб відстань між центрами обертання сателітів була більшою двох радіусів кіл вершин, тобто

O₂O₂^`>2r_a2. /5.70/

Визначивши із рис.5.12 відстань O₂O₂^` і виразивши r_a2 через модуль і число зубів, знайдемо:

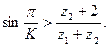/5.71/

Нерівність /5.71/ забезпечує умову сусідства, тобто умову не черкання сусідніми сателітами один одного.

5. 13 Методи нарізання зубів зубчастих коліс

Зубчасті колеса виготовляються багатьма способами. Всі ці способи можна віднести до двох методів виготовлення: метод копіювання, та метод обкатування.

Методи нарізання зубів зубчастих коліс викладені в [1,2,3,4].

5.14. Підрізування зубів. Найменше число зубів на колесі.

Розглянемо можливий випадок, коли вершина зуба колеса вкорінюється в тіло шестерні. При цьому зуби колеса защемлятимуться в западинах шестерні що викличе посилений знос зубів або їхню поломку. Щоб запобігти заклинанню зубів, ніжку зуба шестерні треба підрізати. При нарізанні зубчастих коліс методом обкатування різальний інструмент і заготовку також можна розглядати як зубчасту передачу. Однак в процесі нарізання заклинювання не виникає тому, що інструмент зрізає частину профілю зуба, що йому мішає. В результаті отримуємо підріз зубів колеса /рис.5.13/

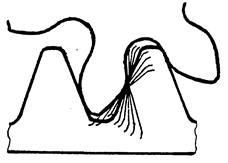Підрізування зубів

Рис. 5.13

Підрізування зовсім не бажане тому, що при цьому видаляється деяка частина активного профілю зуба і це призводить до зменшення коефіцієнта і опору згину, а також збільшення питомих тисків отже, збільшення спрацювання зубів.

Питання про граничне число зубів, яке можна призначити для шестерні, дуже важливе, бо з цим зв’язана зміна габаритів усього механізму, а значить, і збільшення передаточних відношень.

Основною умовою, що обмежує можливість зменшення числа зубів на шестерні, є відсутність підрізування.

Визначимо найменше число зубів Z_min на меншому колесі, при якому відсутнє підрізування.

Для нормального зубчастого зачеплення, у якого кут зачеплення α_w = 20⁰ і коефіцієнт висоти зуба h_a^* = 1,0, найменше число зубів колеса /приведено без виводу/ Z_min = 17.

5.15 Виправлення /корегування/ зубчастих коліс.

Граничне мінімальне число зубів в нормальних евольвентних колесах / α_w = 20⁰ і h_a^* = 1,0/ Z_min = 17 надто велике. Це число можна зменшити, збільшивши кут зачеплення α_w і зменшивши висоту головки зубця h_a = 0,8m.

Для того, щоб передача була особливо компактною, можна відступити від норм стандарту і застосувати такі індивідуальні геометричні умови зачеплення, які дозволяли б здійснити передачу з мінімальними числами зубців і забезпечити при цьому нормальну роботу коліс.

Зубчасті колеса, що відхиляються від норми, мають загальну назву виправлених, або коригованих, зубчастих коліс.

Виправлені колеса широко застосовуються в сучасному машинобудуванні в усіх тих випадках, коли умова замінюваності коліс є неістотною і на перший план висовується умова компактності передачі. Таким чином, виправлені колеса – це парні колеса.

Нарізування зубчастих коліс методом обкатування дає можливість дуже просто замінювати окремі параметри зубчастого колеса і виготовляти не тільки нормальні, а й кореговані зубчасті колеса з іншими раціональнішими параметрами.

Розрахунки та методи виготовлення таких коліс викладені в [1,2,3,4,5].

Змістовий модуль 3. Динамічний аналіз механізмів.

Тема 6. Сили, що діють в механізмах.

6.1Загальні відомості. Основні задачі.

При розгляді кінематичного аналізу механізмів, ми вважали, що закон руху ведучих /вхідних/ ланок заданий. Рух ведених /вихідних/ ланок вивчався в залежності від заданого закону руху ведучих ланок. При цьому сили, які діють на ланку механізму, і сили, що виникають при його русі, нами не враховувалися. Таким чином, при кінематичному аналізі, дослідження руху механізмів ведеться з врахуванням тільки структури механізмів і геометричних співвідношень між розмірами їх ланок.

Динаміка механізмів і машин вивчає рух ланок з врахуванням сил, які визивають цей рух.

Основні задачі динамічного аналізу механізмів:

а) Вивчення впливу зовнішніх сил на ланки механізму і їх елементи, на кінематичні пари і нерухомі опори і визначення способу зменшення динамічних навантажень, які виникають при рухові механізму;

б) Вивчення режиму руху механізму під дією заданих сил і визначення способів, які забезпечують задані режими руху механізму.

Перша задача має назву силового, або кінетостатичного аналізу механізмів, а друга задача - динаміки механізмів.

Усі сили, що діють в механізмах, поділяються на:

1) рушійні сили F_p;

2) сили виробничого /корисного/ опору F_ко;

3) сили тяжіння ланок F_g /гравітаційні сили/;

4) сили тертя та інших невиробничих опорів F_f;

5) реакції зв’язків F_R;

6) сили інерції F_і ;

Сила – це дія навколишнього середовища на тіло, яка прагне змінити його стан спокою, або руху.

Величина сили – це міра механічної взаємодії двох тіл.

Рушійні сили F_p створюються двигунами, які здійснюють перетворення якогось виду енергії /теплової, електричної, гідравлічної/ у механічну роботу. Ці сили намагаються прискорити рух ланок механізму. Елементарна робота dA_p, що здійснюється рушійною силою на елементарному переміщенні dS, завжди додатна:

dA_p= F_pdScos(F_p^V). /6.1/

Отже, рушійна сила збільшує кінетичну енергію машин. В двигуні внутрішнього згоряння рушійна сила створюється в результаті тиску газу, що розширюється, на поршень. В електродвигуні момент рушійних сил виникає в результаті взаємодії між струмом і обмотці ротора і магнітним полем.

Сили виробничого /корисного/ опору F_ко – це сили, для переборювання яких призначена машина /сили опору різання в металообробних верстатах, опору, що виникає при стисканні повітря у компресорах та ін. /.

Сили виробничих опорів з напрямком швидкості точок їх прикладання утворюють тупий кут, або кут, що дорівнює 180⁰. Елементарна робота dA_ko, що здійснюється силою F_ко на елементарному переміщенні dS, від’ємна:

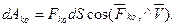- /6.2/

Сила F_ко зменшує кінетичну енергію машин.

Робота A_g сил тяжіння F_g ланок, що визначаються матеріалом та конструкцією ланок, на деякому переміщенні h його центра ваги, що відлічується по вертикалі:

/6.3/

Ця робота буває додатна і від’ємна.

До сил невиробничих опорів належать сили опору повітряного чи рідинного середовища переміщенню ланок і сили тертя F_f в кінематичних парах машин. Сили опору і сили тертя виконують від’ємну роботу. Сили тертя являють собою дотичні складові реакції зв’язків у кінематичних парах.

6.2 Механічні характеристики машин.

Механічною характеристикою двигуна, або робочої машини називають

залежність силового параметра від одного чи кількох кінематичних параметрів і часу.

При доборі двигуна до робочої машини для узгодження оптимального значення кутових швидкостей треба, щоб механічна характеристика двигуна відповідала характеристиці робочої машини. Щоб зменшити габарити та масу агрегату, треба застосовувати швидкохідні двигуни, бо потужність двигуна N дорівнює

N=M_pω, /6.4/

де M_p - момент рушійних сил, ω - кутова швидкість.

У більшості машинних агрегатів безпосереднє з'єднання двигуна з робочою машиною здійснити неможливо. Тому для збільшення величини крутного моменту і відповідного зменшення кутової швидкості між дви­гуном і робочою машиною встановлюють редуктор.

Залежно від типу двигуна чи робочої машини механічні характеристики бувають більш-менш складними. Розглянемо механічні характерис­тики деяких машин.

На рис 6.2 показані механічні характеристики електродвигунів постійного струму: а - з паралельним збудженням; б - з послідовним збудженням.

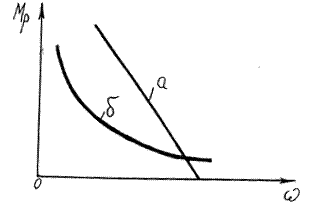Механічні характеристики електродвигунів постійного струму

а - з паралельним збудженням; б - з послідовним збудженням

Рис.6.1

На рис.6.2 показано механічну характеристику асинхронного еле­ктродвигуна трифазного струму.

Механічна характеристика цього двигуна складається з двох час­тин: перша - висхідна, нестійка частина розташована ліворуч М_мах; друга - низхідна, стійка частина розташована праворуч М_мах, ця частина являється робочою. При деякому значенні кутової швидкості ω, що відповідає номінальному моменту М_н, двигуна і номінальній швидкості ω_н, двигун розвиває максимальну потужність. Кутова швид­кість ω_с, при якій М_р= 0, називається синхронною і з цією швидкістю ротор обертається під час холостого ходу. Точка а діаграми визначає положення максимального перекидного моменту М_мах міні­мально допустимої кутової швидкості ω_min робочої частини характе­ристики, а т.О визначає початковий пусковий момент Мп при нульо­вій кутовій швидкості ротора. Умови роботи електродвигунів при низь­ких швидкостях обертання значно погіршуються.

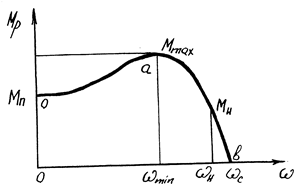Механічна характеристика асинхронного електродвигуна

Рис 6.2

Механічна характеристика двигуна внутрішнього згоряння показана на рис.6.4 двома кривими, що виражають залежність моменту М, який розвивається на головному валу, і потужності N від швидкості ω.

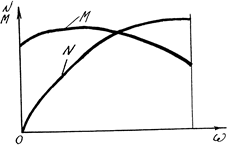Механічна характеристика двигуна внутрішнього згорання

Рис.6.3

6.4. Режими руху механізмів.

Механізм являє собою механічну систему з двосторонніми не залеж­ними від часу зв'язками, що рухається під дією сил. Тому при розв'я­занні деяких питань динаміки механізмів з одним ступенем вільності можна визначити закон зміни кінетичної енергії. Цей закон форму­люється так: приріст кінетичної енергії механізму на кінцевому його переміщенні дорівнює алгебраїчній сумі робіт усіх заданих сил і реакцій зв'язків на відповідних переміщеннях точок їх прикладання

T – T₀ = ΣA, /6.5/

де 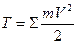- кінетична енергія механізму в довільному положенні;

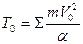- кінетична енергія механізму в початковому положенні; ΣА-алгебраїчна сума робіт усіх сил і моментів, прикладених до механіз­му.

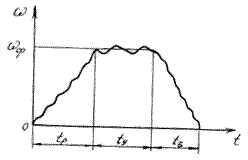
За характером зміни кінетичної енергії повний цикл роботи машинного агрегату в загальному випадку складається з трьох частин: розгону /пуску/, усталеного руху і вибігу /зупинки/ /рис.6.4/.

Час розгону t_p характеризується збільшенням швидкості ведучої ланки від нуля до номінального значення, а це можливо за умови, як­що робота А_р рушійних сил більша, ніж робота А_оп усіх сил опору

А_р> А_оп. /6.6/

Режими руху

Рис 6.4

Час зупинки характеризується зменшенням швидкості ведучої ланки від номінального значення до нуля, тоді

А_р < А_оп. /6.7/

Час розгону і час зупинки машини не повинен бути тривалим. Час усталеного руху t_у найтриваліший, при цьому русі

А_р = А_оп. /6.8/

Протягом цього часу виконується корисна робота, для здійснення якої і призначений агрегат.

Робота А_оп усіх сил опору складається із суми робіт А_ко сил корисного /виробничого/ опору і робіт A_f сил тертя та інших не­виробничих опорів:

А_оп = А_ко+ A_f. /6.9/

16. 4. Види тертя. Тертя ковзання сухих тіл.

Загальний опір, що виникає в місцях дотику двох тіл, які пере­міщуються одне відносно одного, називається силою тертя. Тертя - це складне явище, для пояснення якого створені дві гіпотези: механічна і молекулярна.

За сучасною гіпотезою, що має змішанний характер, процес тертя при ковзанні поверхонь є результатом не лише механічної взаємодії поверхонь, але і результатом дії молекулярних сил.

В загальному тертя розрізняють таких видів:

а/ чисте - сухе;

б/ граничне, якщо поверхні розділяє шар мастила завтовшки не більше ніж 0,1 Мкм;

в/ рідинне, поверхні певністю розділені шаром мастила;

г/ напівсухе - одночасно сухе і граничне;

д/ напіврідинне - одночасно рідинне і граничне.

По видам рухів розрізняють:

а/ тертя ковзання;

б/ тертя кочення.

Сила F_f сухого тертя, яка виникає при відносному ковзанні од­ного тіла відносно іншого, пропорційна силі F_N нормального тиску і визначається із рівняння Амонтона-Кулона

F_f = f F_N, /6.10/

де f - коефіцієнт тертя ковзання.

Коефіцієнт тертя f залежить від матеріалів поверхонь що труть­ся, їх стану та обробки, мащення та інших факторів.

Не дивлячись на це, коефіцієнт тертя f для конкретних матеріалів приймається сталим.

Сила тертя завжди напрямлена в сторону, протилежну швидкості відносного ковзання тіла.

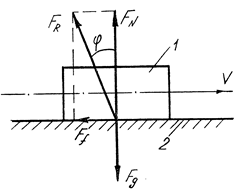
Повна реакція F_R ланки 2 на ланку 1 визначається додаванням нормальної реакції F_N і сили тертя F_f /рис. 6.5/.

Визначення кута тертя

Рис. 6.5

Повна реакція F_R відхилена від нормальної реакції F_N на кут φ, який називається кутом тертя ковзання

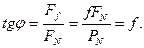/6.11/

Таким чином, коефіцієнт тертя дорівнює тангенсу кута тертя.

6.5. Тертя на похилій площині.

Знайдемо рушійну силу F_Р, необхідну для рівномірного перемі­щення тіла 1, на яке діє гравітаційна сила F_g /сила тяжіння/, вгору на похилій площині 2, якщо коефіцієнт тертя ковзання рівний f. Похила площина і рушійна сила F_Р складають з горизонталлю кути, відповідно α і β /рис.6.6,а/.

При рівномірному переміщенні тіла 1 на похилій площині 2 вгору на нього діють: рушійна сила F_Р, сила тяжіння F_g, нормальна реакція F_N та сила тертя F_f.

Знайдемо повну реакцію F_R шляхом додавання нормальної реакції F_N та сили тертя F_f. Реакція F_R складає з нормаллю до площини кут тертя φ.

Складемо векторне рівняння всіх сил, що діють на тіло 1:

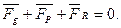/6.12/

Тіло на похилій площині

а - переміщення тіла вгору; б - план сил

Рис. 6. 6

Побудуємо план сил /рис. 6. 6, б/. Отримаємо замкнутий силовий трикутник із відповідними кутами при вершинах. На основі теореми синусів можна записати:

/6.13/

Звідси знайдемо рушійну силу

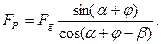/16.14/

Якщо сила F_Р горизонтальна, кут β=0, то рівняння /16.14/ прийме вигляд:

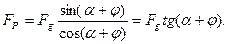/16.15/

Розглянемо випадок, коли тіло 1 рухається рівномірно донизу /рис.6.7,а/.

В цьому разі побудова відрізняється від попередньої тим, що сила тертя F_f напрямлена вверх, а повна реакція F_R відхиляється на кут тертя φ, не ліворуч від нормалі /рис. 6.6, а/, а праворуч від неї /рис.6.7,а/.

Для цього випадку досить у формулах /6.14/ і /6.15/ замінити кут φ на –φ. Тоді будемо мати:

/6.16/

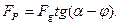/6.17/

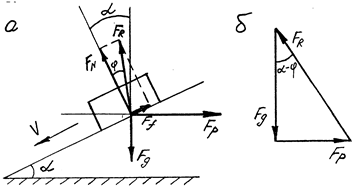Тіло на похилій площині

а - переміщення тіла донизу; б - план сил

Рис. 6. 7

Рівняння /6.17/ також випливає із /рис. 6.7, б/.

При відсутності тертя /кут φ = 0/ рівняння /6.7/ набере вигляду:

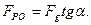/6.18/

6.6. Тертя в клинчастому і циліндричному жолобі. Тертя в гвинтовій пврі

Цей матеріал викладено в [1,2,3].

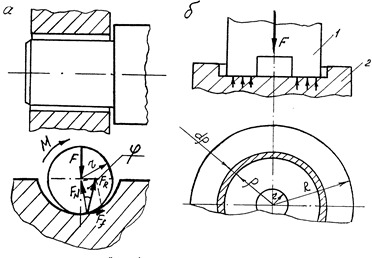
6.7. Тертя в обертальних парах: цапфі, п'яті.

Вали можуть передавати на опори як радіальні, так і осьові зу­силля.

Розглянемо випадок, коли вал передає на опору радіальне зусил­ля, тобто визначимо момент тертя в цапфі /рис.6.8,а/.

Обертальні кінематичні пари

Рис.6.8

Момент тертя в цапфі визначається за формулою:

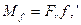/6.19/

f `= 1,27f - приведений коефіцієнт тертя в припрацьованій цапфі.

Визначимо момент тертя в п'яті /вал передає на опору осьове зу­силля/, /рис.6.8,б/.

В цьому випадку на поверхні стикання п'яті 1 і підп'ятника 2 виникає сила тертя вертіння, яка підкоряється закону Амонтона-Кулона.

На рис.6.8,б показана кільцева п'ята, яка має опорну поверхню у вигляді кільця шириною R - r.

Величина питомого тиску Р на одиницю площі постійна і рівна

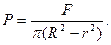/6.20/

Виділимо на опорній поверхні п”яті кільце радіусом ρ і шириною d ρ

Елементарний момент тертя dМf на цій площі

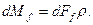/6.21/

Елементарна сила тертя рівна

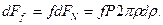/6.22/

Рівняння /6.21/ з врахуванням /6.4/ прийме вигляд:

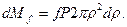/6.23/

Проінтегруємо рівняння /6.23/ в границях від r до R

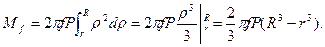/6.24/

Підставимо в рівняння /6.24/ значення Р Із /6.20/, отримаємо:

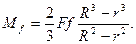/6.25/

Якщо п'ята суцільна, то r = 0 і рівняння /6.25/ прийме вигляд:

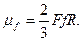/6.26/

6.8. Тертя гнучкої ланки по нерухомому барабану.

Розглянемо випадок, коли за допомогою гнучкої ланки /паса/, пе­рекинутої через нерухомий циліндричний барабан, рушійною силою F_P піднімається вантаж, на який діє сила тяжіння F_g /рис. 6. 9, а/. Нехай коефіцієнт тертя між гнучкою ланкою і барабаном f. Визна­чимо рушійну силу F_P, необхідну для рівномірного переміщення вантажу вверх. Для надання гнучкій ланці рівномірного руху, необ­хідно перебороти силу тертя, яка виникає між гнучкою ланкою і ба­рабаном. Позначимо кут в рад. обхвата пасом барабана α.

Виділимо на поверхні барабана елемент dS. Цей елемент буде знаходитися в рівновазі під дією нерівних сил натягу F_T і нормальної реакції барабана F_N і елементарної сили тертя dF_f /рис. 6. 9, б/. Очевидно, що

/6.27/

З іншого боку маємо:

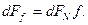/6.28/

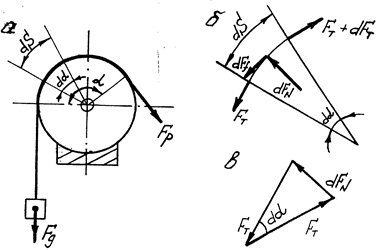Гнучка ланка на барабані

а - барабан - гнучка ланка; б - елемент барабана; в - план сил

Рис. 6. 9

Порівнюючи /6.27 І /6.28/, знаходимо:

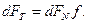/6.29/

Отже, елементарна сила тертя зрівноважується елементарною си­лою натягу в dF_T, а тому їх можна відкинути.

Побудуємо план сил /рис. 6. 9, в/. Складемо векторне рівняння сил:

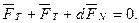/6.30/

Із трикутника сил маємо:

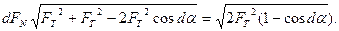/6.31/

Відомо, що 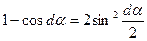і при малих кутах α, 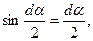тоді рівняння /6.31/ прийме вид:

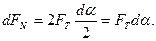/6.32/

Враховуючи значення dF_N із /6.29/ знайдемо елементарну силу натягу dF_T із /6. 29/

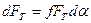або 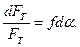/6.33/

Проінтегруємо рівняння /6.33/:

/6.34/

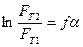, або 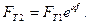/6.35/

Оскільки F_T2 = F_P, а F_T1 = F_g то рівняння /6.35/ остаточно прийме вигляд:

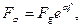/6.36/

Ця залежність була отримана вперше Леонардом Ейлером в 1765 р.

Для клинового паса:

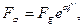/6.37/

де f^’ - приведений коефіцієнт тертя 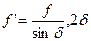кут профілю паса.

6.9. Тертя кочення у вищих кінематичних парах.

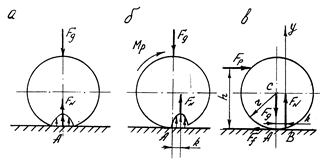
Якщо циліндр знаходиться в стані спокою на горизонтальній пло­щині і на нього діє сила тяжіння F_g, то крива розподілу напру­жень в зоні контакту колеса з площиною буде симетрична і реакція буде проходити через т.А /рис. 6. З, а/.

Прикладемо до колеса рушійний момент М_ρ /рис,6. 10, б/, або го­ризонтальну рушійну силу F_ρ на висоті h /рис. 6. 10, в/, які спричинять рівномірне кочення колеса /циліндра/. В цих випадках кри­ва розподілу напружень буде не симетрична. При цьому реакція F_N площини зміститься назустріч руху на величину R, яку будемо на­зивати плечем сили тертя кочення, або коефіцієнтом тертя кочення. Величина R вимірюється в мм. При рівномірному коченні колеса можна скласти наступні рівняння рівноваги:

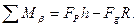; /6.38/

Із рівнянь /6.38/ маємо:

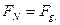
/6.39/

де F_Ph = М_Р - момент рушійних сил, F _g К = М_f - момент сил тертя кочення.

При рівномірному коченні момент рушійних сил дорівнює моменту сил тертя 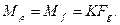/6.40/

Циліндр на горизонтальній площині

а - у стані спокою; 6 - навантажений рушійним моментом; в - навантажений рушійною силою

Рис.6. 10

Рушійна сила знаходиться із /6.39/

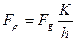. /6.41/

В залежності від висоти h можливі три випадки:

1) чисте ковзання буде проходити, якщо

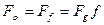i 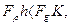/6.42/

звідки знаходимо:

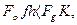або /6.43/

2) чисте кочення можливе, якщо

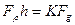і 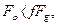/6.44/

звідки знаходимо:

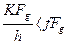, або 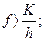/6.45/

З) одночасне кочення і ковзання буде, якщо

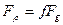і 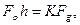/6.46/

звідки знаходимо:

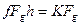або 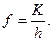/6.47/

6.10. Переміщення вантажу на катках. Переміщення вантажу на візку

Ці задачі викладені в [1,2,3].

6.11. Визначення сил інерції ланок плоских механізмів.

При вивченні цього матеріалу слід звернутися до [1,2,4].

6.12. Умова статичної визначеності кінематичного ланцюга.

Рух ланок механізму здійснюється під дією прикладених до них зовніш-ніх сил. Сили взаємодії ланок, що виникають в місцях їх доти­ку, називаються реакціями в кінематичних парах.

Вважатимемо, що тиск в кінематичних парах розподіляється рівно­мірно по їх елементах, які приймаємо за абсолютно гладенькі, тобто силами тертя нехтуємо. Напрям рівнодійної тиску у парі про­ходить по спільній нормалі до дотичних поверхонь. Таким чином, результуюча тиску в обертальній парі проходить через центр шарніра /рис.6.11,а/. Величина і лінія дії цієї рівнодійної не відомі. У поступальній парі /рис. 6.11, б/ результуюча реакція напрямлена пер­пендикулярно до напрямних, але величина і точка прикладання її та­кож не відомі.

Таким чином, для визначення реакції в кожній із нижчих кінема­тичних пар 5 класу необхідно знайти дві невідомі.

Реакція в вищій кінематичній парі 4 класу проходить по спіль­ній нормалі до дотичних поверхонь /рис.6.11,в/. Невідома тільки її величина.

Для кожної ланки кінематичного ланцюга можна скласти три рів­няння рівноваги, тоді для п ланок можна скласти З п рівнянь рівноваги. Число невідомих, які потрібно визначити, буде: для пар V класу 2P₅, а для пар ІV класу Р₄ .

Статично визначеним буде кінематичний ланцюг, у якого число рів­нянь дорівнює числу невідомих, тобто:

3n = 2p₅+p₄ /6.48/

Вищі кінематичні пари ІV класу можна замінити нижчими парами V кла­су /див. рис.3.6/, тоді матимемо:

3n = 2p_5. /6.49/

Зусилля в кінематичних парах

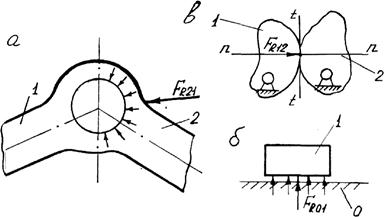
а і б - нижчі кінематичні пари: обертальна і поступальна; в - вища

кінематична пара

Рис. 6. 11

Звідки 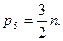/6.50/

n	2	4	6
P5	3	6	9

Поєднання числа ланок і числа кінематичних пар V класу в рів­нянні /6.50/, аналогічне їх поєднанню для груп Ассура /рівняння 1.6/

Таким чином, всі групи Ассура є статично визначеними, тобто чис­ло рівнянь, які можна скласти для групи Ассура, дорівнює числу невідомих.

6.13. Кінетостатика груп Ассура П класу П порядку.

Кінетостатичний розрахунок механізмів проводиться в послідовності, оберненій утворенню механізмів, тобто розпочинається з останньої приєднаної групи Ассура і закінчується механізмом І класу. Отже, кінетостатичний розрахунок механізмів зводиться до розрахунку окремих груп Ассура і механізму І класу.

Силовий розрахунок будемо проводити методом планів сил. Вважа­тимемо, що всі зовнішні сили, прикладені до ланки, а також сили інерції і моменти пар сил інерції замінені однією узагальненою силою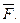

Механізми, утворені із груп Ассура І виду, застосовуються, нап­риклад, у верстатах, підйомних механізмах кранів і ін.

Накреслимо в певному масштабі групу Ассура_І виду /рис. 6. 12, а/. Нехай до ланки 2 прикладено узагальнену силу 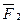, а до ланки 3 - узагальнену силу . Лінію дії, величину і точки прикладання обох сил задано. Дію від'єднаних ланок механізму замінимо реакціями в кі­нематичних парах F_Ri. Ці реакції невідомі як за величиною, так і за нап­рямом.

Розкладемо кожну невідому, прикладену в центрі шарніра, на дві складові: нормальну 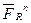- напрямлену вздовж відповідної ланки і тангенціальну - напрямлену перпендикулярно до цієї ж ланки. Тоді, згідно принципу Даламбера, група буде в стані рівноваги, і до неї можна застосовувати рівняння статики.

Кожну ланку окремо також можна розглядати в стані рівноваги, так як дію однієї ланки на другу можна замінити реакцією в середній кі­нематичній парі.

Кінетостатика групи Ассура П кл., П пор., І виду

а - група Ассура І виду; б - план сил

Рис. 6.12

Визначимо тангенціальні складові реакції, розглянувши рівновагу окремо кожної ланки. Візьмемо суму моментів всіх сил відносно т .В для другої ланки:

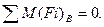/6.51/

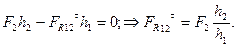/6.52/

Візьмемо суму моментів всіх сил відносно т.В для третьої ланки:

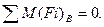/6.53/

/6.54/

Складемо векторне рівняння суми всіх сил, що діють на групу Ас­сура:

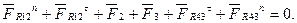/6.55/

Побудуємо план сил в масштабі /рис. 6.12,б/:

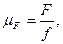/6.56/

де 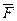- дійсне значення сили в Н; f - відрізок на плані сил в мм, що зображає дійне значення сили.

Вибираємо довільну точку P_F - полюс план сил і з неї, в виб­раному масштабі, розпочинаємо побудову плана сил. Відкладемо вектор, що зображає реакцію - 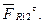Затим, згідно векторного рівняння /6.55/ відкладаємо послідовно вектори всіх сил, згідно їх величини і напряму. Проводимо лінії дії нормальних реакцій 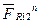і 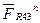до їх взаємного перетину. Повні реакці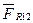ї і 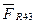отримаємо до­даванням відповідних нормальних і тангенціальних складових.

Визначимо реакцію в середній кінематичній парі. Для цього розг­лянемо рівновагу однієї ланки, наприклад, другої. Складемо векторне рівняння:

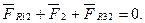/6.57/

На плані сил знайдемо реакцію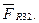Для цього з'єднаємо кінець вектора 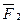і із початком вектора 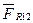. Дійсні значення реакцій знайдемо множенням відповідного відрізка, що зображає цю реакцію на масштаб плана сил, наприклад: 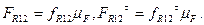/6.58/

6.14. Кінетостатика механізму І класу.

Накреслимо в масштабі механізм І классу /рис. 6. 13, а/. Прикладемо в

центрі мас S₁ силу тяжіння 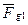та силу інерції 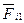. Дію від'єднаної ланки 2 замінимо реакцією 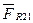, яка дорівнює 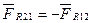. До ланки 1 в т. А прикладемо зрівноважувальну силу 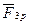і визначи­мо її. Візьмемо суму моментів всіх сил відносно т. О:

/6.59/

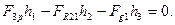/6.60/

Із рівняння /6.60/ знаходимо:

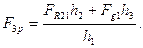/6.61/

Визначимо реакцію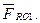Складемо векторне рівняння сил, що діють на механізм І класу:

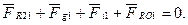/6.62/

Побудуємо план сил в масштабі μ_F /рис.6.13,б/, згідно вектор­ного рівняння /6.62/.

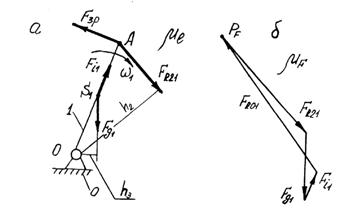Кінетостатика механізму І класу

а - механізм І класу; б - план сил

Рис. 6.13

Кінець вектора сполучимо з початком вектора Отри­маний вектор і буде зображати реакцію .

Таким чином, кінетостатичне дослідження механізмів дозволяє виз­начити реакції у всіх кінематичних парах та зрівноважувальну силу, або зрівноважувальний момент:

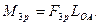/6.63/

6.15. Визначення коефіцієнту корисної дії при послідовному з'єд­нанні механізмів.

Нехай маємо п послідовно з'єднаних механізмів /рис.6.14 /.

Прикладом послідовного з'єднання механізмів може бути теплосило­ва установка. Роботою рушійних сил тут є енергія палива; роботою сил виробни-чого опору - енергія, що виділяється головним валом двигуна; роботою сил

Послідовне з'єднання механізмів

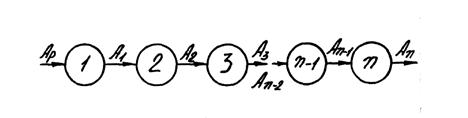Рис.6.14

невиробничих опорів - послідовні втрати у топці, котлі, паропроводах, у двигуні і т.д.

Іншими прикладами послідовного з'єднання механізмів можуть бути: привод стрічкового конвеєра /електродвигун, муфта, зубчасті передачі редуктора, підшипники, гнучка передача, стрічковий конвеєр/; привод автомобіля /двигун внутрішнього згорання, муфта, коробка передач, кардан, диференціальний механізм, ведучі колеса/.

Позначимо А₁ роботу сил корисного опору на вихідному валу пер­шого механізму і роботу сил рушійних на вхідному валу другого меха­нізму, А₂ роботу сил корисного опору на вихідному валу другого ме­ханізму і роботу сил рушійних на вхідному валу третього механізму і т.д. Таким чином, ККД усієї машини: 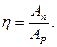/6.64/

Окремі ККД кожного механізму будуть:

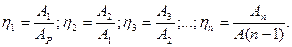/6.65/

Запишемо тотожність:

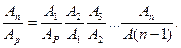/6.66/

Підставимо в тотожність /6.66/ значення множників із /6.65/, отри­маємо:

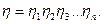/6.67/

ККД послідовного з'єднання механізмів дорівнює добутку ККД окремих механізмів.

Тема 7. Рух та регулювання руху механізмів

7.1. Основні відомості.

Вивчаючи рух механізму, ми досі припускали, що вхідна /ведуча/ ланка обертається із сталою кутовою швидкістю / ω₁ = соnst /. Для здійснення такого руху потрібне цілком певне співвідношення між сила­ми, що діють на механізм. Взагалі неможливо встановити таке співвід­ношення між силами, що діють на механізм, яке б забезпечило заданий закон його руху.

У більшості випадків сили корисного опору залежать від положення ланок, до яких вони прикладені. Наприклад, сила опору стиску повітря в циліндрі компресора залежить від його кутової швидкості. У ряді ви­падків сили корисних опорів залежать від швидкості точок їх прикла­дання, а іноді від часу. Наприклад, момент опору пропелера залежить від його кутової швидкості, а зусилля перемішування тіста залежить від часу перебування тіста у місильній машині. Сила опору переміщен­ню транспортного засобу /автомобіля/ залежить не тільки від маси ван­тажу, але і від швидкості та профілю шляхопроводу.

Визначення закону руху механізму, що перебуває під дією прикла­дених до його ланок заданих сил, і є задачею динамічного аналізу. Для механізму, що має один ступінь вільності, цю задачу можна вважати розв'язаною, коли буде встановлено закон руху однієї ланки. За таку ланку, звичайно, вибирають ведучий вал робочої машини або ведений вал двигуна. До цієї ланки, що приймається за ланку зведення, доцільно звести всі сили й моменти пар сил, що прикладені до механізму. При цьому необхідно, щоб потужність, яку розвиває замінююча сила, дорів­нювала сумі потужностей, що розвивають всі сили, прикладені до ланок механізму. Цю замінюючу силу називатимемо зведеною силою F_зв.

Маси всіх ланок зручно замінити деякою умовною масою, зосередже­ною в точці зведення. При цьому необхідно, щоб кінетична енергія зве­деної маси в даному положенні дорівнювала сумі кінетичних енергій усіх ланок механізму. Тоді замість розглядання всього комплексу сил, що діють на ланки механізму, можна розглянути сили, що діють лише на одну ланку - ланку зведення, наприклад кривошип О₁А /рис.7.1/, що перебуватиме під дією зведеної сили F_зв або зведеного моменту M_зв /у загальному випадку змінних/ і матиме зведену масу т_зв / у загальному випадку також змінну/, зосереджену ніби в точці А зведення.

Якщо ланка зведення робить обертальний рух, то всі діючі сили і моменти доцільно замінити однією зведеною парою сил з моментом М_зв а всі маси і динамічні моменти інерції ланок замінити зведеним дина­мічним моментом інерції І_зв, наданим ланці зведення О₁А.

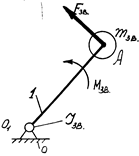Вхідна ланка /ланка зведення/

Рис.7.1.

Отже, у цьому випадку задача полягає у визначенні закону руху однієї ланки, що перебуває під дією зведеного моменту і має зведений динамічний момент інерції І_зв. Закон руху всіх інших ланок механіз­му можна визначити методом планів швидкостей та прискорень, або ме­тодом кінематичних діаграм.

7.2. Зведені сили і моменти.

Зведеного силою /моментом/ називається сила /момент/, що замінює дію всіх сил і моментів в механізмі із умови рівності миттєвих по­тужностей зведеної сили /моменту/ і всіх сил і моментів, що зводяться.

Сила /момент/, що дорівнює за величиною зведеній силі /моменту/ і протилежно їй напрямлена, називається зрівноважувальною силою /мо­ментом/.

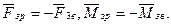/7.1/

Точка, до якої прикладена зведена сила, називається точкою зве­дення, а ланка, до якої зводяться всі сили і моменти, називається ланкою зведення.

Нехай до механізму /рис.7.2,а/ прикладені сила F₃ і момент M₂.

В загальному випадку, на основі визначення зведеної сили /момен­ту/ можна записати: 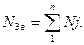/7.2/

Кривошипно – повзун ний механізм

а - кінематична схема; б - повернутий план швидкостей

Рис.7.2.

Миттєві потужності визначаються за відомими формулами:

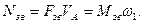/7.3/

/7.4/

Із рівнянь /7.3/ та /7.4/ маємо:

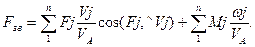/7.5/

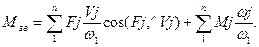/7.6/

Для конкретного механізму /рис.7.2,а/ із діючою силою F₃ і моментом M₂ зведена сила дорівнює:

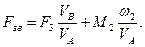/7.7/

Зведений момент буде:

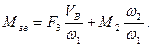/7.8/

Лінійні швидкості точок і кутові швидкості ланок можна визначити, по­будувавши повернутий план швидкостей /рис.7.2,б/.

7.3. Теорема М.Є. Жуковського.

Знайти зведену силу, або зведений момент можна також, користую­чись методом М.Є.Жуковського.

Теорема М.Є.Жуковського читається так. Якщо механізм під дією систе-ми прикладених до нього сил перебуває в рівновазі, то і повернутий на 90° план швидкостей механізму, навантажений тими ж силами, прикладеними в однойменних точках плану, також перебуватиме в рівно­вазі.

План швидкостей розглядається як жорсткий важіль з опорою в по­люсі плану. Теорему Жуковського можна також застосувати до системи, яка не пере-буває в рівновазі. Для цього потрібно крім діючих сил прикласти до системи ще й сили інерції, а моменти пар сил інерції замінити парами сил інерції. Система цих прикладених сил умовно пе­ребуватиме в рівновазі і до них можна застосу-вати теорему Жуковсько­го. Для доведення теореми скористаємось принципом можливих переміщень /принцип Даламбера/. Сума можливих робіт заданих сил Fj на елементар­них переміщеннях δSj точок їх прикладання дорівнює нулю. Математич­ний вираз принципу можливих переміщень має вигляд:

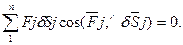/7.9/

Поділимо /7.9/ на dt, дістанемо:

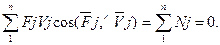/7.10/

де Fj - задані сили; Vj - швидкості точок прикладання сил Fj; Vjcos()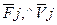

проекції швидкостей тих самих точок на лінії дії сил Fj; Nj - потужності, що розвивають сили Fj.

Нехай в точці j ланки АВ прикладена сила Fj /рис.7.З,а/. Пере­несемо цю силу паралельно їй самій в однойменну точку j / повернутого на 90° плану швидкостей ланки /рис.7.З,б/.

Із повернутого плану швидкостей потужність Nj сили можна визначити так:

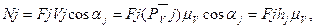/7.11/

де h_j - перпендикуляр, опущений із полюса P_V плану швидкостей на лі­нію дії сили F_i; α _j - кут між вектором швидкості 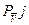і плечем h_j.

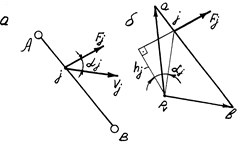До теореми М.Є.Жуковського

а - ланка механізму; б - повернутий план швидкостей

Рис.7.3.

Застосуємо рівняння /7.11/ для всіх сил

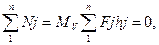/7.12/

що і є доведенням теореми.

7.4. Зведена маса і зведений динамічний момент інерції механізму.

Зведеною масою, /динамічним моментом інерції/ механізму, нази­вається така умовна маса /динамічний момент інерції/, яка будучи зосередженою в точці зведення має кінетичну енергію, що дорівнює сумі кінетичних енергій всіх ланок механізму.

Отже, кінетична енергія зведеної маси т_зв, зосередженої в точці А ланки

зведення /рис.7.4/ 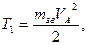або кінетична енергія зведеного динамічного моменту інерції І_зв.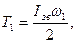

має дорівнювати сумі Tj кінетичних енергій усіх ланок механізму, тобт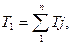о: або 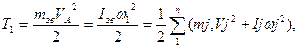/7.13/

Звідки дістаємо:

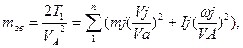/7.14/

/7.15/

У формулах /7.14/ і /7.15/ m_j і I_j - це відповідно маса j - i ланки та її динамічний момент інерції відносно осі, що проходить че­рез центр маси перпендикулярно площині руху, V_j - швидкість центра маси ланки; ω_j - кутова швидкість ланки; V_A - швидкість точки зведен­ня А; ω₁ - кутова швидкість ланки зведення.

7.5. Рівняння руху машини.

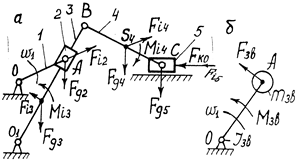
Виконавши зведення сил і мас, будь-який механізм з однією ступін­ню вільності /важільний, зубчастий, кулачковий і ін./ /рис.7.4,а/, яким би складним він не був і скільки б сил на нього не діяло, можна замінити динамічною моделлю /рис.7.4.б/.

Основою для складання рівняння руху механізму чи машини з однією ступінню вільності є теорема про зміну кінетичної енергії: Т-Т_о =ΣА,

де Т і Т_о - кінетична енергія механізму відповідно в довільному і по­чатковому положенні; ΣА - сума робіт всіх сил /рушійних і опору/.

Рівняння руху в формі рівняння кінетичної енергії буде мати виг­ляд:

/7.16/

де і 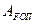робота зведених до ланки зведення сил рушійних і сил опору; ,

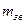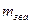і V, V₀ - зведені маси і швидкості точки зведення відповідно в довільному і початковому положенні.

Механізм стругального верстату

а - кінематична схема; б - динамічна модель

Рис.7.4.

Якщо ланка зведення здійснює обертальний рух навколо нерухомої осі, то рівняння руху прийме вигляд:

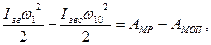/7.17/

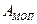де і - робота зведених до ланки зведення моментів рушійних і опору; ,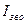і 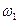, 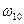- зведені динамічні моменти інерції ланок і кутова швидкість ланки зведення відповідно в довільному і початко­вому положенні.

7.6. Нерівномірність руху механізмів.

Рівномірність руху частин механізму є істотно важливою умовою най-вигіднішого його використання. Розрізняють два типи коливання швидкостей механізму: періодичне і неперіодичне, що зумовлено голов­ним чином зміною навантаження механізму.

У ротаційних двигунах /електродвигуни/ робочий процес відбуваєть­ся не циклічно, а безперервно і при усталеному русі характеризується сталістю рушійного моменту; отже, у цих двигунах періодичних коливань швидкості не буде і головна ланка при усталеному русі обертатиметься рівномірно.

У поршневих двигунах, в основі яких лежить кривошипно-повзунний механізм, орган, що сприймає роботу рушійних сил /поршень/, робить зворотно-поступальні рухи. Це ускладнює регулювання кутової швидкості обертання головного вала двигуна. В таких двигунах рушійна сила і си­ла корисного опору являються змінними величинами, незалежними одна від одної. Усталений рух механізму супроводжується періодичними змі­нами швидкості обертання головного вала. Така нерівномірність нази­вається періодичною. Великі періодичні коливання швидкості недопусти­мі, бо вони спричиняють у кінематичних парах додаткові динамічні зу­силля, які знижують надійність роботи механізму та його загальний коефіцієнт корисної дії. Задача про сталість швидкості обертання по­лягає в тому, щоб неминучі періодичні коливання швидкості усталеного руху довести до деяких, наперед заданих значень. Отже, питання зво­диться до задачі регулювання коливань швидкості обертання головного вала при усталеному русі. Це регулювання здійснюється за допомогою додаткової маси - маховика /колеса з великим динамічним моментом інер­ції/, який встановлюють на одному з валів механізму.

Дія маховика полягає в тому, що при перевищенні роботи рушійних сил над роботою сил опору, маховик сприймає на себе надлишок кінетич­ної енергії механізму, завдяки своєму великому моменту інерції не дає швидкості надмірно зростати; коли ж робота сил опору перевищує робо­ту рушійних сил, маховик віддає нагромаджену кінетичну енергію, про­тидіючи зменшенню швидкості.

Крім періодичних коливань, у механізмі можливі коливання швидкос­ті, що не мають певного циклу, так звані неперіодичні коливання. Ці коливання можуть виникати при раптовій зміні навантаження, включення в механізм додаткових мас тощо. Неперіодичні коливання регулюють за допомогою спеціальних механізмів, які називаються регуляторами.

7.7. Середня швидкість руху. Коефіцієнт нерівномірності руху.

При проектуванні та розрахунку механізмів середнє значення куто­вої швидкості вхідної ланки /головного валу/ за один цикл усталеного руху завжди задається на основі загальних міркувань про роботу меха­нізму в зв'язку з його робочим процесом.

Розглянемо усталений рух, при якому через деякі проміжки часу па­раметр руху буде повторюватися /рис.7.5/.

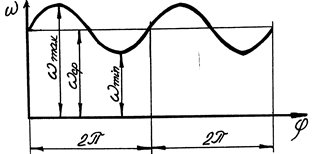Зміна кутової швидкості вхідної ланки

Рис.7.5.

Цей проміжок часу назвемо циклом періодичного руху. При визначенні середньої кутової швидкості ω_СР користуються наб­лиженою формулою:

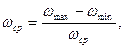/7.18/

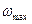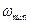де і - відповідно максимальна і мінімальна кутові швидкос­ті вхідної ланки.

Середня швидкість ω_СР береться рівною номінальній кутовій швид­кості, тобто кутовій швидкості, яка проставляється у паспорті двигуна механізму, або машини. При регулюванні руху механізмів треба наперед знати, в яких межах допускається робочим процесом механізму зміна ку­тової швидкості ω_СР вхідної /головної/ ланки. Ці межі установлюються з досвіду. Нерівномірність руху механізму характеризується відношен­ням абсолютної нерівномірності руху механізму до його середньої швид­кості;

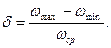/7.19/

Величина 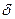називається коефіцієнтом нерівномірності руху механізму. Найсуворіші вимоги щодо рівномірності руху повинні задовольняти дви­гуни, які надають рух електричним генераторам змінного струму. Для них 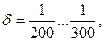для металообробних верстатів 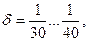для двигу­нів внутрішнього згоряння <

Дата добавления: 2014-01-04