Виведення рівнянь Нав’є – Стокса

Виділимо в потоці рідини, що рухається по каналу, елементарний паралелепіпед з ребрами dx, dy, dz (рис.2.1.2). На цей елемент діють три сили: сила тяжіння, сила тиску і сила тертя.

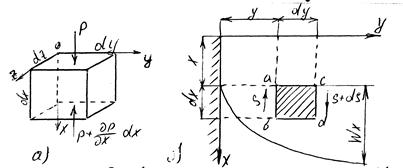
Рис. 2.1.2. До виведення диференційного рівняння руху незріджуючої в’язкої рідини

Сила тяжіння може бути визначена добутком густини рідини на об’єм елемента:

G = gp dx dy dz,

де р – густина рідини;

g – прискорення вільного падіння.

Силу тиску можна знайти шляхом наступних міркувань. Гідростатичний тиск в даному випадку змінюється вздовж вертикальної вісі. Нехай на верхній грані значення тиску р, тоді на верхню грань діє сила 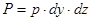. Тиск біля нижньої грані елемента рівний 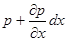тому сила тиску рівна

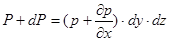
Результуюча цих сил і буде силою тиску, що діє на елемент:

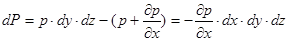(2.1.1)

Силу тертя виразимо виходячи з припущень про плоско-паралельний рух потоку. В цьому випадку локальні швидкості руху частинки в потоці 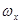(рис.2.1.2.б) змінюються лише в напрямку вісі у, а тертя виникає лише на бічних гранях аb і сd. Біля грані ab швидкість руху рідини меньше, ніж швидкість руху виділеного елементу, тому сила тертя напрямлена проти руху. Якщо силу тертя, віднесену до одиниці поверхні, позначити через S, то сила тертя, що діє на грань ab, рівна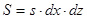

Біля грані cd швидкість руху частинок більша, за швидкість руху елемента, і силу тертя, напрям котрої співпадає з напрямом руху елемента, можна виразити як

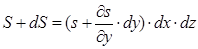
Результуюча зазначених сил і є сила тертя, що діє на елемент потоку рідини:

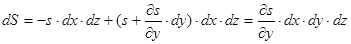(2.1.2).

Згідно закону Ньютона-Петрова,

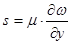
Тому силу тертя можна виразити як:

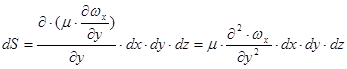(2.1.3)

На основі другого закону механіки (рівнодіюча сил рівна масі, помноженій на прискорення) для даного випадку запишемо:

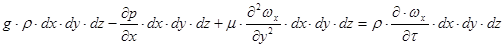(2.1.4)

або

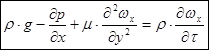(2.1.5)

це диференційне рівняння для рівномірного усталого руху незріджуючої в’язкої рідини.

Для випадку трьохмірного неусталого руху незріджуючої в’язкої рідини (р=const) отримують більш складні рівняння, але структура їх зберігається:

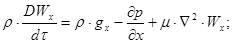
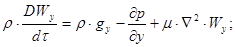
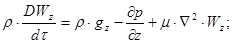(2.1.6)

Рівняння (2.1.6) руху незріджуючої в”язкої рідини називають рівняннями Нав”є-Стокса.

Де похідні 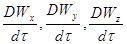в лівій частині р.івняння (2.1.6) являють собою повні похідні швидкості по часу:

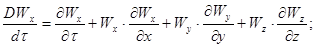
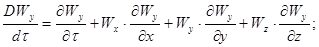
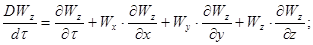(2.1.7)

Перші члени доданків правих частин рівнянь (2.1.7) визначають локальні зміни складових швидкості у часі. Три останні доданки правих частин рівнянь враховують переміщення елементу рідини з однієї точки простору в іншу.

Велечини 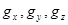- складові рівняння вільного падіння в напрямку окремих вісів координат.

Символом 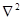(набла) позначений оператор Лапласа, являє собою суму других похідних:

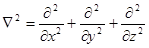(2.1.8)

Отримання чисел подібності з диференційного рівняння для рівномірного усталого руху незріджуючої рідини.

Всі члени рівняння (2.1.5) мають розмірність сили, що віднесення до об”єму. Для приведення рівняння до безрозмірного виду розділимо всі його члени на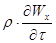, в результаті отримаємо:

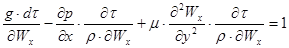(2.1.9)

Кожен доданок лівої частини рівняння (2.1.9) безрорзмірний. З них можна отримати числа подібності. Для цього викреслимо символи диференціювання і символи, що характеризують напрям (заміна х і у не орієнтованим в певному напрямку лінійним розміром l).

1). З першого доданку отримаємо число Фруда, яке характеризує відношення сил тяжіння до інерційних сил:

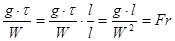(2.1.10)

2). З другого доданку отримаємо число Ейлера, що характеризує відношення сил тиску в потоці до інерційних сил:

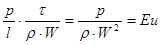(2.1.11)

3). Третій доданок дає величину, зворотню числу Рейноль деа:

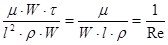(2.1.12)

Числа Re,Eu,Fr можна отримати з рівнянь Нав”є-Стокса (2.1.6). Крім цього з цих рівнянь додатково можна отримати число гомохронності, що враховує неусталений характер руху в подібних потоках:

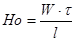(2.1.13)

Рівняння подібності, що описує рух потоку фільтруючої рідини, наводять в наступному вигляді:

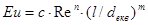(2.1.14)

Дата добавления: 2014-01-04