Основні властивості плану швидкостей та прискорень

1) Усі точки механізму, швидкості (прискорення) яких дорівнюють нулю, на плані швидкостей (прискорень) знаходяться в полюсі.

2) Усі вектори, що виходять з полюса плану швидкостей (прискорень), є векторами абсолютних швидкостей (прискорень).

3) Усі вектори плану, що з’єднують кінці векторів абсолютних швидкостей (прискорень), є векторами відносних швидкостей (прискорень). Замірявши відповідні відрізки (в мм) на плані швидкостей (прискорень) та помноживши їх на масштаб , знаходимо дійсні (за модулем) значення швидкостей (прискорень).

4) Для плану швидкостей та прискорень дійсна теорема подібності.

Приклад 2. На рис. 2.11, а показана кінематична схема механізму поперечно-стругального верстата. В його склад входять початкова ланка 1 та дві групи Ассура ІІ класу: група, що складається з ланок 2 та 3 третього виду, та група ІІ(4,5) п’ятого виду.

Необхідно побудувати плани швидкостей і прискорень для положення визначеного кутом 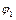. Кутова швидкість кривошипа 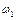= const.

Знаходимо швидкість т. В, яка належить ланці 1, м/с.

Від полюса 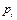плану швидкостей відкладаємо відрізок 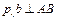, який зображує вектор швидкості v_B (Рис. 2.11, б). При цьому масштаб плану швидкостей дорівнює

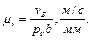
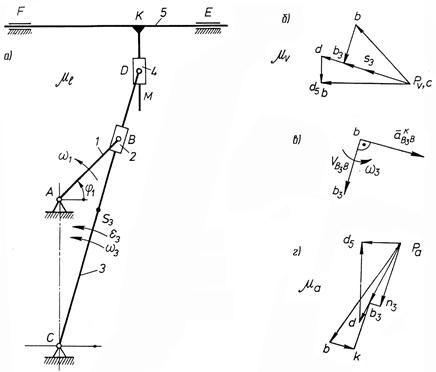
Рис. 2.11

Переходимо до визначення швидкостей точок ланок першої структурної групи. Відомі швидкості точок В і С, які належать зовнішнім кінематичним парам групи: швидкість т.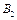, яка належить ланці 2 (повзуну), дорівнює швидкості т. В кривошипа (першої ланки), тобто . Невідома швидкість точки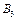, яка належить ланці 3, кулісi і в даному положенні механізму, співпадає з т. В, що лежить на кривошипі (повзуні). Для її визначення записуємо систему векторних рівнянь

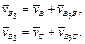
За першим рівнянням з точки b, кінця вектора (швидкості т. В) проводимо пряму, паралельну до ланки CD (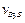є швидкість відносного поступального руху повзуна 2 по напрямній 3; напрямлена вздовж неї). За другим рівнянням з точки с, яка співпадає з полюсом p_V, (v_c = 0), проводимо пряму, перпендикулярну до ВС. На перетині цих прямих одержуємо точку b₃. Вектор 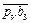зображує швидкість 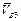точки 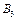, що належить кулісі.

Використовуючи теорему подібності, знаходимо положення точки D на плані швидкостей

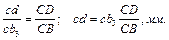
Відкладаємо відрізок сd на продовженні відрізка cb₃ , знаходимо точку d.

Швидкість т. D₅, яка належить ланці 5, визначаємо з рівняння

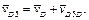
Усі точки ланки 5 рухаються вздовж напрямної EF, тобто абсолютна швидкість т. D₅ паралельна напрямній, 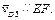Таким чином, з полюса p_v проводимо пряму, паралельну до EF, а з т. d – пряму, паралельну до КМ. На перетині одержуємо т. d₅. Сполучаємо її з полюсом p_V.

Положення т. S₃ знаходимо за теоремою подібності з пропорції

.

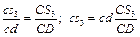Вимірявши відповідні відрізки в мм, множимо їх на масштаб 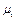і одержуємо величини шуканих швидкостей

.

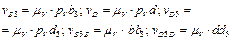Кутову швидкість ланки 3 визначимо за формулою 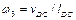. Напрямок цієї швидкості знаходимо за допомогою вектора швидкості 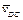. Умовно переносимо цей вектор у т. D механізму та спостерігаємо за умовним обертанням ланки 3 відносно точки С проти руху стрілки годинника. Таким чином, 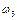напрямлена у той же бік.

Побудова плану прискорень. Прискорення т. В, яка належить ланці 1 кривошипу, визначається за формулою

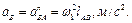
Від полюса p_a (рис. 2.11, г) відкладаємо відрізок p_ab паралельно до ланки АВ (у напрямку від т. В до т. А), який зображує прискорення (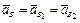). Масштаб плану прискорень при цьому .

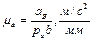Визначаємо прискорення т.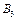, що належить ланці 3,

У першому рівнянні 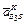, - коріолісове прискорення, яке з’явилось у результаті складання відносного поступального руху повзуна 2 по напрямній 3 зі швидкістю 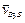та переносного обертального руху цієї напрямної зі швидкістю 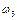. Модуль цього прискорення визначається за формулою

.

Щоб знайти напрямок вектора 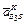, необхідно повернути вектор відносної швидкості 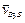на кут 90⁰ в напрямку переносної кутової швидкості 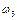(рис. 2.11, в). Прискорення 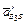є прискоренням відносного поступального руху повзуна 2 по напрямній 3 і напрямлене вздовж ланки CD. Величина (модуль) його невідома. Нормальне прискорення 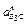визначається за формулою 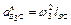, воно напрямлене від точки В до точки С паралельно до ланки СВ. Дотичне прискорення 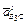напрямлене перпендикулярно до ланки ВС. Визначаємо відрізки bk i p_an₃, які зображують прискорення на плані

.

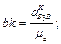
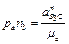Відкладаємо від точки b плану прискорень відрізок bk, а від полюса p_a відрізок p_an₃. З точки k проводимо лінію, паралельну до ВС, а з точки n₃ - лінію, перпендикулярну ВС до їх перетину між собою. Точку перетину b₃ з’єднуємо з полюсом і одержуємо відрізок p_ab₃, який зображує прискорення 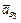точки 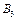. Для визначення положення точки D на плані прискорень складаємо рівняння, використовуючи теорему подібності,

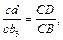звідки .

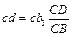Щоб знайти прискорення точки 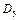, яка належить ланці 5, записуємо векторне рівняння

,

.

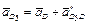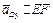Прискорення 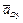напрямлене вздовж напрямної EF, а відносне (релятивне) прискорення - вздовж КМ. З полюса р_a проводимо лінію, паралельну до EF, а з точки d – лінію, паралельну до КМ. На перетині цих ліній одержуємо точку 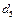. Величини знайдених прискорень дорівнюють

;

.

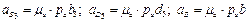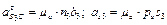Модуль кутового прискорення 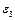ланки 3 знайдемо за формулою

.

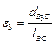Напрямок 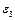знаходимо з допомогою дотичного прискорення 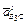. Переносимо вектор 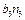, що зображає 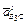.на плані, у точку В механізму і бачимо, що він вказує на умовне обертання ланки 3 навколо точки С проти руху стрілки годинника.

Дата добавления: 2014-01-04