Кінематичне дослідження механізмів аналітичними методами

Широке розповсюдження ЕОМ з різноманітним програмним забезпеченням сприяє все більшому застосуванню аналітичних методів кінематичного дослідження. З великої кількості праць з аналітичного розв’язку задач кінематики, якщо розглядати лише загальні методи, які можна застосувати для будь-яких механізмів, виділяють два їх різновиди: метод замкнених векторних контурів, розроблений В.А.Зінов’євим, та метод перетворення координат (матричний метод), запропонований Ю.Ф.Морошкіним.

Аналітичне розв’язування задач кінематики просторових механізмів рекомендують виконувати методом перетворення координат. Застосування цього методу дає змогу визначати кінематичні параметри звичайними алгебричними методами із застосуванням матриць. Перевага матричної форми запису полягає, головним чином, у застосуванні формул множення матриць.

Аналітичне дослідження плоских механізмів зручніше виконувати методом замкнених векторних контурів.

Метод замкнених векторних контурів. Метод полягає у тому, що кінематичні параметри визначаються у вигляді аналітичних залежностей, що одержують, якщо представити схему механізму замкненими векторними контурами, утвореними ланками цього механізму. Вихідними даними є структурна схема механізму, розміри ланок та залежності узагальнених координат механізму від часу. Якщо останні не задано, то рівняння записують як функції узагальнених координат, тобто визначають кінематичні передатні функції.

Суть методу замкнених векторних контурів полягає в наступному:

- ланки механізму зображають у вигляді векторів, які утворюють на схемі механізму один або декілька замкнених векторних контурів (відповідно до кількості груп Ассура);

- складають векторні рівняння замкненості кожного контуру;

- вибирають прямокутну систему координат та проектують рівняння замкнутості контурів на осі вибраної системи координат.

В результаті отримують аналітичні залежності положення ланок від узагальнених координат механізму та його розмірів, тобто функцію положень ланок механізму;

- диференціюють двічі за часом рівняння замкненості контурів у проекціях на осі x, y та отримують, відповідно, систему рівнянь для визначення швидкостей та прискорень ланок механізму. Якщо диференціюють по узагальненій координаті – отримують, відповідно, рівняння для визначення аналогів швидкостей та прискорень.

- визначають координати, проекції швидкостей та прискорень характерних точок механізму. Визначають модулі швидкостей та прискорень цих точок.

Деякі рекомендації щодо застосування методу замкнених векторних контурів:

- напрямок векторів слід вибирати так, щоб вони вказували послідовність побудови схеми механізму. Спочатку у вигляді вектора зображають початкову ланку механізму. Початок цього вектора – нерухома точка (центр шарніра). Вектори, що зображають ланки в групах Ассура, рекомендують напрямляти до внутрішньої кінематичної пари. Напрямок векторів на нерухомій ланці вибирають довільно;

- записуючи умови замкненості векторних контурів, треба враховувати знаки векторів. Для цього користуються правилом обходу: обходячи кожний векторний контур схеми у довільно вибраному напрямі, векторам, напрям яких збігається з напрямом обходу, присвоюють знак плюс і, навпаки, для векторів, що мають напрям проти напряму обходу, присвоюють знак мінус;

- прямокутну систему координат зв’язують зі стояком. За початок відліку можна прийняти центр шарніру, що з’єднує початкову ланку зі стояком. Якщо у механізмі є нерухома напрямна для повзуна, то одну з осей координат доцільно проводити паралельно до цієї напрямної.

Зазначимо, якщо механізм утворює декілька замкнених векторних контурів, то послідовність їх розгляду визначається послідовністю приєднання.

б

Методику одержання розрахункових залежностей розглянемо на прикладі кривошипно-повзунного механізму двоступінчастого двоциліндрового повітряного компресора, структурна схема якого зображена на рис. 2.12, а. Задані розміри всіх ланок та частота обертання кривошипа 1. Необхідно визначити усі кінематичні параметри ланок та їх характерних точок (центрів мас) S₂, S₄.

Представимо схему механізму у вигляді двох замкнутих векторних контурів: OABO та OCDO (рис. 2.12, б). У кожен контур входить структурна група Ассура другого класу: ІІ(2, 3) та ІІ(4, 5). Ланки механізму зобразимо у вигляді векторів 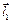,,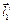 , , 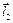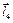положення повзунів 3, 5 визначатиметься векторами , .

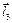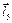Складемо векторні рівняння замкнутості кожного контура

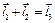, (2.6)

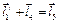. (2.7)

Рівняння (2.6), (2.7) спроектуємо на осі вибраної прямокутної системи координат xOy (за початок відліку якої прийнято центр шарніра О, а вісь Оу направлено вздовж напрямної повзунів) та запишемо рівняння проекцій.

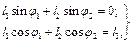(2.8)

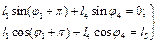, (2.9)

де 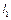, , 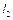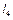– відповідно довжини ланок 1, 2, 4; 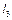, 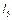– відповідно відстані між центром шарніра О та центрами шарнірів B, D повзунів; 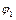- узагальнена координата механізму (кут повороту кривошипа); 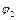, 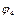– відповідно кути повороту ланок 2, 4.

Відлік кутів 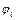, які визначають положення ланок, проводимо від додатного напрямку осі Оу за рухом годинникової стрілки (в напрямку обертання кривошипа). Отже, для визначення величини та напряму кута повертаємо вісь Оу за годинниковою стрілкою доти, доки стрілка осі Оy не зіллється зі стрілкою вектора. Це й буде позитивним напрямом кута.

Розв’язуючи системи (2.8), (2.9) відносно невідомих 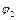, 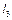та 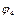, , 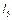отримаємо аналітичні залежності положень ланок 2, 3, 4, 5 від узагальненої координати, тобто функції положень ланок. Так для першого контура, з першого рівняння системи (2.8) одержимо:

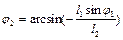, (2.10)

а з другого рівняння (2.8) врахувавши (2.10), отримаємо

.

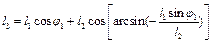Для другого контура всі викладки аналогічні.

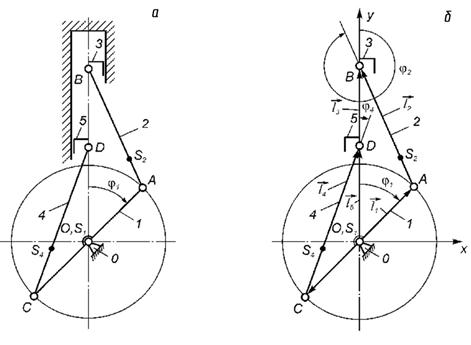
Рис. 2.12

Диференціюючи систему (2.8) за часом,

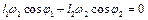, (2.11)

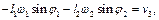(2.12)

з (2.11) отримаємо вираз для кутової швидкості шатуна 2, а з (2.12) – лінійної швидкості повзуна 3

,

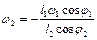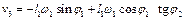
У випадку, коли закон руху початкової ланки невідомий, визначають аналоги швидкостей та прискорень, продиференціювавши системи (2.8) і (2.9) за узагальненою координатою.

Для визначення прискорень двічі диференціюємо за часом систему (2.8), що приводить до рівнянь

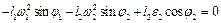, (2.13)

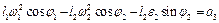. (2.14)

З (2.13) визначаємо кутове прискорення шатуна 2

.

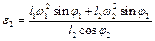Підставивши значення 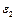в рівняння (2.14), можна визначити лінійне прискорення повзуна 3.

Координати будь-якої характерної точки механізму, її швидкість та прискорення визначають, використовуючи рівняння проекцій даної точки на осі координат. Наприклад, для т. S₂ будемо мати

,

.

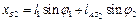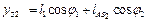Модулі швидкостей та прискорень цієї точки знаходяться за відомими формулами

, .

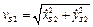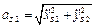Наведені результати аналітичного дослідження зручні для програмування та реалізації на ЕОМ. Для складніших механізмів ІІ класу з декількома групами Ассура метод замкнутих векторних контурів може призвести до громіздких математичних виразів. Реалізація відповідних алгоритмів на ЕОМ призводить до складних програм. З метою спрощення методики дослідження механізмів ІІ класу рекомендується погруповий метод кінематичного дослідження. Враховуючи, що будь-який механізм отримується послідовним приєднанням до початкового механізму груп Ассура, доцільно аналітичне дослідження механізмів виконувати за структурними групами. При цьому рух ланок для кожної групи розглядається окремо, з врахуванням кінематичних характеристик її зовнішніх кінематичних пар, якими вона приєднується до механізму. Створені уніфіковані блоки (підпрограми) для початкових механізмів та груп Ассура. Такий метод зводить дослідження механізмів до розгляду окремих структурних груп, методика кінематичного дослідження яких не залежить від механізму, у який вони входять.

Для кінематичного дослідження механізмів високих класів рекомендують метод замкнутих векторних контурів.

Питання для самоконтролю

1. Що вивчає кінематика?

2. Назвіть основні задачі кінематики.

3. Назвіть методи кінематичного дослідження механізмів.

4. Що називається планом механізму?

5. Що таке масштаб?

6. Послідовність побудови планів механізму.

7. Як визначаються початкові положення основних важільних механізмів?

8. Що таке шатунні криві?

9. Що називається кутом робочого ходу?

10. Яка сутність методу обернення рухів?

11. Дайте визначення функцій положень механізму.

12. Що таке перша та друга передатні функції механізму?

13. Запишіть формули, які відображають зв’язок між передатними функціями механізму та його кінематичними характеристиками.

14. Переваги аналітичних методів кінематичного дослідження.

15. Суть методу замкнених векторних контурів.

16. Послідовність графічного диференціювання.

17. Послідовність графічного інтегрування.

18. Масштаби при графічному диференціюванні.

19. Теорема подібності.

ГЛАВА 3. ВСТУП У ДИНАМІЧНИЙ АНАЛІЗ МЕХАНІЗМІВ ТА МАШИН. СИЛОВИЙ РОЗРАХУНОК МЕХАНІЗМІВ

У кінематиці дослідження руху ведеться тільки з врахуванням будови механізмів та геометричних співвідношень між розмірами ланок. Передбачається, що рух вхідних ланок відомий. Рух вихідних ланок вивчається в залежності від заданого руху вхідних ланок. За цих умов сили, які діють на ланки механізму, не враховуються.

Динаміка вивчає дійсний рух механізмів з урахуванням усіх факторів, що на нього впливають. Динамікою називається розділ механіки, у якому вивчається рух матеріальних тіл під дією сил. Розрізняють дві основні задачі динаміки:

- визначення сил, які діють на ланки механізмів за заданим законом руху, та встановлення способів зменшення динамічних навантажень, що виникають при русі механізмів;

- визначення дійсного закону руху механізмів під дією прикладених до нього сил та встановлення способів забезпечення заданих режимів руху механізму.

Перша задача має назву силового аналізу механізмів, а друга – динаміки механізмів.

У динаміку входять і ряд інших задач, що мають важливе технічне значення: тертя у кінематичних парах; механічний коефіцієнт корисної дії механізмів; теорія коливань в механізмах та віброзахист машин і т. ін.

Крім цього у динаміці можна виділити два класи задач – аналіз механізмів і машин та синтез механізмів і машин за заданими динамічними умовами.

Дата добавления: 2014-01-04