Кодирование положительных и отрицательных чисел

Системы счисления

q=8	h=2	q=16	h=2	q=16	h=2
				A(10)
				B(11)
				C(12)
				D(13)
				E(14)
				F(15)

Перевод целых чисел из одной системы счисления в другую с основанием q можно осуществить путем последовательного деления исходного числа и промежуточных частных на основание q. При этом остаток от первого деления дает младшую цифру числа в новой системе счисления, а остатки от деления промежуточных частных - последующие цифры. Деление заканчивается как только частное будет меньше основания q. Это частное дает старшую цифру числа в новой системе счисления. Особенность способа деления на основание заключается в том, что все вычисления выполняются в исходной системе счисления, в этой же системе получаются и цифры искомого числа. Способ деления на основание можно рекомендовать при переводе чисел из десятичной системы в систему с любым другим основанием.

Перевод правильной дроби из одной системы счисления в другую с основанием q осуществляется путем последовательного умножения исходной дроби и промежуточных произведений на основание q. При этом целая часть от первого произведения дает старшую цифру искомой дроби, а целые части от умножения последующих дробных частей произведения последующие цифры. Умножение продолжается до получения требуемого числа цифр после запятой. При умножении q представляется в системе счисления исходного числа.

В ЭВМ выполнение операции вычитания (или алгебраического сложения) чисел сводится к арифметическому сложению их кодов, что приводит к упрощению структуры арифметического блока. Это достигается путем представления чисел в прямом [Х]пр, обратном [Х]обр и дополнительном [Х]доп кодах.

Прямой код. Пусть имеется число X в виде правильной дроби ұ0,g1,g2..., gn, тода правило образования прямого кода правильной дроби имеет вид:

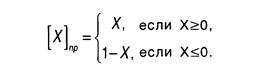
Согласно этому правилу запись прямого кода положительного числа имеет следующий вид: [X+]пр=0,g1,g2..., gn, а прямой код отрицательного числа [Х-]пр=0,g1,g2..., gn.

Прямой код целого числа образуется по следующему правилу:

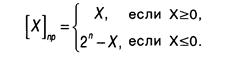
где n - количество разрядов для представления чисел. В ЭВМ прямой код используется для выполнения операций умножения и деления, для хранения операндов в различных запоминающих устройствах, при вводе и выводе информации.

Алгебраическое сложение отрицательных чисел выполняется в дополнительном или обратном кодах. Обратный код отрицательной дроби имеет вид: [X]обp=1,d1,d2,...dn, где

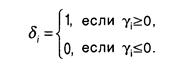
т.е. для перехода от прямого кода отрицательного числа к обратному необходимо в знаковый разряд записать единицу, а в цифровых разрядах единицы заменить нулями, нули - единицами. По этим же правилам осуществляется переход к обратному коду целого отрицательного числа.

Дополнительный код. Для получения дополнительного кода отрицательного числа в знаковый разряд кода записывается единица, в цифровых разрядах единицы заменяются нулями, нули - единицами, и к младшему разряду прибавляется единица. Таким образом, дополнительный код отрицательного числа может быть получен из обратного путем прибавления 1 к младшему разряду. Изображения положительных чисел в дополнительном и обратном кодах совпадают с изображениями в прямом коде.

В различных кодах нуль представляется следующим образом:

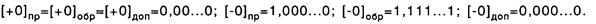
Операции алгебраического сложения и вычитания двоичных чисел в машинах осуществляются в обратном и дополнительном кодах. Использование этих кодов позволяет заменить определение разности вычислением суммы. Для обнаружения переполнения по результату операции анализируются переносы из старшего разряда в знаковый и из знакового разряда.

При сложении кодов двух чисел с одинаковыми знаками может возникнуть переполнение. Полученный результат при этом превосходит по абсолютной величине максимально допустимое значение для данного формата чисел. В ЭВМ переполне­ние разрядной сетки фиксируется, и вырабатывается сигнал " Переполнение". При с ложении двух положительных чисел имеет место переполнение, если образован перенос из старшего значащего разряда в знаковый, а из знакового разряда пере­нос отсутствует.

При сложении двух отрицательных чисел, если имеет место переполнение, то образуется перенос из знакового разряда, а перенос в знаковый разряд отсутствует.

Умножение двоичных чисел с произвольным сочетанием знаков удобно выполнять, если сомножители заданы в прямом коде. В этом случае независимо от знаков модуль произведения определяется перемножением модуля множимого на все разряды множителя и последующего сложения полученных частичных произведений, а знак произведения определяется как сумма по модулю 2 знаков обоих сомножителей. Процесс получения произведения сводится к умножению множимого X на каждую цифру у i множителя У:

Частичные произведения П i =Х·У i, получаемые при этом, последовательно складываются. Сумма всех частичных произведений образует полное произведение.

В ЭВМ умножение чисел обычно сводится к выполнению операций сложения и сдвига. При умножении двух n-разрядных чисел результат произведения представляется 2 n-разрядным числом. Умножение чисел можно производить, начиная с младших разрядов, либо со старших разрядов множителя. В процессе умножения можно сдвигать либо сумму частичных произведений (СЧП), либо множимое. Комбинируя эти возможности получают четыре основных метода умножения.

1. Умножение младшими разрядами вперед множителя со сдвигом СЧП вправо.

2. Умножение младшими разрядами вперед множителя со сдвигом множимого влево при неподвижной СЧП.

3. Умножение старшими разрядами вперед множителя со сдвигом СЧП влево и неподвижном множимом.

4. Умножение старшими разрядами вперед множителя при сдвиге вправо множимого при неподвижной СЧП.

Техническая реализация первого метода умножения проще, чем реализация других методов.

Деление чисел с фиксированной запятой
При делении по заданному делимому А и делителю В определяется частное C=A/B. Очевидно, что В¹0, так как деление на нуль не имеет смысла. Вследствие того, что в цифровой машине с фиксированной запятой наиболее часто применяется такое представление числа, когда оно меньше единицы [Х]<1, то на делимое, делитель и частное накладываются дополнительные ограничения: ½Аô<1, çВô<1, çСô<1. Из последнего неравенства следует, что должно быть çАô<çВô.

Если результат деления из-за соотношений величины делимого и делителя получается больше единицы, то операция не выполняется. При этом вырабатывается сигнал "Переполнение" или "Ошибка". При делении чисел в прямых кодах в операции участвуют модули делимого и делителя. Знак частного (как и при умножении) может быть определен как сумма по модулю 2 знаков делимого и делителя, а модуль частного как частное от деления модуля делимого на модуль делителя.

Процесс деления состоит из последовательности операций вычитания делителя вначале от делимого, а затем из образующихся остатков, предварительно сдвинутых на каждом шаге деления влево на один разряд. Если очередной остаток положительный, то в разряд частного записывается единица; если остаток отрицательный - нуль. Процесс вычитания повторяется, количество повторений определяется разрядностью частного.

В зависимости от того, какие действия производятся после получения очередного отрицательного остатка для определения следующего значения разряда частного, различают методы деления с восстановлением и без восстановления остатков.

При первом методе предыдущий остаток восстанавливается путем суммирования делителя çУô к отрицательному остатку ½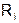ô, т.е. (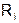+У). Для получения очередного разряда частного восстановленный остаток сдвигается на один разряд влево (т.е. удваивается), и из него вычитается делитель: 2·(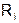+У)-У.

При втором методе отрицательный остаток сдвигается на один разряд влево, и к нему прибавляется делитель: 2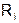+У, т.к. 2(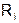+У)-У=2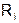+У.

Сравнивая эти методы нетрудно убедиться, что первый метод требует больше операций сложения и вычитания. Поэтому в современных ЭВМ используется метод деления без восстановления. При выполнении операции деления результат получается одинаковым, если сдвигать остатки деления влево при неподвижном делителе, либо сдвигать делитель вправо при неподвижном остатке от деления. Таким образом, возможны две схемы выполнения операции деления:

1) деление без восстановления остатков со сдвигом делителя при неподвижном остатке от деления;

2) деление без восстановления остатков со сдвигом остатков влево при неподвижном делителе.

Для реализации первого варианта требуются 2n - разрядный регистр делителя со сдвигом вправо и 2n - разрядный сумматор, (n+1) - разрядный регистр частного со сдвигом влево и схема управления.

Для реализации второго варианта потребуется n - разрядный регистр делителя, (n+1) разрядный регистр частного со сдвигом влево, n - разрядный сумматор со сдвигом влево и схема управления.

Анализ вариантов схем деления показывает, что второй вариант является более экономичным по сравнению с первым.

Дата добавления: 2014-01-04