
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Логические основы ЦУ
|
|
|
|
Деление двоичных чисел в прямом коде.
При делении чисел в прямом коде знак произведения определяется путем сложения по модулю два значений цифр в знаковых разрядах.
Частное определяется путем деления модуля делимого X на модуль делителя У. При этом должно соблюдаться условие çХô<çУô. В противном случае возникает переполнение разрядной сетки ЭВМ, что является недопустимым. Для этого перед выполнением деления с фиксированной запятой производится пробное вычитание делителя из делимого. Если при этом остаток имеет отрицательный знак, то деление возможно, а положительный знак указывает на некорректность деления.
Деление правильных дробей также, как и деление целых чисел, выполняется циклически, причем в каждом цикле определяется цифра частного, начиная со старшей.
Для вычитания из модуля делимого и положительных текущих остатков используется двоичное дополнение кода делителя. При таком способе деления цифры частного определяются по следующему правилу: если знак очередного остатка положительный, то в соответствующий разряд частного заносится единица, если отрицательный - нуль. Если последний остаток получается отрицательным, то при необходимости получения действительного остатка он восстанавливается добавлением к нему делителя, и присваивается знак действительного делимого.
Основная литература: 1 [62-88], 3 [51-82], 3 [67-98]
Дополнительная литература: 5 [23-28], 7 [35-61],7 [111-145], 9 [305-361]
Контрольные вопросы:
1. Назовите основные системы счисления?
2. Какие действия необходимо произвести для сложения чисел?
3. Как преобразовать прямой код двоичных чисел в обратный и дополнительный код?
4. Чем отличается кодировка отрицательных и положительных чисел?
5. Чем отличается сложение чисел с фиксированной и плавающей запятой?
6. Приведите алгоритм умножения чисел с фиксированной запятой?
7. Чем отличается умножение двоичных чисел в прямом и дополнительных кодах?
8. Отметьте осбенности выполнения операции умножения и деления чисел с плавающей запятой от умножения и деления чисел с фиксированной запятой?
9. Назовите основные способы деления и умножения двоичных чисел?
10. Что такое сумма частичных произведений (СЧП)?
Тема лекции 2. Логические основы ЦУ. Булева алгебра. Функции алгебры логики (ФАЛ). Способы задания ФАЛ. Комбинационные схемы. Последовательностные схемы (конечные автоматы).
В результате выполнения арифметических операций получают новое двоичное число. Устройство, реализующее действия над двоичными числами, можно рассматривать как функциональный преобразователь. Если рассматривать отдельные разряды исходных чисел и конечных результатов вычислений в качестве аргументов и функций, то устройство, осуществляющее арифметическое действие имело бы большое количество входов и выходов. Причем на каждый вход поступал бы один разряд исходного числа (0 или 1), а с каждого выхода снимался бы один двоичный разряд результата (0 или 1).
Для анализа и синтеза таких устройств необходимо иметь математический аппарат, позволяющий оперировать с двоичными переменными. Основы такого аппарата были впервые сформированы в середине прошлого века английским математиком Д.Булем. Переменные величины и функции от них, которые могут принимать только два значения 0 или 1, носят название булевских или логических переменных и функций.
Функциями алгебры логики (ФАЛ) называются функции, определенные на наборе двоичных переменных (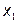 ,
,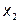 ,...
,... 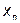 ) и сами принимающие в качестве своих значений либо нуль, либо единицу. Задать ФАЛ - это значит определить ее значение (0 или 1) на каждом возможном наборе значений аргументов. Количество различных наборов аргументов равно количеству различных чисел, которые могут быть изображены с помощью n разрядов, т.е. 2. Так как на каждом наборе аргументов ФАЛ может принимать одно из двух значений, то количество различных ФАЛ от п аргументов конечно и равно
) и сами принимающие в качестве своих значений либо нуль, либо единицу. Задать ФАЛ - это значит определить ее значение (0 или 1) на каждом возможном наборе значений аргументов. Количество различных наборов аргументов равно количеству различных чисел, которые могут быть изображены с помощью n разрядов, т.е. 2. Так как на каждом наборе аргументов ФАЛ может принимать одно из двух значений, то количество различных ФАЛ от п аргументов конечно и равно 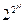 Ниже рассматриваются всевозможные ФАЛ от n аргументов для n=0, 1, 2.
Ниже рассматриваются всевозможные ФАЛ от n аргументов для n=0, 1, 2.
1. n=0. Существуют  =2 различные ФАЛ; f1=0 - константа нуль, f2=1 - константа единица.
=2 различные ФАЛ; f1=0 - константа нуль, f2=1 - константа единица.
2. n=1. Существуют  =4 различные ФАЛ.
=4 различные ФАЛ.
Их можно определить с помощью табл. 2.1 в левой части которой указаны возможные наборы аргументов, а в правой значения ФАЛ на каждом наборе. Такая таблица называется таблицей истинности ФАЛ.
Кроме уже известных ФАЛ f1 и f2 в табл. 2.1. определены еще две ФАЛ: f3=x - функция тождества; f4=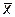 - функция отрицания (читается f равно "не х").
- функция отрицания (читается f равно "не х").
Таблица 2.1
| х | f1 | f2 | f3 | f4 |
3. n=2. Существуют 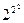 =16 различных ФАЛ, которые задаются их таблицей истинности (табл. 2.7.). Первые шесть ФАЛ табл. 2.2. уже известны: f1 - константа 0; f2 константа 1; f3=
=16 различных ФАЛ, которые задаются их таблицей истинности (табл. 2.7.). Первые шесть ФАЛ табл. 2.2. уже известны: f1 - константа 0; f2 константа 1; f3=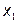 ; f4=
; f4=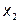 ; f5=
; f5=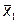 ; f6=
; f6= . Функция f7 называется дизъюнкцией, обозначается f7=
. Функция f7 называется дизъюнкцией, обозначается f7=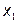 \/
\/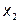 или f7=
или f7=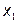 +
+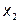 ; дизъюнкция принимает значение 1,если хотя бы один.из аргументов paвен 1.
; дизъюнкция принимает значение 1,если хотя бы один.из аргументов paвен 1.
Таблица 2.2.
| x1 | x2 | f1 | f2 | f3 | f4 | f5 | f6 | f7 | f8 | f9 | f10 | f11 | f12 | f13 | f14 | f15 | f16 |
Функция f8 называется конъюнкцией, обозначается f8=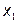 /\
/\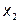 ; конъюнкция принимает значение 1, если оба аргумента равны 1. Функция f8 называется эквивалентностью (равнозначностью) и обозначается f9=
; конъюнкция принимает значение 1, если оба аргумента равны 1. Функция f8 называется эквивалентностью (равнозначностью) и обозначается f9=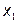 ~
~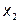 ; принимает значение 1, если аргументы равны. Функция f10 называется сложением по модулю два и обозначается f10=
; принимает значение 1, если аргументы равны. Функция f10 называется сложением по модулю два и обозначается f10=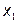 Å
Å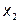 ; принимает значение 1 на тех наборах, где значения аргументов не совпадают. Функция f11 называется импликацией x1 в x2 обозначается f11=
; принимает значение 1 на тех наборах, где значения аргументов не совпадают. Функция f11 называется импликацией x1 в x2 обозначается f11=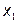 ®
®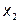 . Функция f12 называется импликацией x2 в х1 и обозначается f12=
. Функция f12 называется импликацией x2 в х1 и обозначается f12=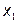 ®
®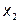 . Функция f13 называется функцией Вебба (стрелка Пирса) и обозначается f13=
. Функция f13 называется функцией Вебба (стрелка Пирса) и обозначается f13=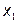 ¯
¯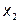 . Функция f14 называется функцией Шеффера и обозначается f11=
. Функция f14 называется функцией Шеффера и обозначается f11=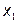 /
/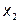 . Функции f15 и f16 специальных названий не имеют.
. Функции f15 и f16 специальных названий не имеют.
Перечисленные 14 ФАЛ называются элементарными и имеют особое значение в алгебре логики. Количество различных ФАЛ с увеличением n растет очень быстро. Уже для n=4 существуют 5536 различных ФАЛ.
Способы задания ФАЛ.
1. Табличный способ. Из определения ФАЛ следует, что всякая функция алгебры логики задается таблицей истинности, определяющей какое значение (0 или 1) принимает данная функция на всех наборах аргументов.
2. Графический способ. Если набору значений аргументов сопоставить точки n-мерного пространства, то произвольная ФАЛ от n аргументов будет определяться двумя непересекающимися множествами вершин n-мерного куба: множеством вершин Т0, где функция принимает значение 0, и множеством вершин Т1, где она равна 1.
3. Аналитический способ. Для перехода от табличного задания ФАЛ к более удобной аналитической записи используются совершенные дизъюнктивные и совершенные конъюнктивные нормальные формы представления ФАЛ (ДСНФ и КСНФ). Любая ФАЛ может быть записана в ДСНФ и КСНФ.
Для получения ДСНФ функции алгебры логики, заданной таблично, необходимо:
1) отметить все наборы аргументов, на которых функция принимает значение 1;
2) выписать конъюнкции аргументов для каждого отмеченного набора. При этом, если аргумент имеет в отмеченном наборе значение 1, он выписывается в соответствующую конъюнкцию без отрицания, в противном случае - с отрицанием;
3) соединить полученные конъюнкции знаком дизъюнкции.
Таблица 2.3
| x1 | x2 | x3 | f(x1x2x3) | x1 | x2 | x3 | f(x1x2x3) |
П р и м е р 2.1. Пусть табл. 3.3. задает некоторую ФАЛ от трех аргументов.
Чтобы получить ДСНФ этой ФАЛ:
1) отмечаются наборы аргументов, где f(x1x2x3)=1;
2) выписываются конъюнкции  Ù
Ù Ù
Ù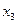 ;
; 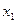 Ù
Ù Ù
Ù ;
;  Ù
Ù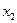 Ù
Ù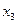 ;
; 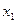 Ù
Ù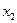 Ù
Ù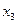 .
.
3) полученные конъюнкции соединяют знаком дизъюнкции: f(x 1,x2,x3)=  Ù
Ù Ù
Ù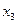 Ú
Ú 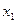 Ù
Ù Ù
Ù Ú
Ú Ù
Ù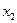 Ù
Ù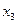 Ú
Ú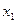 Ù
Ù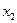 Ù
Ù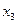 . Полученная аналитическая запись f(x1, x2, х3) называется нормальной, так как знак инверсии применяется только к аргументам, а не к функциям от них, и совершенной, так как каждый ее конъюнктивный член содержит все n аргументов.
. Полученная аналитическая запись f(x1, x2, х3) называется нормальной, так как знак инверсии применяется только к аргументам, а не к функциям от них, и совершенной, так как каждый ее конъюнктивный член содержит все n аргументов.
Обратный переход - от аналитического задания ФАЛ к табличному - выполняется следующим образом:
1) составляется таблица всех возможных наборов аргументов;
2) значения аргументов из каждого набора подставляют непосредственно аналитическую запись ФАЛ, и на основе определений элементарных ФАЛ вычисляется ее значение на каждом наборе;
3) вычисленное значение заносится в таблицу в строку, соответствующую рассмотренному набору.
Все три способа задания ФАЛ взаимно-однозначны. В каждом конкретном случае используются те способы, которые оказываются удобнее в этом случае.
Набор функций алгебры логики называется функционально полным, если любая ФАЛ может быть представлена суперпозицией этого набора. Функционально полный набор ФАЛ обычно называется базисом. Минимальным базисом называется такой базис, для которого удаление хотя бы одной из функций, образующих этот базис, лишает его функциональной полноты. Понятие полноты и минимального базиса, является фундаментальными понятиями алгебры логики, имеющими большое теоретическое и прикладное значение. Оказывается, для построения сложных ФАЛ достаточно иметь небольшой набор элементарных функций. Иными словами, устройства ЭВМ, работа которых, как известно, описывается системой ФАЛ, могут быть построены из ограниченного набора элементов, соответствующих некоторому базису. В математической логике разработаны категории полноты, позволяющие определить,является ли данный набор ФАЛ полным, и, следовательно, можно ли из данных элементов построить вычислительную машину или вообще любое устройство переработки дискретной информации, работа которого может быть описана на языке ФАЛ.
Аппарат алгебры логики позволяет не только находить минимальные наборы полных ФАЛ, но и производить преобразование сложных ФАЛ с целью минимизации количества элементарных базисных ФАЛ, составляющих заданную функцию.Применительно к технике это позволяет строить минимальные по количеству стандартных элементов схемы, способные выполнять требуемые функции.
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 325; Нарушение авторских прав?; Мы поможем в написании вашей работы!