Конечные автоматы

В большинстве случаев работа устройства в момент t_i определяется не только входным словом, подаваемым в момент времени t_i, но зависит также и от входных слов, поступивших в предыдущие моменты времени. В этом случае имеют дело с автоматом с памятью, который часто называют просто конечным автоматом. Конечные автоматы изучаются в теории автоматов разделе кибернетики.

Устройства, которые служат для преобразования дискретной информации, называются дискретными автоматами. Дискретную информацию задают алфавитом,буквы которого отождествляют с цифрами. Поэтому дискретные автоматы принято также называть цифровыми. Основным качеством, выделяющим дискретные автоматы из числа всех других преобразователей информации, является наличие дискретного (для реальных автоматов всегда конечного) множества внутренних состояний и свойства скачкообразного перехода автомата из одного состояния в другое. Скачкообразность перехода позволяет трактовать этот переход как мгновенный без промежуточных состояний. При этом переходные процессы не принимаются во внимание.

Считается также, что переход из одного состояния в другое оказывается возможным не ранее, чем через промежуток времени Dt>0. Это допущение позволяет рассматривать функционирование автомата в дискретном времени.

В синхронных автоматах моменты времени, в которые оказывается возможным изменение состояния автомата, определяются специальным устройством - генератором синхроимпульсов. В асинхронных автоматах моменты переходов из одного состояния в другое заранее не определены и совершаются через неравные промежутки времени. Теория асинхронных автоматов из-за этого отличается от теории синхронных автоматов.

Но можно свести ее в ряде случаев к теории синхронных автоматов, вводя понятие абстрактного автоматного времени: t=0, 1, 2,...n.

Общая теория автоматов делится на абстрактную и структурную теорию автоматов. В автомате имеются алфавиты: входной - X, выходной - У и состояний - А. Число входных сигналов конечно, и они рассматриваются как причина перехода из одного состояния в другое: a(t-1)®a(t), где аÎА. Число выходных сигналов конечно и каждому отличному от О моменту автоматного времени соответствует выходной сигнал y(t), который может появиться в момент t, но обязательно после входного сигнала x(t), соответствующего этому же моменту времени (уÎУ и хÎХ). У(t) может появиться в момент перехода из состояния a(t-1) в a(t) или после перехода. В первом случае y(t) однозначно определяется парой x(t) и a(t-1), во втором случае - парой x(t) и a(t). Поэтому различают автоматы I рода (автоматы Мили) и II рода (автоматы Мура).

Абстрактный автомат и способы его задания. Абстрактный автомат задается как совокупность шестерки объектов: конечного множества X входных сигналов (входной алфавит); конечного множества У выходных сигналов (выходной алфавит); множества А, называемого множеством состояний автомата; из множества А, называемого

начальным состоянием автомата и функций d(а, х) и l(а, х), задающих однозначное отображение множества пар а, х (аÎА и xÎX) в множества А и У. Функция d(а, х) называется функцией переходов автомата, а функция l(а, х) - функцией выходов, либо сдвинутой функцией выходов. Если автомат задан функцией выходов, то это автомат I рода (Мили), сдвинутой функцией выходов - II рода (Мура).

Для автомата Мили: a(t)=d(a(t-1)), х(t); У(1)=l(а(t-1)), х(t); (t= ).

Для автомата Мура: a(t)=d(a(t-1)), х(t); У(1)=l(а(t)), х(t)= l(а(t)); (t= ).

Существует несколько способов задания автоматов. Наиболее распространенными являются табличный и графический. При табличном способе задания автоматов описание работы автомата задается таблицей переходов и выходов. Таблицей 2.4 задана функция переходов а=d(а, х), а таблицей 2.5 задана функция выходов y=l(а, х) автомата Мили.

При графическом способе задания автоматов описание работы автомата задается в виде ориентированного связ­ного графа, вершины которого соответствуют состояниям автомата, а дуги - переходам между ними. Две вершины а_i и а_s графа автоматасвязаны между собой дугой, направленной от a_i к a_s, если в автомате имеется переход от a_i к а_s, т.е. а_s=d(а_i, x_j) при некотором x_jÎX. Дуге (a_i, а_s) графа автомата Мили приписывается входной сигнал x_j и выходной y_g=l(a_i, x_j), если он определен, в противном случае ставится прочерк (рис. 4.1). Граф автомата Мура отличается от графа автомата Мили тем, что выходной сигнал приписан вершине графа (Рис. 2.1).

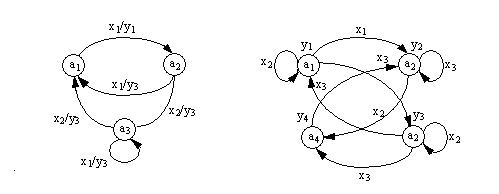
Рис. 2.1. Графическое изображение автомата

Основная литература: 2 [82-123],3 [51-82]

Дополнительная литература: 5 [236-283], 7 [305-361]

Контрольные вопросы:

1. Назовите основные способы задания ФАЛ?

2. Чем отличается ДСНФ от КСНФ?

3. Назовите основные методы минимизации ФАЛ?

4. Назовите отличе автомата Мура от автомата Миля?

5. Назовите основные формы представления автомата?

Дата добавления: 2014-01-04