Определение параметров линейного однофакторного уравнения регрессии

Пусть у нас имеются данные о доходах (x) и спросе на некоторый товар (y) за ряд лет (n):

Год i	Доход x	Спрос y
	x 1	y 1
	x 2	y 2
	x 3	y 3
...	...	...
n	x n	y n

Предположим, что между x и y существует линейная взаимосвязь, т.е.

.

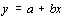Для того, чтобы найти уравнение регрессии, прежде всего нужно исследовать тесноту связи между случайными величинами x и y, т.е. корреляционную зависимость.

Пусть

x ₁ , x ₂ ,..., x _n совокупность значений независимого, факторного признака;

y ₁ , y ₂ ,..., y _n совокупность соответствующих значений зависимого, результативного признака;

n количество наблюдений.

Для нахождения уравнения регрессии вычисляются следующие величины:

1. Средние значения

для экзогенной переменной;

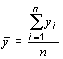для эндогенной переменной.

2. Отклонения от средних величин

, .

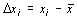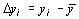3. Величины дисперсии и среднего квадратичного отклонения

, ;

, .

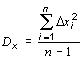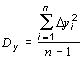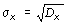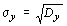Величины дисперсии и среднего квадратичного отклонения характеризуют разброс наблюдаемых значений вокруг среднего значения. Чем больше дисперсия, тем больше разброс.

4. Вычисление корреляционного момента (коэффициента ковариации):

.

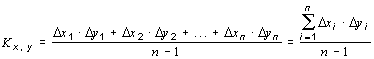Корреляционный момент отражает характер взаимосвязи между x и y. Если K _{x, y} > 0, то взаимосвязь прямая. Если K _{x, y} < 0, то взаимосвязь обратная.

5. Коэффициент корреляции вычисляется по формуле

.

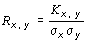Доказано, что коэффициент корреляции находится в интервале от минус единицы до плюс единицы (- 1 >= R _{x, y} <= 1). Коэффициент корреляции в квадрате 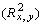называется коэффициентом детерминации.

Если R _{x, y} > |0,8|, то вычисления продолжаются.

6. Вычисления параметров регрессионного уравнения.

Коэффициент b находится по формуле

.

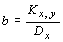После чего можно легко найти параметр a:

.

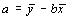Коэффициенты a и b находятся методом наименьших квадратов, основная идея которого состоит в том, что за меру суммарной погрешности принимается сумма квадратов разностей (остатков) между фактическими значениями результативного признака y _i и его расчетными значениями y _{i р} , полученными при помощи уравнения регрессии

.

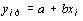При этом величины остатков находятся по формуле

,

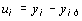где y _i фактическое значение y; y _{i р} расчетное значение y.

Дата добавления: 2014-01-04