Оценка величины погрешности линейного однофакторного уравнения

1. Обозначим разность между фактическим значением результативного признака и его расчетным значением как u _i :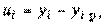

где y _i фактическое значение y; y _{i р} расчетное значение y; u _i разность между ними.

2. В качестве меры суммарной погрешности выбрана величина

.

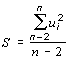Для нашего примера S = 0,432.

Поскольку 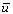(среднее значение остатков) равно нулю, то суммарная погрешность равна остаточной дисперсии.

3. Остаточная дисперсия находится по формуле

.

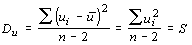Для нашего примера 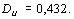Можно показать, что

.

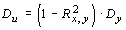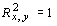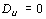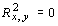Если , то ;

, то .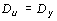

Таким образом, 0≥ D _u ≥ D _y .

Легко заметить, что если

то .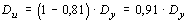

Это соотношение показывает, что в экономических приложениях допустимая суммарная погрешность может составить не более 20% от дисперсии результативного признака D _y .

4. Стандартная ошибка уравнения находится по формуле

,

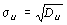где D _u остаточная дисперсия. В нашем случае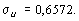

5. Относительная погрешность уравнения регрессии вычисляется как

,

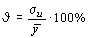где 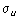стандартная ошибка; 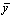среднее значение результативного признака.

В нашем случае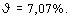

Если величина 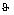мала и отсутствует автокорреляция остатков, то прогнозные качества оцененного регрессионного уравнения высоки.

6. Стандартная ошибка коэффициента b вычисляется по формуле

.

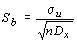В нашем случае она равна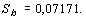

Для вычисления стандартной ошибки коэффициента a используется формула

.

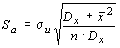В нашем примере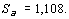

Стандартные ошибки коэффициентов используются для оценивания параметров уравнения регрессии.

Коэффициенты считаются значимыми, если

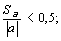
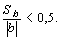
В нашем примере

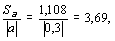
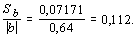
Коэффициент а не значим, так как указанное отношение больше 0,5, а относительная погрешность уравнения регрессии слишком высока 26,7%.

Стандартные ошибки коэффициентов используются также для оценки статистической значимости коэффициентов при помощи t -критерия Стьюдента. Значения t -критерия Стьюдента содержатся в справочниках по математической статистике. В таблице 2.1 приводятся его некоторые значения.

Далее находятся максимальные и минимальные значения параметров (b-, b ⁺ )по формулам:

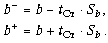
Таблица 2.1 – Некоторые значения t -критерия Стьюдента

Степени свободы	Уровень доверия (с)
(n- 2)	0,90	0,95
	6,31	12,71
	2,92	4,30
	2,35	3,18
	2,13	2,78
	2,02	2,57

Для нашего примера находим

,

.

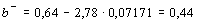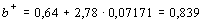Если интервал (b-, b ⁺ ) достаточно мал и не содержит ноль, то коэффициент b является статистически значимым на с -процентном доверительном уровне.

Аналогично находятся максимальные и минимальные значения параметр a. Для нашего примера

,

.

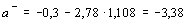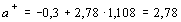Коэффициент а не является статистически значимым, так как интервал (a-, a ⁺ ) велик и содержит ноль.

Вывод: полученные результаты не являются значимыми и не могут быть использованы для прогнозных расчетов. Ситуацию можно поправить следующими способами:

а) увеличить число n;

б) увеличить количество факторов;

в) изменить форму уравнения.

Дата добавления: 2014-01-04