Многомерный и одномерный поиск оптимума

МСС представляет собой многомерный поиск, т.к. минимум ищется на разных направлениях. Когда минимум ищется только в одном направлении для уточнения направления следующего уровня - одномерный поиск.

Одномерный поиск

Для многомерного поиска разработаны десятки методов, для одного поиска около 1 десятка методов. Рассмотрим одномерное приближение.

Метод последовательных приближений

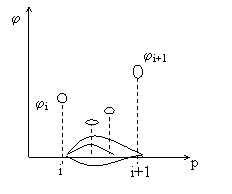
P - длина шага оптимизации;

φ - значение целевой функции

1. при нарушении условий движения (φi+1 > φi) движение останавливается

2. Возвращается на 1 шаг назад.

3. Делим длину шага на R где R = 3-10

4. Возобновляем движение с новым шагом.

5. При нарушении условий движения все повторяется, и т.д.

Условия останова:

- Значение j < заданного

- Разность между соседними значениями j < заданной

- Длина шага < заданной

- Кол-во шагов превышает заданное.

Любое из этих условий приводит к останову.

Метод золотого сечения

Если возьмем пропорцию:

x₁/x = x₂/x₁ = 0.618-m_o

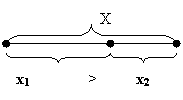
Такое соотношение называется золотой пропорцией.

1. При нарушении условий движения последний шаг делим в отношении золотой пропорции слева на право.

2. Этот же отрезок делим в золотой пропорции справа на лево. В результате получим 2 новые точки

3. Сравниваем значения j в новых точках.

4. Выбираем отрезок, которому соответствует меньшее из этих двух j.

5. Полученный отрезок делим в отношении золотой пропорции слева направо, и т.д.

Условия останова те же, что и в предыдущем случае.

Метод параболической аппроксимации (МПА)

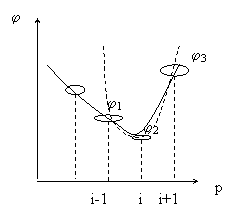
При нарушении условий значения j в последних 3-х точках подставляется в формулу решения системы 3-х уравнений для параболы. Это решение позволяет находить координаты минимума параболы, проходящий через 3 последние точки.

Сравнение методов одномерного поиска

МПП более прост (движемся, делим), но требует много шагов (м.б. 10 и 100 шагов).

МЗС позволяет найти min за 3-4 шага.

МПА более сложен, но позволяет найти min за 1 шаг. Но МПА обладает методической погрешностью, поскольку парабола отличается от истинной кривой; обычно эта погрешность невелика. В пакетах программ для расчета оптики обычно используется в качестве метода многомерного поиска демнорированый МСС, а в качестве метода одномерного поиска - МПА.

Дата добавления: 2014-01-04