Понятие оптимизационных задач и оптимизационных моделей

Оптимизационные модели

Экономико-математические задачи, цель которых состоит в нахождении наилучшего (оптимального) с точки зрения некоторого критерия или критериев варианта использования имеющихся ресурсов (труда, капитала и пр.), называются оптимизационными.

Оптимизационные задачи (ОЗ) решаются с помощью оптимизационных моделей (ОМ) методами математического программирования.

Структура оптимизационной модели состоит из целевой функции, области допустимых решений и системы ограничений, определяющих эту область. Целевая функция в самом общем виде, в свою очередь, также состоит из трех элементов:

o управляемых переменных;

o неуправляемых переменных;

o формы функции (вида зависимости между ними).

Область допустимых решений это область, в пределах которой осуществляется выбор решений. В экономических задачах она ограничена наличными ресурсами, условиями, которые записываются в виде системы ограничений, состоящей из уравнений и неравенств.

Если система ограничений несовместима, то область допустимых решений является пустой. Ограничения подразделяются:

а) на линейные (I и II) и нелинейные (III и IV) (рис. 3.1);

б) детерминированные (А, В) и стохастические (группы кривых С _i ) (рис. 3.2).

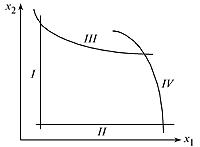Рисунок 3.1– Линейные и нелинейные ограничения

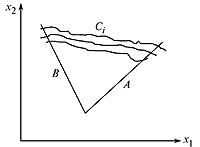Рисунок 3.2– Детерминированные и стохастические ограничения

Стохастические ограничения являются возможными, вероятностными, случайными.

ОЗ решаются методами математического программирования, которые подразделяются:

o на линейное программирование;

o нелинейное программирование;

o динамическое программирование;

o целочисленное программирование;

o выпуклое программирование;

o исследование операций;

o геометрическое программирование и др.

Главная задача математического программирования это нахождение экстремума функций при ограничениях в форме уравнений и неравенств.

Рассмотрим ОЗ, решаемые методами линейного программирования.

Дата добавления: 2014-01-04